Урок алгебры 8 класс на тему Квадратные уравнения

Урок по алгебре с применением стратегии развития критического мышления

Учиться вместе, а не просто

что-то выполнять вместе —

вот суть данного подхода.

Воскресеновская сш

учитель математики

Осадчая О.А .

Технология РКМ:

• Формирует самостоятельное мышление
• Вооружает методами и способами самостоятельной работы
• Даёт возможность сознательно управлять образовательным процессом в системе “учитель-ученик”
• Позволяет влиять на результат и цели образовательного процесса

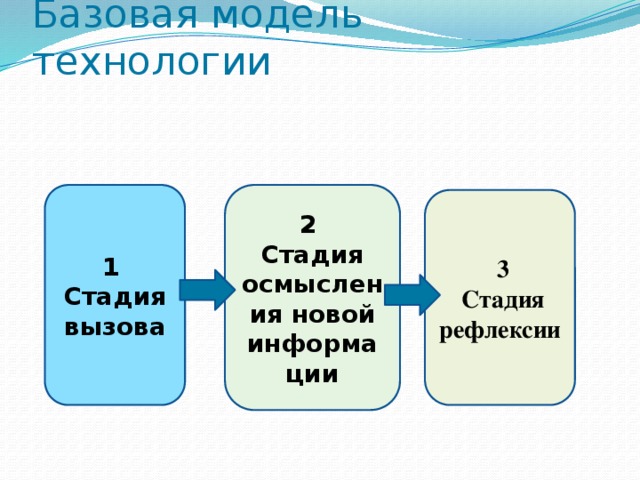
Базовая модель технологии

1

2

Стадия вызова

Стадия осмысления новой информации

3

Стадия рефлексии

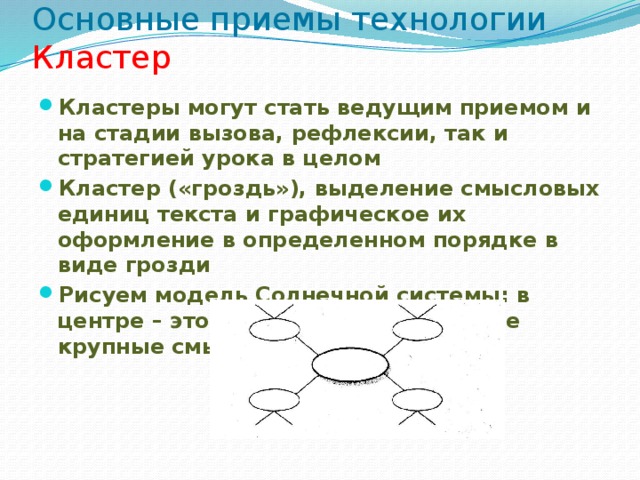
Основные приемы технологии Кластер

• Кластеры могут стать ведущим приемом и на стадии вызова, рефлексии, так и стратегией урока в целом
• Кластер («гроздь»), выделение смысловых единиц текста и графическое их оформление в определенном порядке в виде грозди
• Рисуем модель Солнечной системы: в центре – это наша тема, а вокруг нее крупные смысловые единицы

Рекомендации по работе с «гроздями»:

• Оцените текст, с которым будете работать. Нужна ли в данном случае разбивка на «грозди»?
• Помогите ученику, если у него возникли сомнения при выделении смысловых единиц.
• Озвучьте свои «грозди». Пусть ученики сделают презентацию своих записей.
• Попросите установить связи между «веточками» вашей «грозди» и объяснить возникшие связи.
• Если вы хотите остановиться на каком-либо смысловом блоке, попросите сделать эту «веточку» поярче.

Основные приемы технологии Инсерт

• Чтение текста с пометками:     + я это знал,     - я этого не знал,     ! это меня удивило     ? хотел бы узнать подробнее.
•   Составление таблицы, выписываются основные положения из текста

+

-

!

?

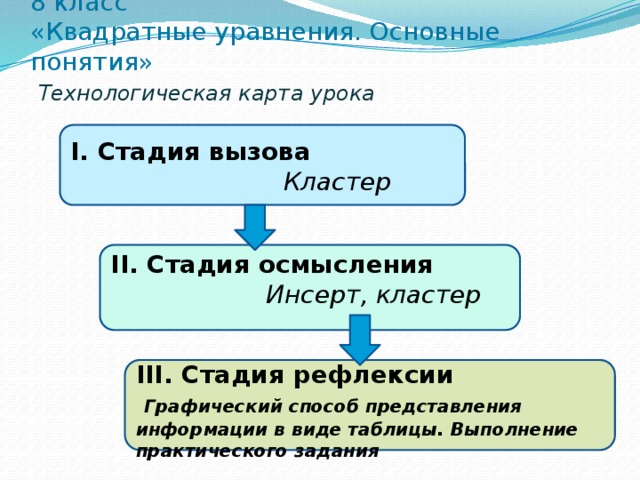
8 класс «Квадратные уравнения. Основные понятия» Технологическая карта урока

I. Стадия вызова

Кластер

II. Стадия осмысления

Инсерт, кластер

III. Стадия рефлексии

Графический способ представления информации в виде таблицы. Выполнение практического задания

Стадия вызова

Работа с текстом

Задание: 1. Из данных уравнений выберите квадратные

1) x 2 – 2 =0; 2) x 3 +9x- 4=0; 3 ) 5x 2 - 4=0;

4) 6x=0; 5) x 2 – 2x +7=0; 6) 7x – x 2 + 3=0 .

2.Прочитайте п.24 стр.133 учебника, найдите определения

• полного и неполного квадратного уравнения
• приведенного и не приведенного квадратного уравнения
• корня квадратного уравнения

3. Изобразите информацию в виде

графического приема «гроздья»

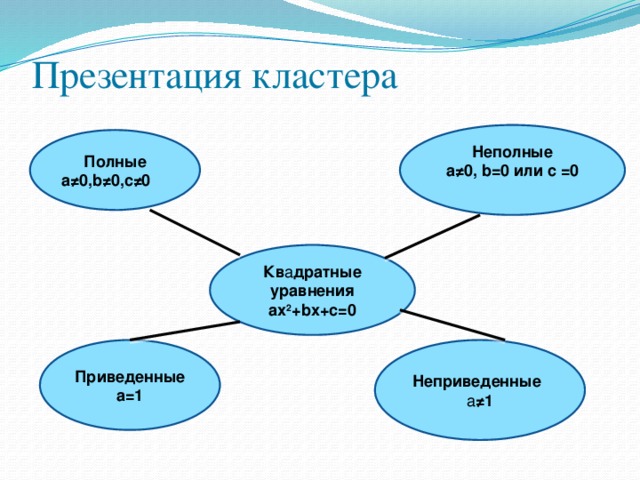
Презентация кластера

Неполные

a≠0, b=0 или с =0

Полные

а≠0,b≠0,c≠0

Кв а дратные уравнения

ax 2 +bx+c=0

Приведенные а=1

Неприведенные

а ≠1

Решение неполных квадратных уравнений

• ax 2 =0
• ax 2 +bx=0
• ax 2 +c=0

Чтение текста с пометками:     + я это знал     - я этого не знал     ! это меня удивило     ? хотел бы узнать подробнее

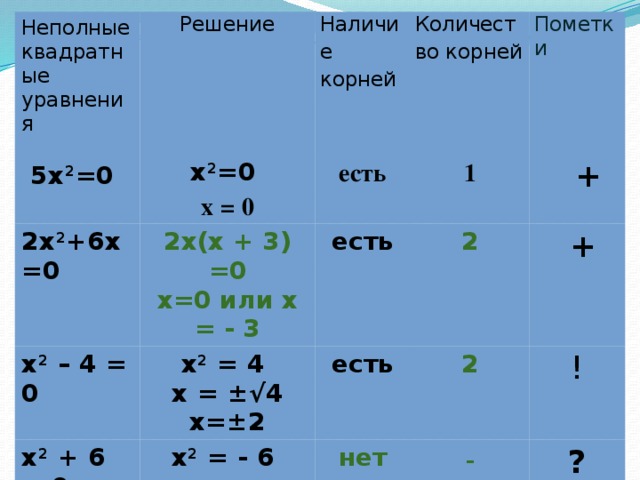
Неполные квадратные

5x 2 =0

Решение

уравнения

Наличие корней

2x 2 +6x=0

x 2 =0

2x(x + 3) =0

есть

Количество корней

x 2 – 4 = 0

x = 0

Пометки

есть

x 2 + 6 = 0

1

x 2 = 4

x=0 или x = - 3

2

x 2 = - 6

    +

есть

x = ±√4

нет

  +

x=±2

2

!

-

  ?

Веселая

зарядка

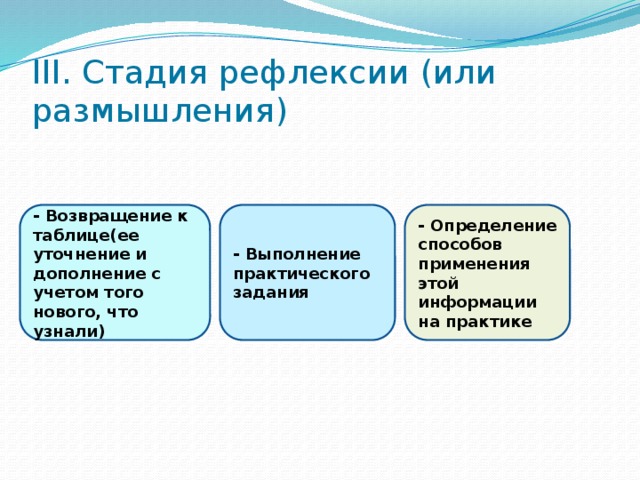
III. Стадия рефлексии (или размышления)

- Возвращение к таблице(ее уточнение и дополнение с учетом того нового, что узнали)

- Выполнение практического задания

- Определение способов применения этой информации на практике

0, то x 2 = - a/b - x 1 , 2 = ±√-c/a корней нет 2 x 1,2 = ±√- c/a" width="640"

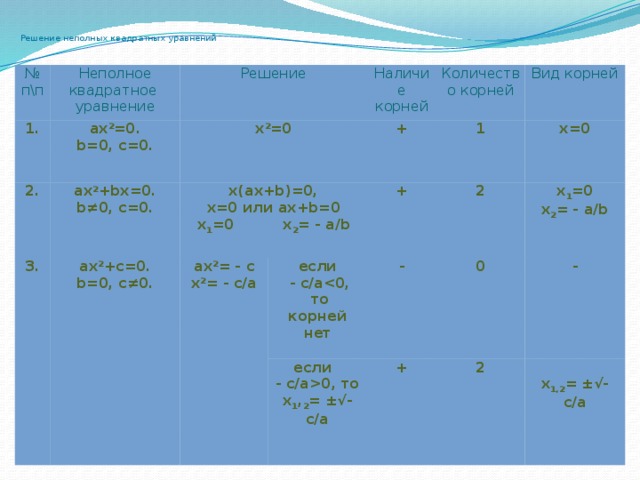
Решение неполных квадратных уравнений

№

п\п

Неполное

1.

аx 2 =0.

квадратное

Решение

2.

x 2 =0

b=0, с=0.

ax 2 +bx=0.

уравнение

3.

Наличие корней

x(ax+b)=0,

b≠0, с=0.

ax 2 +c=0.

x=0 или ax+b=0

Количество корней

+

b=0, с≠0.

ax 2 = - c

1

x 1 =0 x 2 = - a/b

+

Вид корней

если

x 2 = - c/a

2

x=0

если

- c/a

-

x 1 =0

то

+

0

- c/a0, то

x 2 = - a/b

-

x 1 , 2 = ±√-c/a

корней нет

2

x 1,2 = ±√- c/a

Разбейте следующие уравнения на две группы по какому-либо признаку:

1) 3х²+8х-7=0

7) 3х 2 – 5х – 4 =0

2) х 2 + 3х+ 1 = 0

8) х 2 - 24x = 0

3) 7-5х+х²=0

9) 16х 2 – 4 = 0

4) 5х 2 = 0

10) – 0,1х 2 + 10 = 0

5) 169 –х 2 = 0

11) - x 2 – 3x + 15 = 0

6) 7х + 13 -6х²=0

12) x 2 – 5x = 0

Приведенные и неприведенные

Неприведенные

• 3х²+8х-7=0
• - x 2 – 3x + 15 = 0

Приведенные

• х 2 + 3х+ 1 = 0
• 7-5х+х²=0

Приведенные и неприведенные

Неприведенные

• 3х²+8х-7=0
• - x 2 – 3x + 15 = 0

Приведенные

• х 2 + 3х+ 1 = 0
• 7-5х+х²=0

Полные и неполные

Полные

Неполные

• 1) 3х²+8х-7=0
• 2) х 2 + 3х+ 1 = 0
• 3) 7-5х+х²=0
• 7х + 13 -6х²=0
• 3х 2 – 5х – 4 =0
• - x 2 – 3x + 15 = 0

• 5х 2 = 0
• 169 –х 2 = 0
• х 2 - 24x = 0
• 16х 2 – 4 = 0
• – 0,1х 2 + 10 = 0
• x 2 – 5x = 0

Проверка

1) 5х 2 = 0 4) 16х 2 – 4 = 0

2) 169 –х 2 = 0 5) – 0,1х 2 + 10 = 0

3) х 2 - 24x = 0 6) x 2 – 5x = 0

0 и 5

А

10 и -10

К

13 и -13

В

0

Э

0,5 и -0,5

И

0 и 24

Р

Итог урока:

• “ Эврика” крикнул Архимед, когда открыл известный вам закон.
• Что вы открыли для себя сегодня?
• Что вы узнали нового?
• Домашнее задание: п24; №24.4а), №24.8б), №24.9а), 24.12а), №24.16б), 24.18б), 24.20б)

 

 

Литература:

• А.Г. Мордкович «Алгебра 7» учебник 1 часть
• А.Г. Мордкович «Алгебра 7»задачник 2 часть
• С.И. Заир-Бек, И.В. Муштавинская

«Развитие критического мышления на уроке»

• «Электронная зарядка» - http://galina27.ucoz.ru/index/0-17