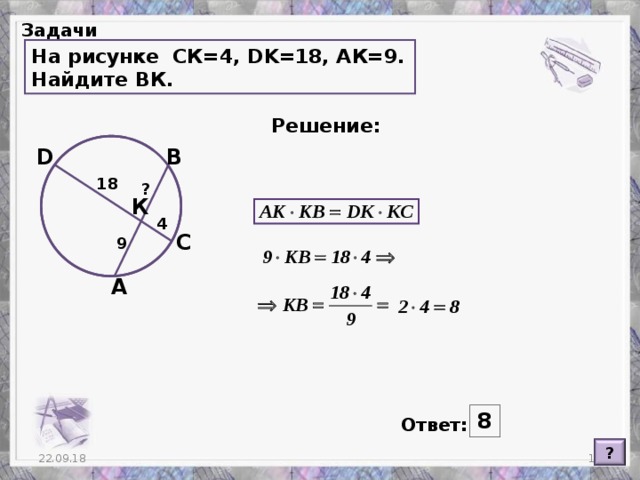
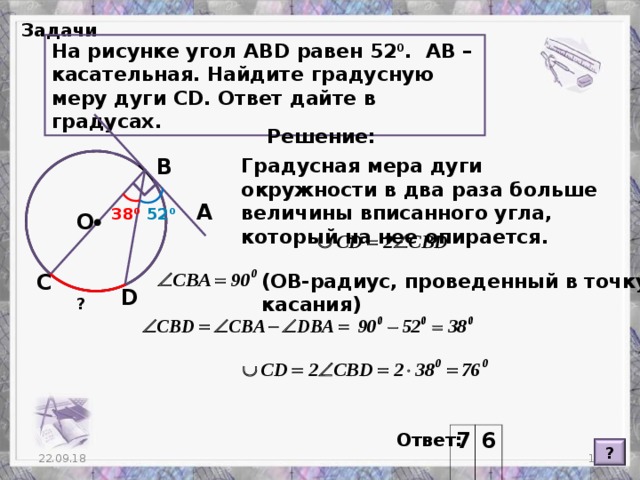
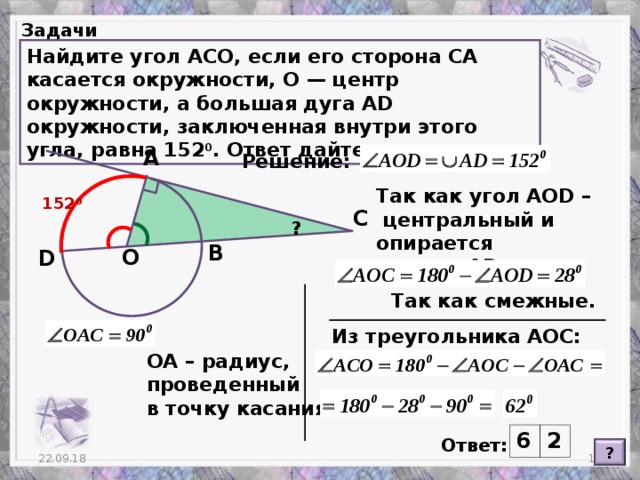
В ресурсе визуализирован весь основной теоретический материал по данной теме. Пошагово разобраны несколько задач. Можно использовать на уроках при изучении темы и для подготовки к экзамену.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
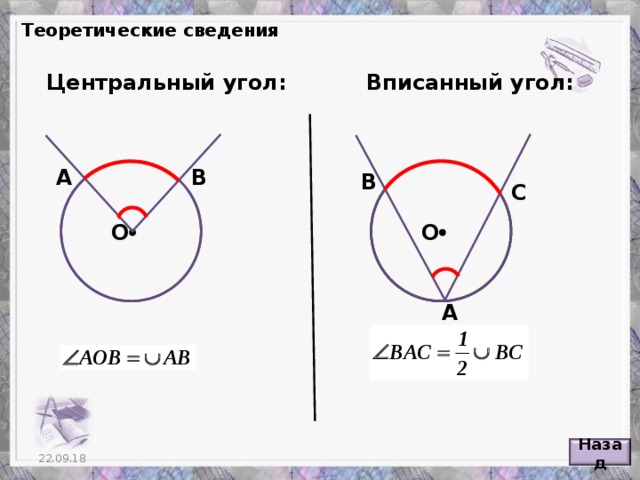
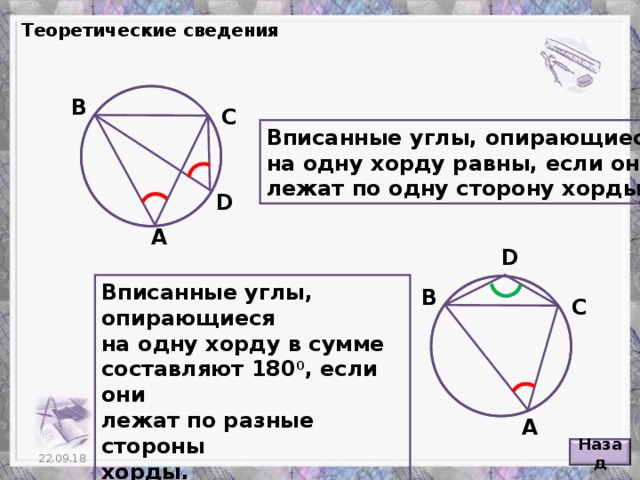
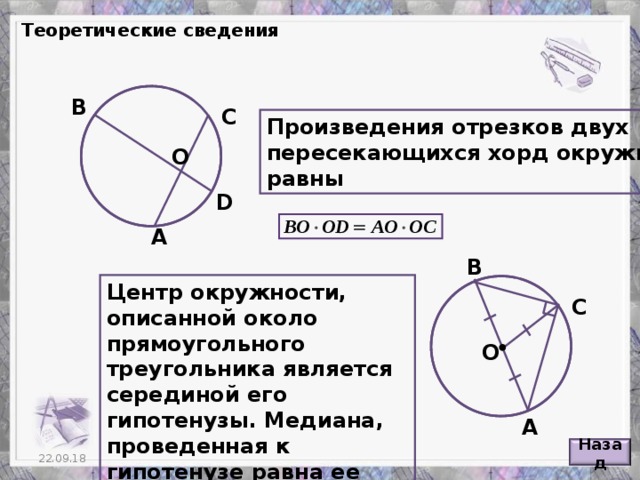
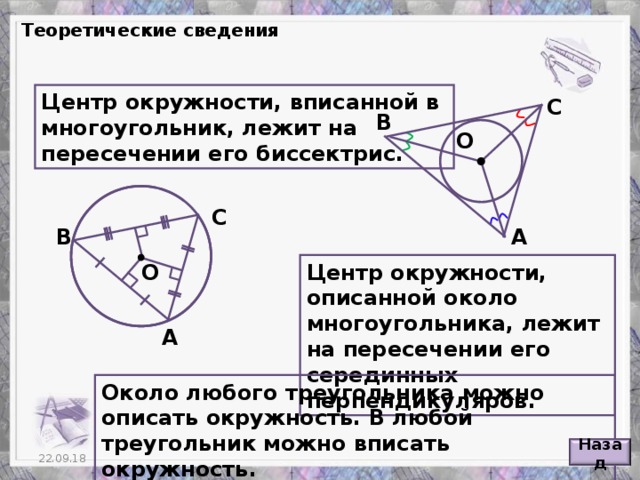
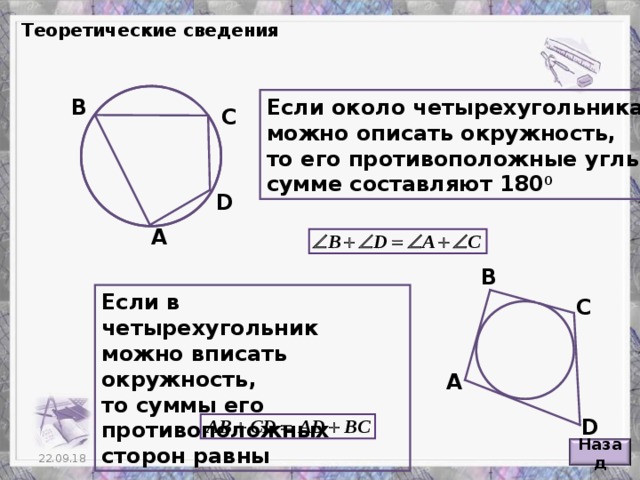
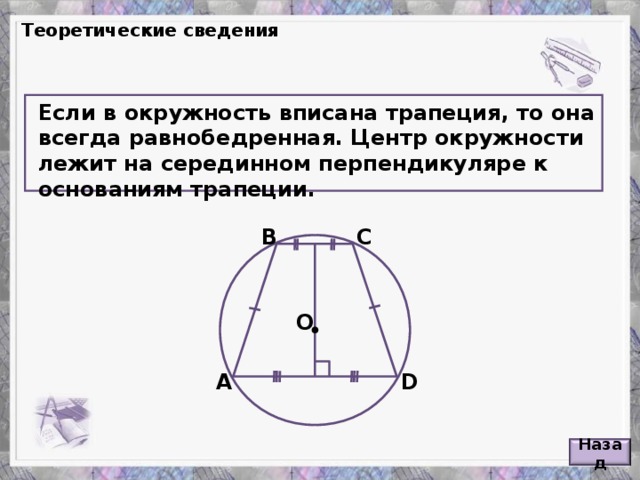
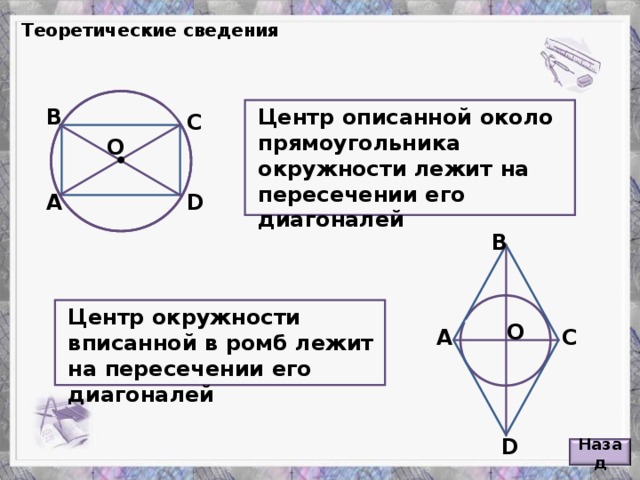
Углы в окружностях
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Углы в окружностях»
Полезное для учителя
Распродажа видеоуроков!
1490 руб.
2480 руб.
1800 руб.
3000 руб.
1800 руб.
3000 руб.
1400 руб.
2330 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

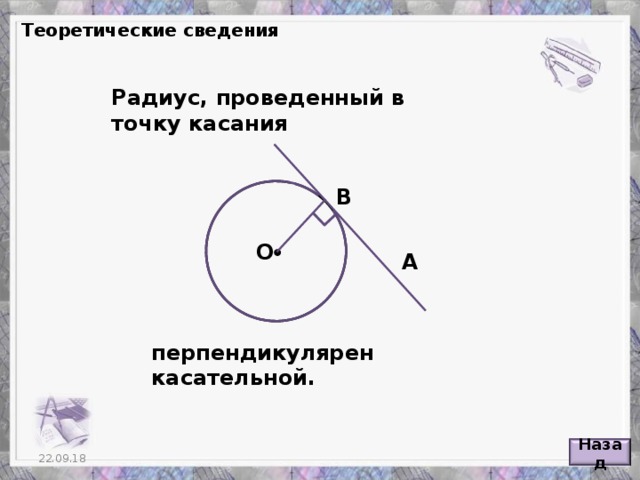
 = ОН – его медиана Из треугольника ОВН: 9 Ответ: 9 22.09.18" width="640"
= ОН – его медиана Из треугольника ОВН: 9 Ответ: 9 22.09.18" width="640"