Архив содержит конспект урока и презентацию по теме "теорема о вписанном угле"
Тема урока: «Теорема о вписанном угле». 8 класс
Цели урока:
Образовательные:
· Дать определение вписанного угла; научить распознавать вписанные углы на чертежах; предвидеть дополнительное построение, содержащее вписанный угол, ведущее к решению задачи;
· рассмотреть теорему о вписанном угле и следствия из нее; применять их при решении задач.
Развивающие:
· развивать логическое и пространственное воображение, интуицию учащихся;
· формировать умения чётко и ясно излагать свои мысли;
· совершенствовать графическую культуру.
Воспитательные:
· воспитывать умение работать с имеющейся информацией в необычной ситуации;
· воспитывать уважение к предмету.
Тип урока: изучение нового материала.
Форма урока: комбинированный.
Формы организации учебной деятельности: коллективная, индивидуальная.
Оборудование, наглядность, электронные приложения к уроку:
· Компьютер, беспроводная мышь. Мультимедийный проектор.
· Презентация Microsoft PowerPoint.
Структура урока
1. Организационный момент. Постановка цели урока.(1)
2. Повторение материала. Актуализация знаний.(3)
3. Введение определения вписанного угла. Отработка понятия на конкретных примерах.(3)
4. Подведение учащихся к самостоятельной формулировке теоремы. (3)
5. Доказательство теоремы.(6)
6. Подведение к самостоятельной формулировке следствий 1 и 2 из теоремы о вписанном угле путем создания и разрешения проблемной ситуации.(7)
8. Решение задач.(19)
9. Подведение итога урока.(4)
10. Домашнее задание.(2)
Ход урока
1. Организационный момент. Сообщение темы и цели урока.
Демонстрация презентации. (Слайд1)
Учитель сообщает тему урока и создает некоторую интригу, говорит, что сегодня на уроке необходимо выполнить большой объем работы: изучить теорему, два следствия из нее, решить несколько задач, в том числе и тех которые есть в ОГЭ.
2. Повторение материала. Актуализация знаний.
Вопросы:
· Какой угол называется центральным?
· Каким соотношением связаны центральный угол и дуга, на которую он опирается?
· Дайте определение внешнего угла треугольника.
· Какая теорема выражает его свойство?
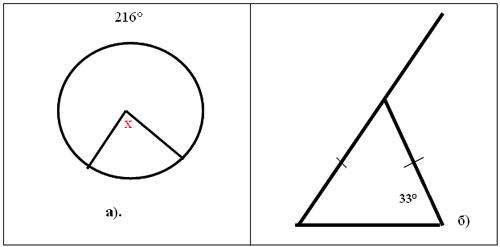
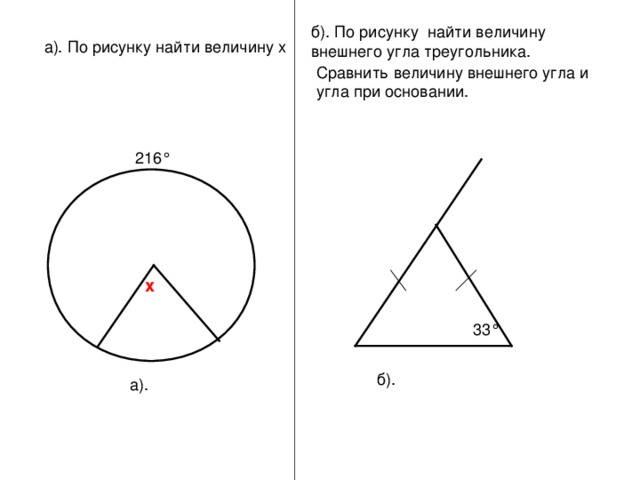
Задачи: (Слайд 2)
· По рисунку а). найти величину центрального угла, если величина большей дуги равна 216°.
· По рисунку б). найти величину внешнего угла.
Сравнить величину внешнего угла с углом при основании.
3. Введение определения вписанного угла. Отработка понятия на конкретных примерах.
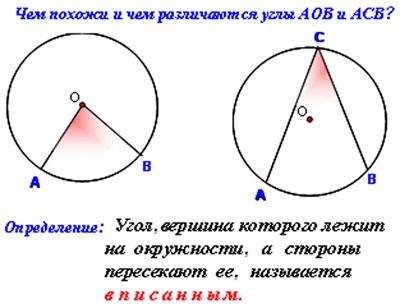
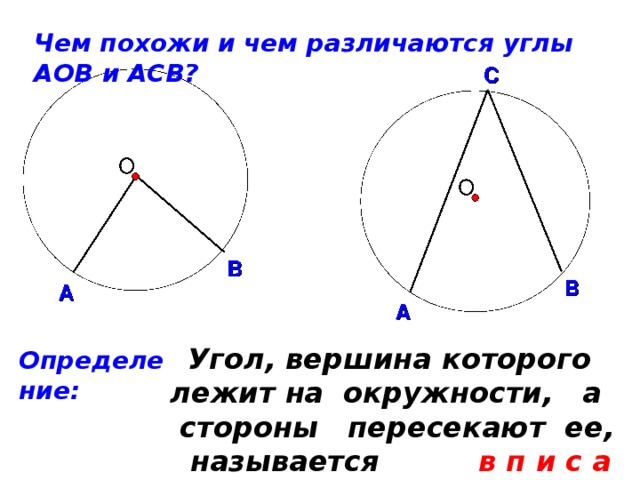
Работа со слайдом 3.
Вопрос: Чем похожи и чем отличаются углы АОВ и АСВ?
После ответа на этот вопрос учащиеся пытаются дать определение вписанного угла, после чего учитель выводит на экран формулировку, подчеркивая важные моменты:
· вершина лежит на окружности,
· стороны пересекают окружность.
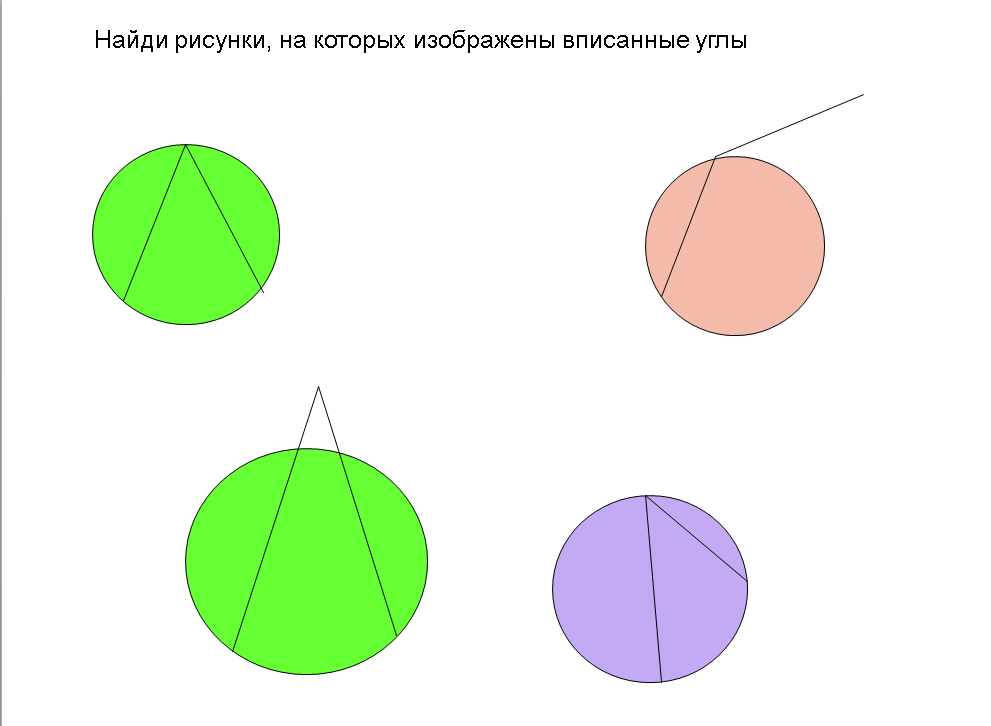
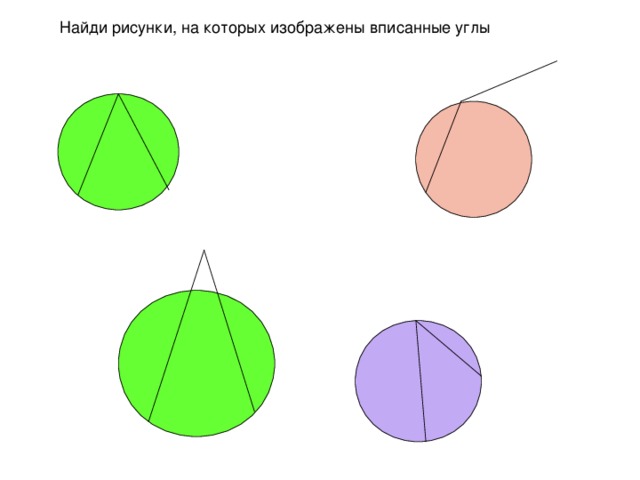
Работа со слайдом3 на закрепление понятия вписанного угла. Фронтальная работа с классом. Учащиеся определяют, является ли угол вписанным с пояснением (через формулировку определения)
4. Подведение учащихся к самостоятельной формулировке теоремы.
Задание: Выразить величину вписанного угла, зная, как выражается величина центрального угла через дугу, на которую он опирается.
Работа с слайдом 6-7
Какое дополнительное построение нужно сделать, чтобы выполнить указанное задание? Если учащиеся сразу не догадаются, уточнить: какой центральный угол нужно связать с данным вписанным углом?
Далее учащиеся видят, что полученный центральный угол является внешним углом равнобедренного треугольника и приходят к выводу, что один из углов (в частности вписанный), равный их полусумме, равен половине центрального, т.е. половине дуги, на которую он опирается.
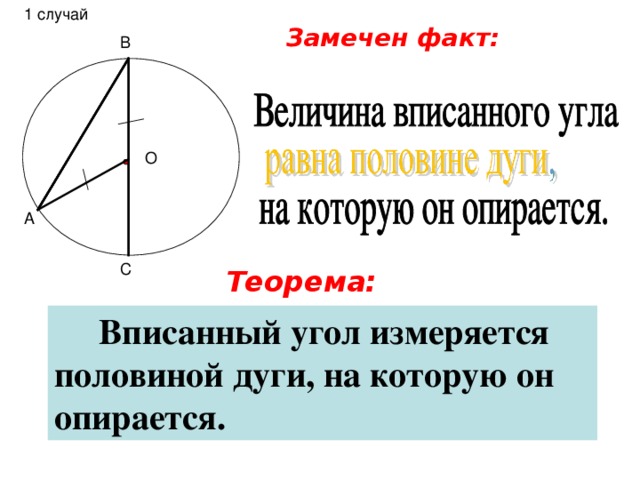
Далее учитель подтверждает замеченный ими факт, и говорит, что по сути дела в данном случае доказана теорема, которую нужно формулировать точно в соответствии с учебником.
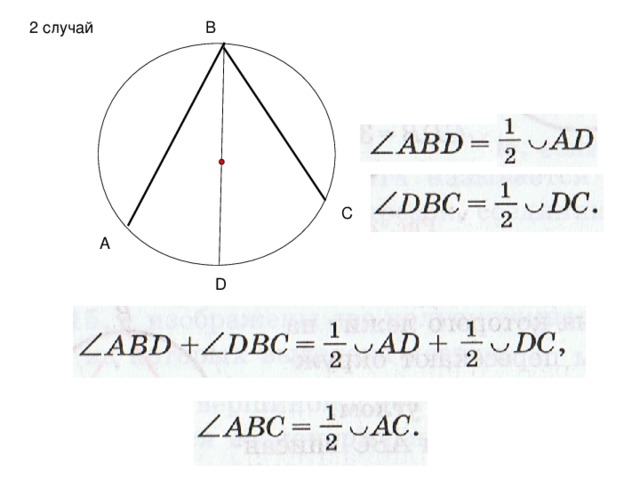
5. Доказательство теоремы.
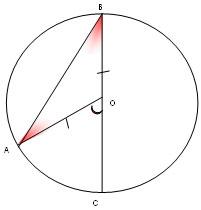
Дается точная формулировка теоремы и проецируется на экран. Ученики в тетрадь переносят чертеж, полученный на слайде 8, далее записывают в тетради условие. Один из учащихся комментирует записи. После чего анимируется слайд 8 с записью условия для проверки правильности, выполненных учащимися записей. Далее следующий ученик записывает и комментирует доказательство теоремы. Таким образом, полностью оформлено доказательство теоремы для случая, когда сторона вписанного угла проходит через центр окружности.
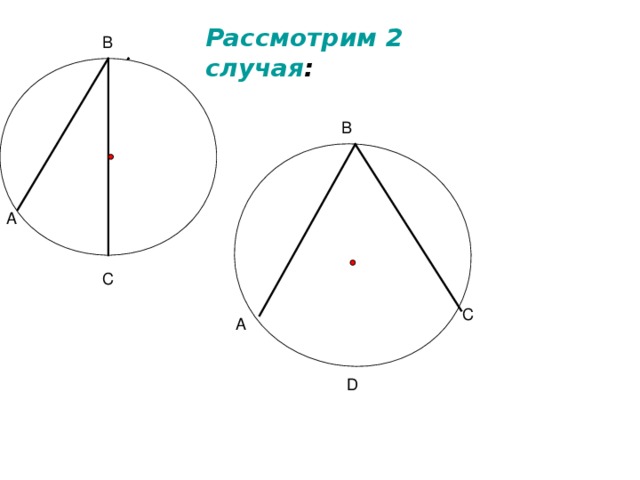
Случай, когда центр окружности лежит внутри угла, рассматривается устно с применением слайда 9.
Следующий случай, когда центр окружности лежит вне угла, учитель предлагает обосновать самостоятельно при домашней подготовке.
6. Подведение к самостоятельной формулировке следствий 1 и 2.
На доске чертеж.
Задание: отметить точку В, так чтобы получился вписанный угол. Учащиеся делают задание в тетрадях, потом к доске приглашаются 2-3 ученика для переноса своего чертежа на доску. Учащиеся формулируют 1 следствие «Вписанные углы, опирающиеся на одну и ту же дугу, равны».
Задание: Дана окружность, АС-диаметр, построить вписанный угол АВС. Найти его градусную меру.
Учащиеся формулируют 2-ое следствие «Вписанный угол, опирающийся на полуокружность – прямой»
7. Решение задач.
Цель этого этапа урока научить учащихся распознавать на чертежах вписанные углы, им соответствующие дуги, углы, опирающиеся на одни и те же дуги, равные углы, я называю это «всматриваться» в чертеж, в связи с этим задачи, за исключением второй, решаем устно.
Начало этого этапа, вводная беседа учителя, идет на фоне заставки «Решение задач» (Слайд 22).
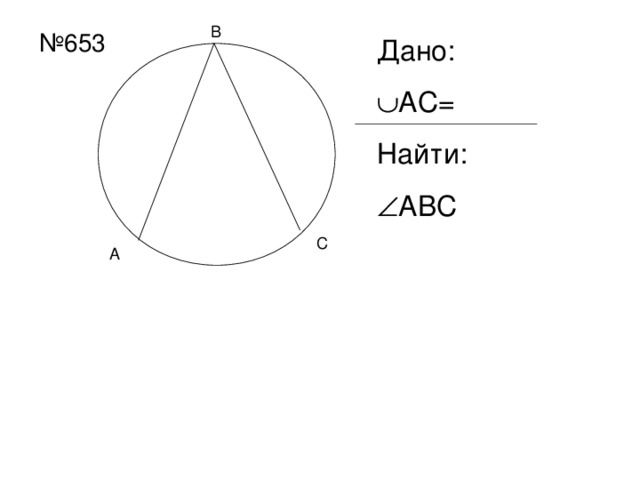
Задача 1.
(№653 учебника).
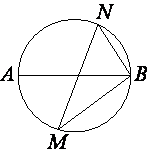
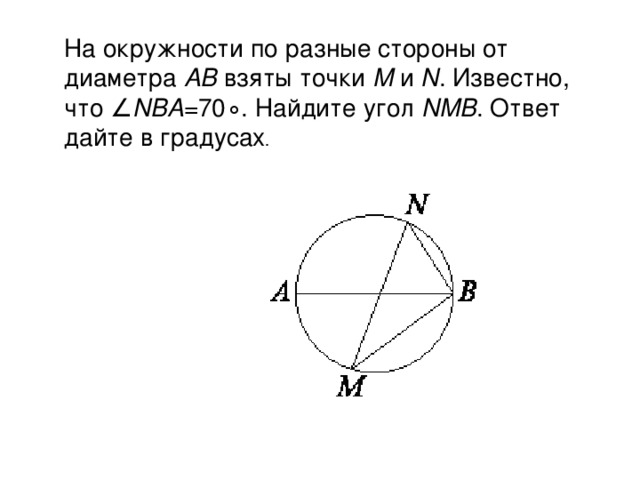
Задача 2. Слайд 12. Задачу по готовому чертежу письменно решают самостоятельно после того, как коллективно ее проанализируют.
Вопросы учителя классу:
· Как называется угол, который нужно найти?
· Что для этого нужно знать?
· Как называется угол АBN?
· На какую дугу опирается угол АBN?
· Как связаны дуги AN и NB?
Учащиеся коротко записывают решение в тетради.
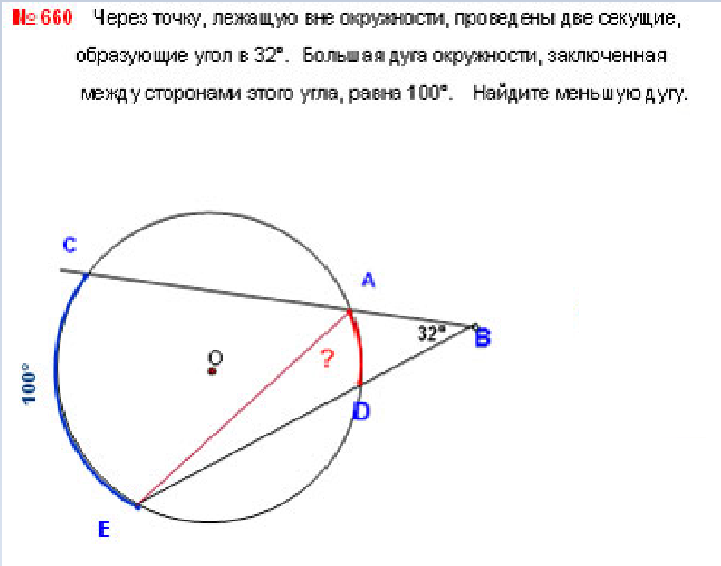
Задача 3. (№660 учебника). Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 32°. Большая дуга окружности, заключенная между сторонами этого угла, равна 100°. Найдите меньшую дугу.
Непросто догадаться сделать дополнительное построение, поскольку учащиеся еще не привыкли «видеть» вписанные углы, то есть те углы, которые появляются в результате дополнительного построения
Задачу решаем устно.
9. Подведение итога урока.
Для подведения итога урока учащиеся отвечают на вопросы слайда 13, помогающие понять степень осознания изученного материала.
Задание 1:
Найдите ошибку в формулировках:
· Вписанным называется угол, вершина которого лежит на окружности.
· Вписанный угол измеряется величиной дуги, на которую он опирается.
Закончите фразу:
· Вписанные углы равны, если…
· Вписанный угол прямой, если…
10. Домашнее задание
· п. 71, выучить определение вписанного угла,
· теорему о вписанном угле, (записав док-во 3 случая) и два следствия из нее,
· №657 – выполнить письменно,
· №654 – устно.
Список литературы:
1. Геометрия: Учеб. Для 7–9 кл. общеобразов. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.– М.: Просвещение, 2014 г.