"Теорема Пифагора" презентация к уроку геометрии

Теорема Пифагора

Пребудет вечной истина, как скоро

Её познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далёкий век .

Содержание

• Формулировка теоремы

• Доказательства теоремы
• Значение теоремы Пифагора

Формулировка теоремы

Во времена Пифагора теорема звучала так:

• « Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»

• « Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». 

или

Современная формулировка

« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».    

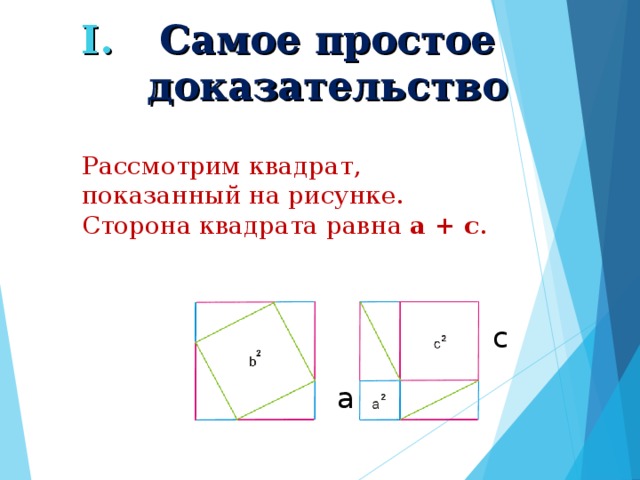
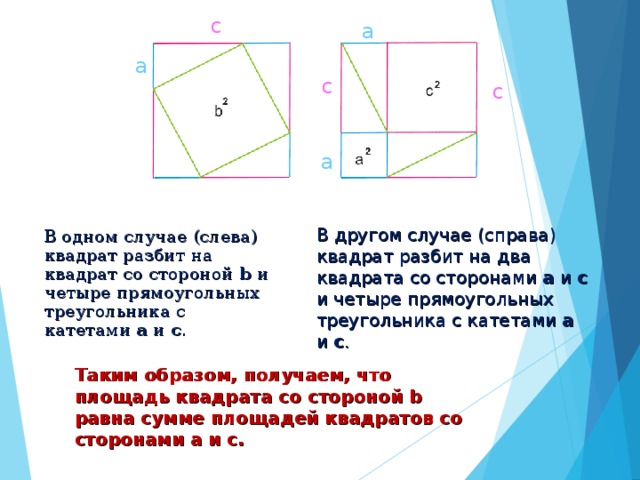
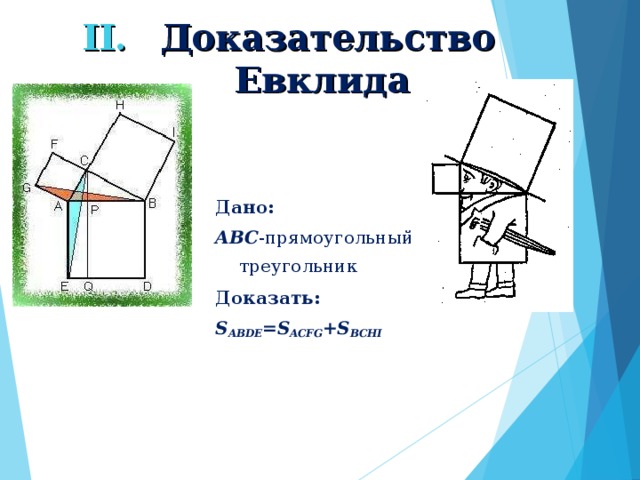
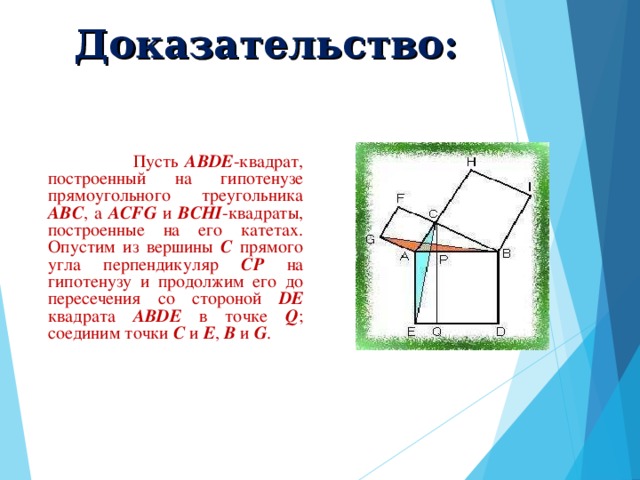
Доказательства теоремы

Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).

• Самое простое доказательство

Рассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c .

c

a

c

a

a

c

c

В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c .

a

В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c .

Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.

• Доказательство Евклида

Дано:

ABC -прямоугольный треугольник

Доказать:

S ABDE =S ACFG +S BCHI

Доказательство:

Пусть ABDE -квадрат, построенный на гипотенузе прямоугольного треугольника ABC , а ACFG и BCHI -квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q ; соединим точки C и E , B и G .

Очевидно, что углы CAE=GAB(=A+90°) ; отсюда следует, что треугольники ACE и AGB (закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA ; они имеют общее основание AE и высоту AP , опущенную на это основание, следовательно

S PQEA = 2S ACE

Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, S FCAG =2S GAB

Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.

• Алгебраическое доказательство

Дано: ABC -прямоугольный треугольник

Доказать: AB 2 =AC 2 +BC 2

  Доказательство:

1) Проведем высоту CD из вершины прямого угла С . 2) По определению косинуса угла соsА=AD/AC=AC/AB , отсюда следует

AB*AD=AC 2 .

3) Аналогично соsВ=BD/BC=BC/AB , значит

AB*BD=BC 2 .

4) Сложив полученные равенства почленно, получим:

AC 2 +BC 2 = АВ *(AD + DB)

AB 2 =AC 2 +BC 2 . Что и требовалось доказать.

• Геометрическое доказательство

Дано: ABC -прямоугольный треугольник

Доказать: BC 2 =AB 2 +AC 2

Доказательство:

1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC . Затем опустим перпендикуляр ED к отрезку AD , равный отрезку AC , соединим точки B и E . 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:

S ABED =2*AB*AC/2+BC 2 /2

3) Фигура ABED является трапецией, значит, её площадь равна:

S ABED = (DE+AB)*AD/2.

4) Если приравнять левые части найденных выражений, то получим:

AB*AC+BC 2 /2=(DE+AB)(CD+AC)/2

AB*AC+BC 2 /2= (AC+AB) 2 /2

AB*AC+BC 2 /2= AC 2 /2+AB 2 /2+AB*AC

BC 2 =AB 2 +AC 2 .

    Это доказательство было опубликовано в 1882 году Гэрфилдом.

Значение теоремы Пифагора

Теорема Пифагора- это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии .