Презентация
.
Происхождение систем счисления
Теории происхождения чисел
Вычисления в Древнем Египте
Вычисления в Вавилоне
Вычисления в Древнем Риме
- Запишите римскими числами ответы на следующие вопросы:
Появление арабских цифр
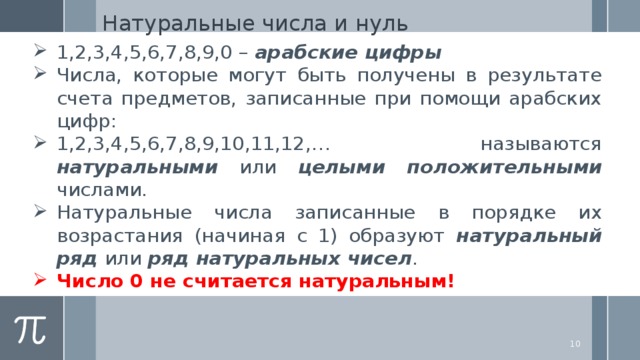
Натуральные числа и нуль
Натуральные числа и нуль
Строение натурального числа
Чтение натуральных чисел
Наименование натуральных чисел