nТеорема Пифагора имеет богатую историю. Оказывается, она задолго до Пифагора была известна египтянам, вавилонянам, китайцам и индийцам. За восемь веков до нашей эры эта теорема была хорошо известна индийцам под названием «правила веревки» и использовалась ими для построения алтарей, которые по священному предписанию должны иметь строгую геометрическую форму, ориентированную относительно четырех сторон горизонта. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель – моралист Плутарх, математик V века Прокл и другие.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
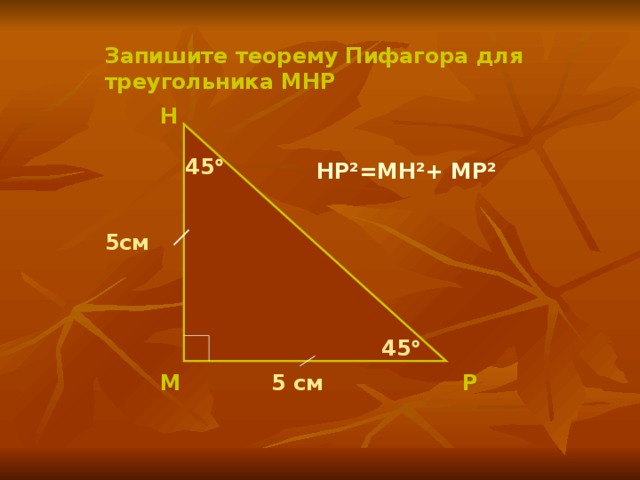
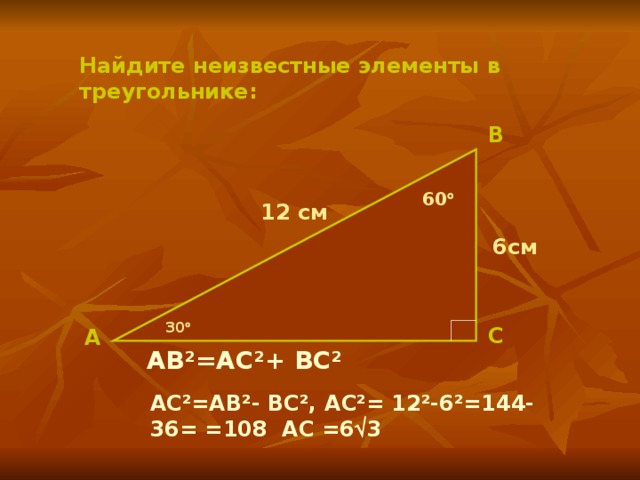
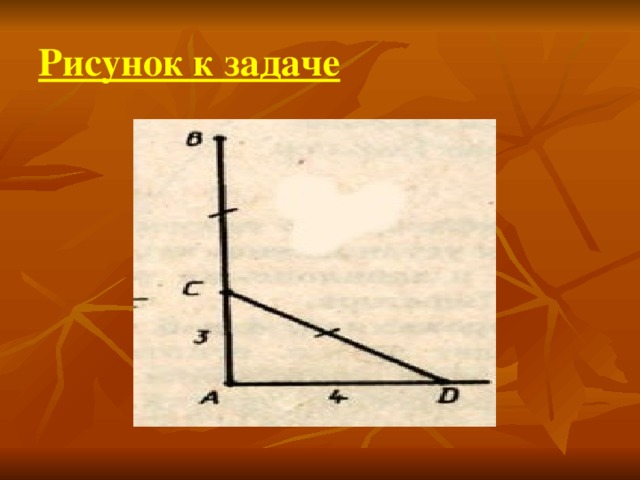
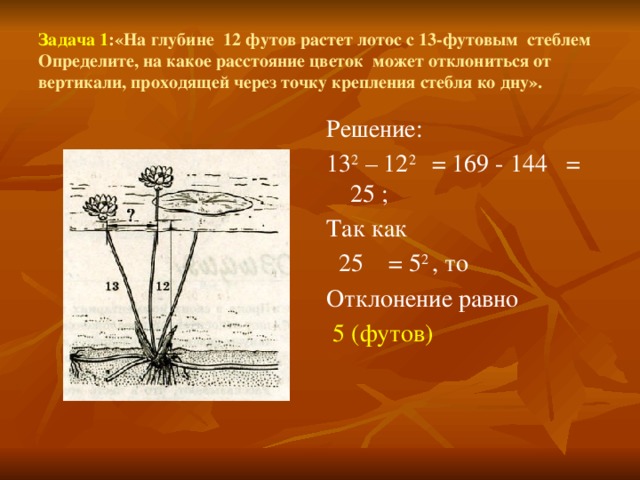
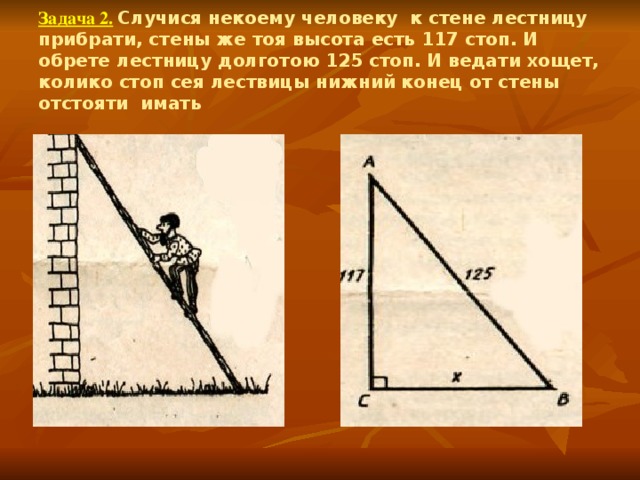
Решение задач по теореме Пифагора
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение задач по теореме Пифагора»
Полезное для учителя
Распродажа видеоуроков!
2020 руб.
2880 руб.
2000 руб.
2860 руб.
1970 руб.
2820 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства