Данная презентация представлена к теме: " Решение тригонометрических уравнений и неравенств", в ней представлены решения простейших тригонометрических уравнений, неравенств. Приведены примеры решения уравнений и неравенств на тригонометрической окружности, примеры для самостоятельной работы. Материал расчитан на учащихся 10 -11 классов, как для изучения новой темы, так и для повторения, при подготовке к ВНО,ЕГЭ,ГИА.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Решение тригонометрических уравнений и неравенств
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение тригонометрических уравнений и неравенств»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1430 руб.
2380 руб.
1800 руб.
3000 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства






![Выбери верный ответ 1. Найдите сумму корней уравнения 2 sin x + 1 = 0, принадлежащих отрезку [ 0;2 π ]](https://fsd.kopilkaurokov.ru/uploads/user_file_56e573e0a28cf/img_user_file_56e573e0a28cf_8.jpg)
![Выбери верный ответ 2. Найдите все решения уравнения tg x – ctg ( π /2 + x) + 2 = 0, принадлежащие отрезку [ 0; 2 π ]](https://fsd.kopilkaurokov.ru/uploads/user_file_56e573e0a28cf/img_user_file_56e573e0a28cf_9.jpg)

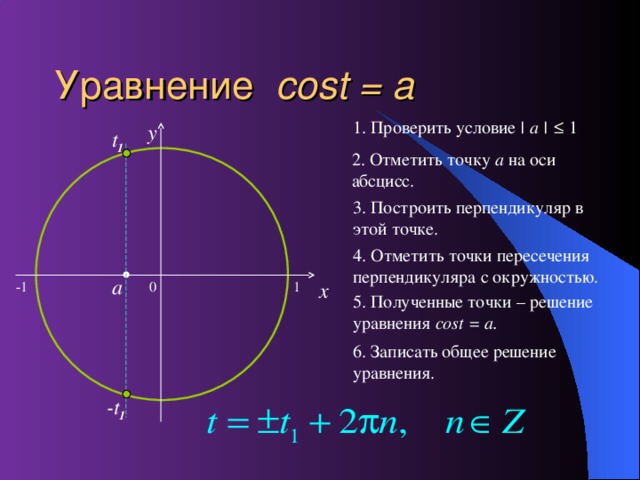
 a, cost ≤ a sint a, sint ≤ a" width="640"
a, cost ≤ a sint a, sint ≤ a" width="640"
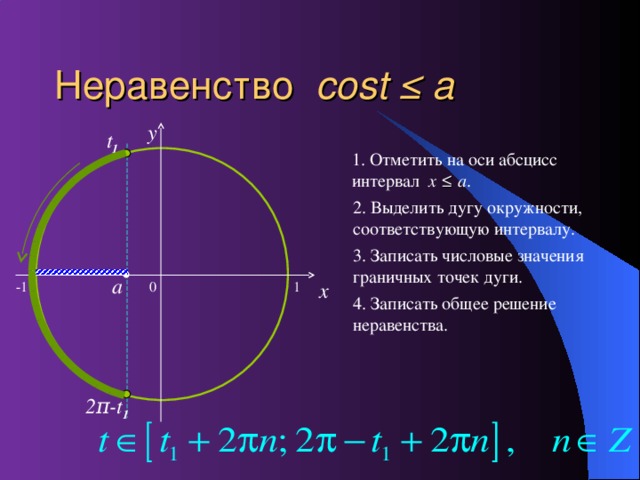
 a y t 1 1 . Отметить на оси абсцисс интервал x a . 2 . Выделить дугу окружности, соответствующую интервалу . 3. Записать числовые значения граничных точек дуги . a x 0 -1 1 4. Записать общее решение неравенства . -t 1 13" width="640"
a y t 1 1 . Отметить на оси абсцисс интервал x a . 2 . Выделить дугу окружности, соответствующую интервалу . 3. Записать числовые значения граничных точек дуги . a x 0 -1 1 4. Записать общее решение неравенства . -t 1 13" width="640"
 a y 1 1 . Отметить на оси ординат интервал y a . 2 . Выделить дугу окружности, соответствующую интервалу . t 1 π -t 1 a 3. Записать числовые значения граничных точек дуги . x 0 4. Записать общее решение неравенства . -1 15" width="640"
a y 1 1 . Отметить на оси ординат интервал y a . 2 . Выделить дугу окружности, соответствующую интервалу . t 1 π -t 1 a 3. Записать числовые значения граничных точек дуги . x 0 4. Записать общее решение неравенства . -1 15" width="640"


 a, cost ≤ a sint a, sint ≤ a Уравнения cost = a sint = a Система неравенств Решение уравнений группы ВНО" width="640"
a, cost ≤ a sint a, sint ≤ a Уравнения cost = a sint = a Система неравенств Решение уравнений группы ВНО" width="640"
















