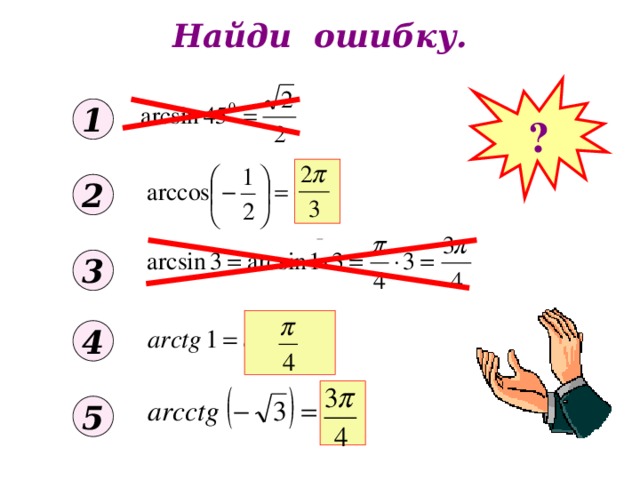
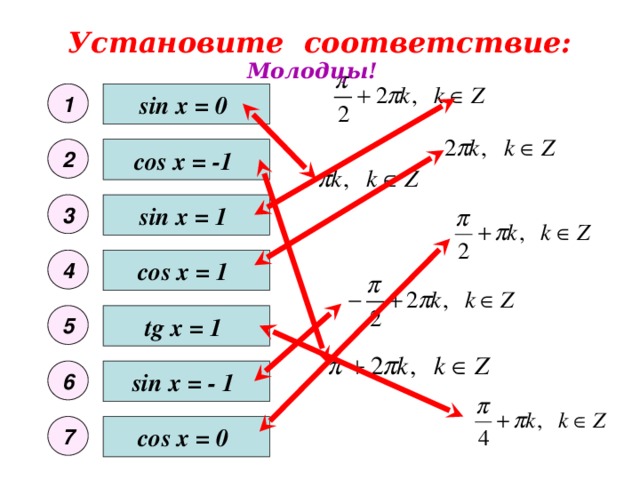
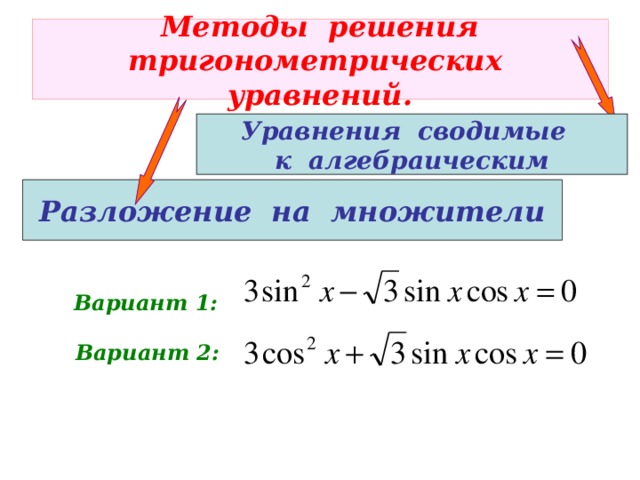
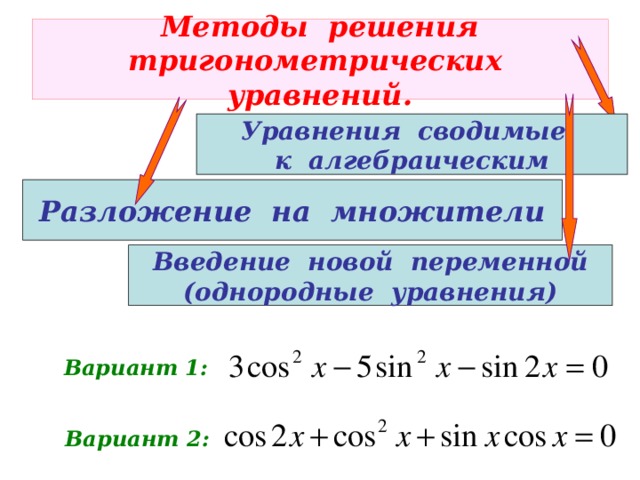
Цели урока: ввести понятия простейших тригонометрических уравнений, формул их корней; закрепить умение находить значения обратных тригонометрических функций.
- Развивающая: формировать умение анализировать, искать аналоги и различные варианты решения.
- Воспитательная: воспитывать внимательность, уверенность; активность, наблюдательность; стремление в взаимовыручке, умение работать в группе и самостоятельно.
Форма проведения: работа в группах, индивидуальная, самостоятельная.
Формы контроля: текущий.
Оборудование: презентация «Простейшие тригонометрические уравнения», проектор, экран; доска, цветной мел; листы отчета работы в группах; карточки-тесты, индивидуальные задания на карточках; листы.
В результате изучения новой темы учащиеся должны:
- знать: понятия простейших тригонометрических уравнений и формулы их корней; частные случаи простейших тригонометрических уравнений;
- уметь: применять формулы корней уравнений при решении упражнений; находить значения обратных тригонометрических функций на единичной окружности.
План проведения занятия:
1.Организационный момент
2.Проверка знаний, воспроизведение и коррекция опорных знаний.
3.Мотивационный момент
4.Изучение нового материала
5.Первичное применение приобретенных знаний: Работа в группах
6.Проверочная работа по карточкам
7.Итог занятия. Задание на дом. Рефлексия.
Вопросы по теме:
1.Какое уравнение называется тригонометрическим?
2.Что называется корнем уравнения?
3.Что является корнем тригонометрического уравнения?
4.Сколько корней может иметь тригонометрическое уравнение?
Таблица: Решение простейших тригонометрических уравнений
Формулы для повторения: ?
Частные случаи решения тригонометрических уравнений:
,,
Структура урока:
1. Организационный момент
Приветствие, проверка готовности учащихся к уроку.
2. Проверка знаний, воспроизведение и коррекция опорных знаний.
Тест с выбором ответа по 2 вариантам на карточках.
3. Мотивационный момент
– обоснование необходимости изучения данной темы, сообщение темы
– вовлечение учащихся в процесс постановки целей и задач занятия
4. Изучение нового материала
Работа с презентацией
Повторение: Определение простейшие тригонометрические уравнения – уравнения вида Sinx = a, Cosx = a, tgx = a, ctgx = a.
Работа по таблице частных случаев решения тригонометрических уравнений
1.Работа фронтально по вопросам
2.Основной принцип решения тригонометрического уравнения переход от сложного к простому, с использованием преобразований, используя формулы.
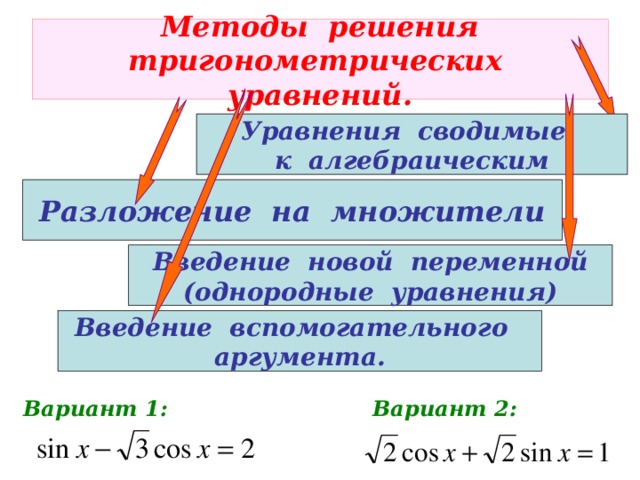
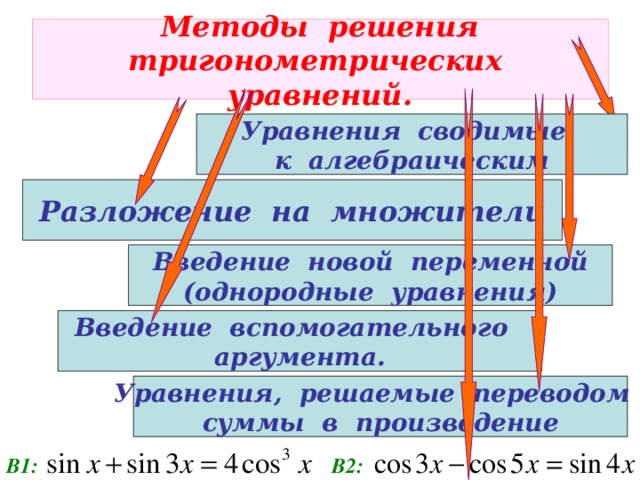
Способы решения:
1.Введение новой переменной
2.Приведение к квадратному уравнению
3.Разложение на множители
4.Однородные уравнения
5. Первичное применение приобретенных знаний: Работа в группах
Класс делится на группы по 4 человека в каждой. Каждому в группе дана карточка(4 человека-4 способа) с заданием разобрать готовое решение уравнения, по этому способу решает подобное уравнение, третий пример объясняет товарищам в группе.
1 способ: Введение новой переменной
Пример1:
Разбери и запомни способ решения примера. Обрати внимание на запись решения и ответа
Пусть, тогда заменим и получим уравнение 2а2+5а+2=0, решим его и получим что а1= –2, а2=–0,5. Вернемся к замене:
а1= –2, то, нет решений т.к. Е()=[–1;1]
а2=–0,5, то, тогда
Пример2
3 способ: Разложение на множители
Пример1:
Разбери и запомни способ решения примера. Обрати внимание на запись решения и ответа
или
Пример2:
Реши в тетради самостоятельно, применив сначала формулу, а затем вынеси общий множитель за скобки. Проверь свое решение по проверочному листу, если верно объясни решение примера 1 и примера 2 товарищам в группе.
Пример3:
Реши это уравнение вместе с товарищем по группе, выполни взаимопроверку, Сделайте выводы о виде и уравнения и способе его решения.
Аналогично способы 2 и 4.
2 способ: Приведение к квадратному уравнению.
Пример1:
Пример2:
Пример 3: 2cos2х-3
4 способ: Однородные уравнения
Работа с презентацией - определение, алгоритм решения однородных уравнений. Работа с примером по учебнику
Пример 1: Sin2x-4SinxCosx+3Cos2x=0
Пример2:
Пример 3: 2Sin2x+5SinxCosx+Cos2x=4
6.Проверочная работа по карточкам
Цель: Провести текущий контроль за усвоением решения тригонометрических у равнений, определив тип уравнения и выбрав метод решения.
1 Вариант.
1. Найти наименьший положительный корень уравнения
Ответы:
2. Запишите сумму корней уравнения принадлежащих промежутку
Ответы:
2 Вариант.
1. Решить уравнение.Найдите его наименьший положительный корень.
Ответы:
2. Решите уравнение Найдите сумму корней принадлежащих промежутку
Ответы:
Проверка самостоятельной работы индивидуальна.
Дополнительное задание. Решить систему.
и найти сумму ее решений, принадлежащих промежутку
Ответы:
Проблема: Как решить уравнение
7.Итог урока. Рефлексия.
Домашнее задание:
Цель: Закрепить навыки решения тригонометрических уравнений, выбрав для решения любые два уравнения, записать их на доке. Подготовиться к следующему уроку, выполним самостоятельную работу на 2 варианта, где нужно повторить этапы решения тригонометрических неравенств.
№166(б,г), 170(а,в), 171(а,в)