"Рациональная дробь. Сокращение дробей"

Открытый урок алгебры в 7 классе

Тема: «Рациональная дробь и ее основное свойство. Сокращение рациональных дробей.»

10/16/16

Выполнила: учитель математики

ГУ «Сары-Обинская с.ш.» Осипова Н.Н .

2015-2016 уч. г.

.

Теоретический опрос учащихся

1. Какие дроби называются рациональными дробями?

Приведите пример рациональной дроби.

2. Какие выражения называются тождественно

равными выражениями?

3. Что называется тождественным преобразованием?

4.Сформулировать основное свойство рациональной

дроби

5. Сформулировать следствия, вытекающие из

основного свойства рациональной дроби.

ОСНОВНОЕ СВОЙСТВО РАЦИОНАЛЬНОЙ ДРОБИ ДРОБИ.

где В≠0 и N ≠0

Величина рациональной дроби не изменится, если числитель и знаменатель дроби умножить

( или разделить) на одно и то же выражение, не равное нулю.

д в а т и п а з а д а н и й, при выполнении которых применяется основное свойство дроби :

– приведение дробей к новому знаменателю;

– сокращение дробей.

Следствия, вытекающие из основного свойства рациональной дроби

Математический диктант

Формулы сокращенного умножения:

• квадрат суммы двух выражений;
• квадрат разности двух выражений;
• разность квадратов двух выражений;
• сумма кубов двух выражений;
• разность кубов двух выражений;
• куб суммы двух выражений;
• куб разности двух выражений.

Задания на приведение дробей к новому знаменателю (устно)

1. Умножьте числитель и знаменатель дроби на указанное число.

а) на 5; б) на 2; в) на 6.

Упражнения

3. Заполните пустые места так, чтобы равенство было верным:

• ; 2) ; 3) ;

4) ; 5) ; 6) .

Упражнения

№ 240(1,4) прорешать на доске и в тетрадях

Сокращение дробей

Устно

– Сократите обыкновенные дроби:

а) ; б) ; в) ; г) ;

д) ; е) ; ж) ; з) .

Задания на сокращение рациональных дробей (устно)

Разделите числитель и знаменатель рациональной

дроби на указанное число:

а) на 2; б) на 3; в) на 5.

Способы разложения многочлена на множители:

• Вынесение общего множителя за скобки:

2) Способ группировки:

=

3) Применение формул сокращенного умножения:

=(=

=

З а д а н и я и в о п р о с ы :

Разложите на множители многочлен:

а) х 2 у – 2 х ; д) х 2 + 6 х + 9;

б) 3 a 2 b – 9 ab 2 ; е) а 2 – 10 а + 25;

в) т 2 – 4 m ; ж) ax + bx + ay + by .

г) а 3 – а ; з) ab – b + 3 a – 3.

Задания на сокращение рациональных дробей ( письменно) прорешать на доске и в тетрадях

№ 239(1,4,5)

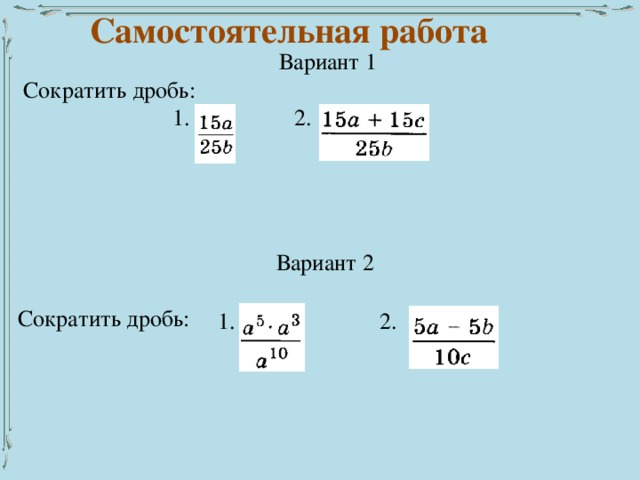
Самостоятельная работа

Вариант 1

Сократить дробь:

1. 2.

Вариант 2

Сократить дробь:

1. 2.

Домашнее задание :

§ 12, № , № 239 (2)

№ 240 (2), № 243 (2)

В о п р о с ы рефлексии:

– В чём состоит основное свойство рациональной дроби?

– Что такое тождество?

– Когда применяется основное свойство дроби?