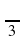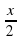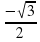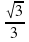Урок алгебры и начала анализа в 10 классе
учитель математики СОШ №48 Пономаренко И.И.
ТЕМА: Простейшие тригонометрические уравнения
ТИП УРОКА: урок применения знаний и умений
ЦЕЛИ: а) закрепить и проверить навыки решения
простейших тригонометрических уравнений;
б) развитие математического мышления;
в) воспитание усердия и упорства, желание добиться успеха
ФОРМЫ И МЕТОДЫ: фронтальные, индивидуальные, ИКТ
ОБОРУДОВАНИЕ: компьютер, компьютерный проектор, экран, листы ответов,
тесты
КОМПЬЮТЕРНАЯ ПРЕЗЕНТАЦИЯ: приложение
Просмотр содержимого документа
«ЛИСТ ОТВЕТОВ»
Просмотр содержимого документа
«Урок алгебры и начала анализа в 10 классе»
Урок алгебры и начала анализа в 10 классе
учитель математики СОШ №48 Пономаренко И.И.
ТЕМА: Простейшие тригонометрические уравнения
ТИП УРОКА: урок применения знаний и умений
ЦЕЛИ: а) закрепить и проверить навыки решения
простейших тригонометрических уравнений;
б) развитие математического мышления;
в) воспитание усердия и упорства, желание добиться успеха
ФОРМЫ И МЕТОДЫ: фронтальные, индивидуальные, ИКТ
ОБОРУДОВАНИЕ: компьютер, компьютерный проектор, экран, листы ответов,
тесты
КОМПЬЮТЕРНАЯ ПРЕЗЕНТАЦИЯ: приложение
ХОД УРОКА:
1 Организационный момент
2. Актуализация знаний.
Сегодня мы завершаем работу по теме «Простейшие тригонометрические уравнения». Целью нашего урока будет еще раз повторить необходимый материал для успешного решения простейших тригонометрических уравнений и возможность каждому из вас самому оценить степень усвоения материала по изученной теме.
Эпиграфом нашего урока послужат слова А.Нивена « Математику нельзя изучать, наблюдая, как это делает сосед» (слайд 1)
И начнем урок с подготовительной части «Теоретической»
Заполнить пропуски указав, закономерность составления строк (слайд 2)
Для каждой, изученной нами тригонометрической функции существует
обратная тригонометрическая функция. Указать их и дать им определение.
Вычислить значение: arccos 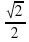 и т.д. (слайд 3)
и т.д. (слайд 3)
Какие уравнения мы называем простейшими тригонометрическими?
При каких значения а уравнения sinx = a и cosx = a имеют корни, а при каких нет?
3 Решение задач
Установить соответствие между простейшим тригонометрическим уравнением и его решением (слайд 4) – взаимопроверка
Указать решения частных случаев простейших тригонометрических уравнений (слайд 5) – самопроверка (в кружках поставить «+» или « -» в зависимости от вашего ответа)
Переходим к «Практической» части урока
Тест « Пятиминутка» - заполнить таблицу, указав букву , соответствующую правильному решению уравнения (слайд 6) - самопроверка
(в кружках поставить «+» или « -» в зависимости от вашего ответа)
Указав алгоритм решения уравнений, решить их (работа в тетрадях)
а) 2cosx = 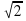
б) 2 sin (- 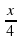 ) =
) = 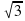 - двое учащихся работают самостоятельно на откидных досках, остальные в тетрадях
- двое учащихся работают самостоятельно на откидных досках, остальные в тетрадях
в) cos (7x - 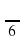 ) = -1 - учащийся решает у доски с объяснением
) = -1 - учащийся решает у доски с объяснением
Итак, мы подошли к последнему этапу нашего урока проверочной работе «Я сумею, я смогу…». Каждый может выбрать тот уровень сложности уравнений, который ему под силу, но каждому уровню соответствует своя оценка:
(слайд 7) 1 вариант:
«3» «4» «5»
| 2 cos x = 1 | | sin x = -2 | | 3 tg x = 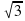 | | 2 cos x= -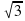 | | 4 ctg x + 4 =0 | sin 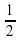 x = 1 x = 1 | 2cos (4x - 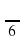 ) = ) = 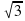 |
| 2 cos 0,5x = 1 | 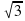 tg(3x + tg(3x + 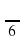 ) = 1 ) = 1
|
| cos 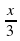 = - = - 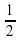 | sin(2x - 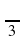 ) = - 0,5 ) = - 0,5 |
| ctg 4x = 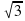 |
2 вариант:
«3» «4» «5»
| 2 sin x = - 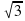 | | 3 tg x = 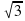 | | 2 cos x =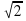 | | 2tg x =0 | | cos x = -5 | cos 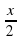 = 1 = 1 | 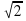 cos (2x- cos (2x- 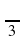 ) = 1 ) = 1
|
| sin 4x = 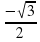 | 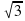 tg(2x - tg(2x - 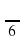 ) = 3 ) = 3
|
| 2sin 0,5x = 1 | sin(2x - 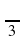 ) = - 0,5 ) = - 0,5 |
| tg(- 2x) = - 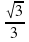 |
И закончить урок хочется словами великого педагога Я.А.Каменского:
«Считай несчастным тот день или час, в который ты не усвоил ничего нового, и ничего нового не прибавил к своему образованию» (слайд 8)
4.Задание на дом: Т.2013: в4(6), в7(5), в11(7),в 12(7),в14(14)
Просмотр содержимого презентации
«Презентация 10кл»

учитель математики СОШ №48 Пономаренко И.И.
Простейшие тригонометрические уравнения
Математику нельзя изучать, наблюдая, как это делает сосед!
А. Нивен

Цель урока: применение знаний по теме на практике
Задачи:
- образовательные: научить применять полученные знания на практике; оперировать имеющимся потенциалом в конкретной ситуации;
- развивающие: развить математическое мышление, совершенствовать навыки анализа, обобщения;
- воспитательные: вовлечь в активную деятельность,
воспитание усердия и упорства, желания добиться успеха
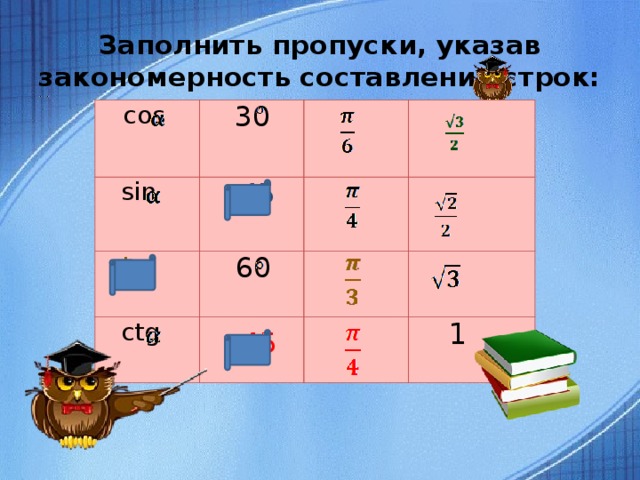
Заполнить пропуски, указав закономерность составления строк:
cos
30
sin
45
tg
ctg
60
45
1

Вычислить:
arccos
arcsin
arctg
-
arccos
arcctg
arccos
arctg 1
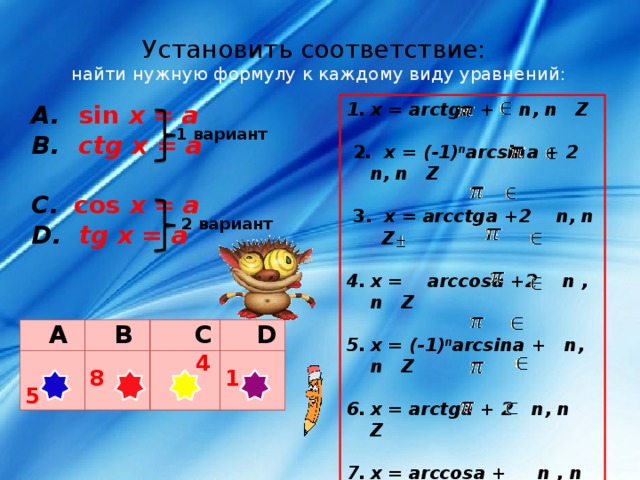
Установить соответствие: найти нужную формулу к каждому виду уравнений:
2 . x = (-1) n arcsina + 2 n, n Z
3. x = arcctga +2 n, n Z
- x = (-1) n arcsina + n, n Z
А. sin х = а
В. ctg х = а
С. сos х = а
D. tg х = а
1 вариант
2 вариант
А
В
5
С
8
D
4
1
n, n
Z 7. x = arccosa +
, n
Z
4. x =
arccosa +
, n
Z 8. x = arcctga +
n, n
Z

Частные случаи решения простейших тригонометрических уравнений
1 вариант 2 вариант
cos x = 0 sin x = 0
cos x = 1 sin x = 1
cos x = -1 sin x = -1
x = + n, n Z x= n, n Z
x = 2 n, n Z x= +2 n, n Z
x = + 2 n , n Z x = - +2 n, n Z
tg x = 1
x = + n,
tgx = - 1
tgx = 0
x = - + n,
x = n,
n Z
ctgx = 1
n Z
x = + n,
n Z
ctgx = -1
x = + n,
ctgx = 0
n Z
x = + n,
n Z
n Z
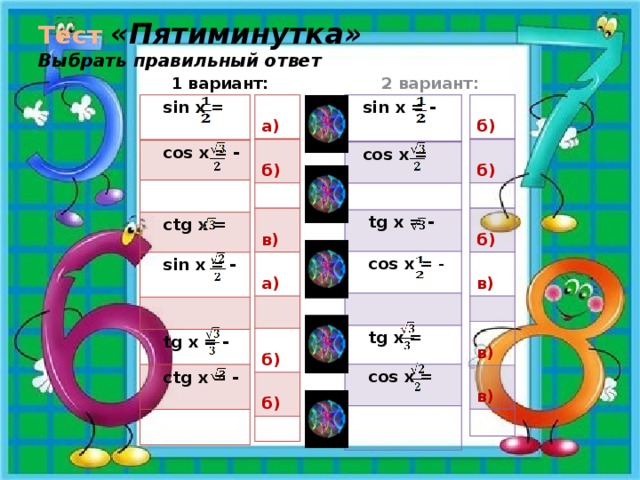
Тест «Пятиминутка» Выбрать правильный ответ
2 вариант:
1 вариант:
а)
sin x =
sin x = -
б)
б)
cos x =
cos x = -
б)
tg x = -
б)
ctg x =
в)
sin x = -
а)
cos x = -
в)
б)
tg x =
tg x = -
в)
ctg x = -
в)
cоs x =
б)

Проверочная работа «Я сумею, я смогу …»
1 вариант
2 вариант
2 sin x =-
2 cos x = 1
sin x = -2
3 tg x =
2 cos x =
3 tg x =
2 cos x= -
2tg x = 0
4 ctg x + 4 =0
cos x = -5
cos = 1
sin 4x =
2sin 0,5x = 1
tg(- 2x) = -
sin x = 1
2 cos 0,5x = 1
cos = -
ctg 4x =
cos (2x- ) = 1
2cos (4x - ) =
tg(2x - ) = 3
tg(3x + ) = 1
sin(2x - ) = - 0,5
sin(2x - ) = - 0,5

Считай несчастным тот день или час, в который ты не усвоил ничего нового, и ничего не прибавил к своему образованию Я. А. Каменский
Домашнее задание:
Т 2013: в4 (6), в7 (5),
в11 (7), в 12 (7), в14 (14)

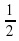

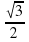
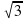
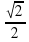
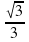

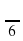
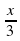 = -
= - 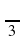

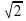
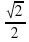 и т.д. (слайд 3)
и т.д. (слайд 3)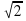
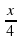 ) =
) = 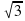 - двое учащихся работают самостоятельно на откидных досках, остальные в тетрадях
- двое учащихся работают самостоятельно на откидных досках, остальные в тетрадях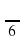 ) = -1 - учащийся решает у доски с объяснением
) = -1 - учащийся решает у доски с объяснением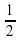
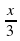 = -
= -