Производная в задачах ЕГЭ

Данную презентацию можно использовать на элективных курсах и при подготовке к ЕГЭ

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Производная в задачах ЕГЭ»

Тема урока:

«Производная в задачах ЕГЭ»

Подумай

Зачем нужна производная?

2. Где мы встречаемся с производной и используем её?

3. Можно ли без неё обойтись в математике и не только?

Вывод:

Производная - одно из самых важных понятий математического анализа. Знание производной необходимо инженерам-технологам, конструкторам, экономистам, физикам, учёным.

Устный счёт. Ответьте на вопросы

Что такое производная?
В чём заключается механический (физический) и геометрический смыслы производной?
Что такое точки экстремума функции?
Сформулируйте необходимое условие экстремума.
Сформулируйте достаточные условия экстремума?
Что такое стационарные точки?
Сформулируйте достаточные условия монотонности функции?
Как найти промежутки монотонности функции по графику производной?
Каковы этапы нахождения экстремумов функции?
Как найти наибольшее и наименьшее значение функции на отрезке?

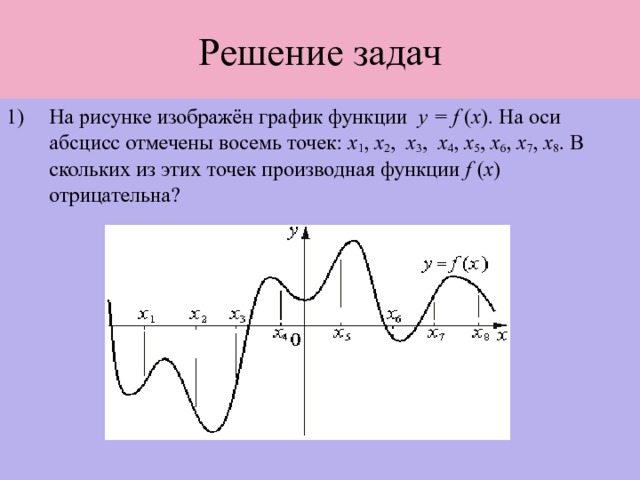
Решение задач

На рисунке изображён график функции y = f ( x ). На оси абсцисс отмечены восемь точек: х 1 , х 2 , х 3 , х 4 , х 5 , х 6 , х 7 , х 8 . В скольких из этих точек производная функции f ( x ) отрицательна?

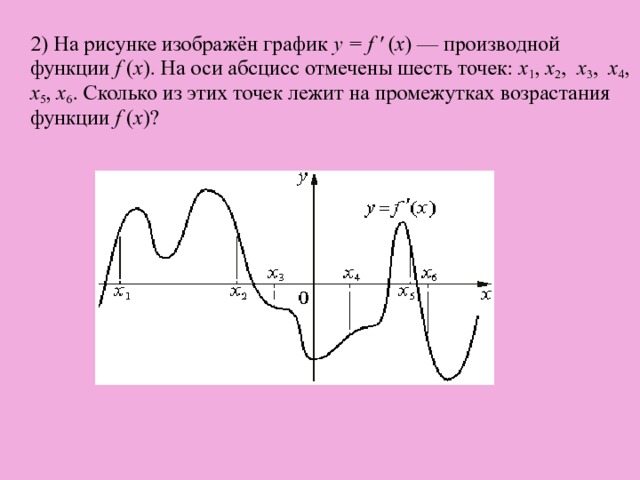
2) На рисунке изображён график y = f ' ( x ) — производной функции f ( x ). На оси абсцисс отмечены шесть точек: х 1 , х 2 , х 3 , х 4 , х 5 , х 6 . Сколько из этих точек лежит на промежутках возрастания функции f ( x )?

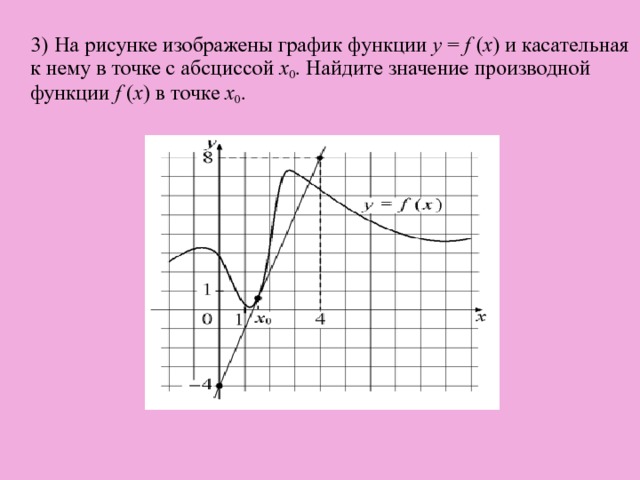
3) На рисунке изображены график функции y = f ( x ) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f ( x ) в точке x 0 .

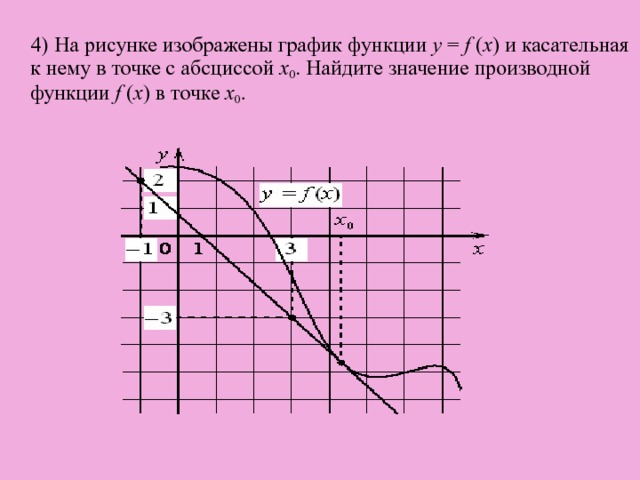
4) На рисунке изображены график функции y = f ( x ) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f ( x ) в точке x 0 .

5) На рисунке изображён график y = f ′ ( x ) — производной функции f ( x ), определённой на интервале (−9; 8). Найдите точку экстремума функции f ( x ) на отрезке [−3; 3].

6) На рисунке изображён график функции y = f ( x ), определённой на интервале (− 9; 5). Найдите количество точек, в которых производная функции f ( x ) равна 0.

7) Материальная точка движется прямолинейно по закону x ( t ) = t 2 + 4 t + 27, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t = 2 с.

Групповая работа

Задания для 1 группы
1) Найдите наибольшее значение функции y = x 3 − 6 x 2 + 9 x + 5 на отрезке [0;3].
2)Найдите наибольшее значение функции y =
Задания для 2 группы
1) Найдите наименьшее значение функции
y = e 2 x − 4e x + 4 на отрезке [− 1; 2].
2) Найдите наименьшее значение функции y =

Тестирование

http://www.ege-online-test.ru/

Подведение итогов

Я почувствовал…
Я научился…
У меня получилось …
Я смог…
Я попробую …
Меня удивило, что …
Мне захотелось…

«Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника».

Фома Аквинский

Желаю успехов в подготовке к ЕГЭ!

Домашнее задание

повторить теоретический материал по теме «Производная функции»;

2) на сайте «Открытый банк заданий по математике» ( http://mathege.ru/ ) найти прототипы заданий №7 и №12 и решить не менее 10 задач.

Предмет: Математика

Категория: Презентации

Целевая аудитория: 11 класс.
Урок соответствует ФГОС

Скачать
Производная в задачах ЕГЭ

Автор: Кузнецова Марина Сергеевна

Дата: 23.09.2016

Номер свидетельства: 345495

Похожие файлы

Факультативное занятие "Производная функция в заданиях ЕГЭ"

object(ArrayObject)#864 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(110) "Факультативное занятие "Производная функция в заданиях ЕГЭ""
    ["seo_title"] => string(62) "fakultativnoe_zaniatie_proizvodnaia_funktsiia_v_zadaniiakh_ege"
    ["file_id"] => string(6) "487932"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1543343615"
  }
}

Конспект открытого урока по математике 10 класса "Применение производной для исследования функций на монотонность и экстремумы"

object(ArrayObject)#886 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(236) "Конспект открытого урока по математике 10 класса "Применение производной для исследования функций на монотонность и экстремумы" "
    ["seo_title"] => string(136) "konspiekt-otkrytogho-uroka-po-matiematikie-10-klassa-primienieniie-proizvodnoi-dlia-issliedovaniia-funktsii-na-monotonnost-i-ekstriemumy"
    ["file_id"] => string(6) "124820"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1414790423"
  }
}

Урок по теме:"Геометрический смысл производной. Уравнение касательной."

object(ArrayObject)#864 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(132) "Урок по теме:"Геометрический смысл производной. Уравнение касательной." "
    ["seo_title"] => string(76) "urok-po-tiemie-gieomietrichieskii-smysl-proizvodnoi-uravnieniie-kasatiel-noi"
    ["file_id"] => string(6) "103881"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1402644901"
  }
}

Урок "Вычисление производных элементарных функций"

object(ArrayObject)#886 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(95) "Урок "Вычисление производных элементарных функций" "
    ["seo_title"] => string(56) "urok-vychislieniie-proizvodnykh-eliemientarnykh-funktsii"
    ["file_id"] => string(6) "148062"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1419572457"
  }
}

Производная. Применение производной для исследования функций. Подготовка к ЕГЭ.

object(ArrayObject)#864 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(148) "Производная. Применение производной для исследования функций. Подготовка к ЕГЭ. "
    ["seo_title"] => string(86) "proizvodnaia-primienieniie-proizvodnoi-dlia-issliedovaniia-funktsii-podghotovka-k-iege"
    ["file_id"] => string(6) "124824"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1414791207"
  }
}

Производная в задачах ЕГЭ

Просмотр содержимого документа «Производная в задачах ЕГЭ»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Производная в задачах ЕГЭ»