Применение пароизводной к исследованию функций.История возникновения производной. Разминка с нахождением производных.Признак возрастания и убывания функций. Задачи по готовым ченртежам, Критические точки. Достаточное условие экстремума функции, исследование функции с помощью производной и построение графикафункций. Схема исследования функций, эскиз графика функций, образец выполнения работы. Задачи на нахождение наибольшего и наименьшего значения функций, правило нахождения наибольшего и наименьшего значения функции на отрезке.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
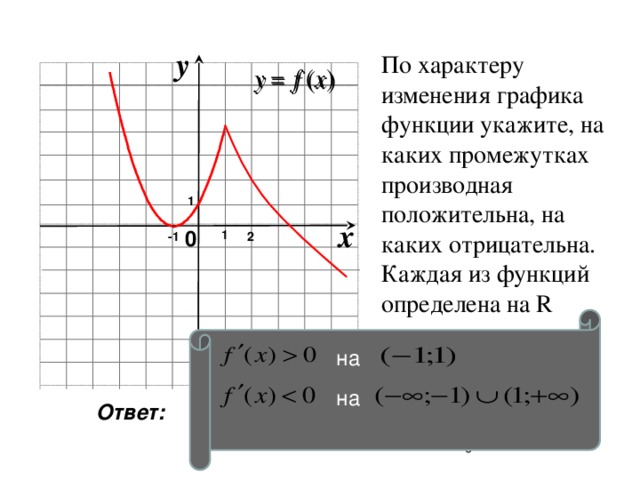
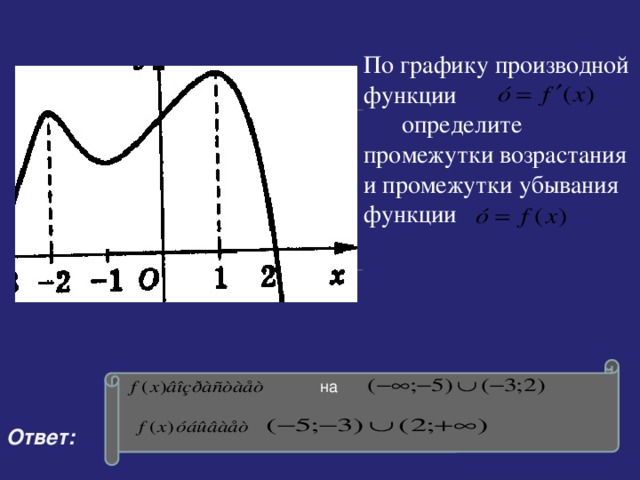
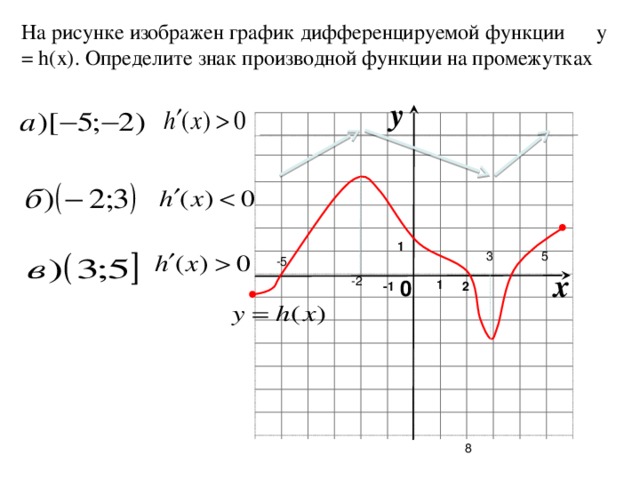
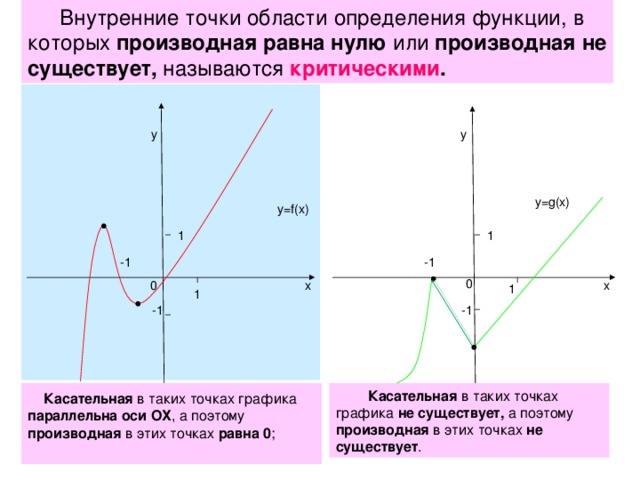
Применение производной - 10 класс
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
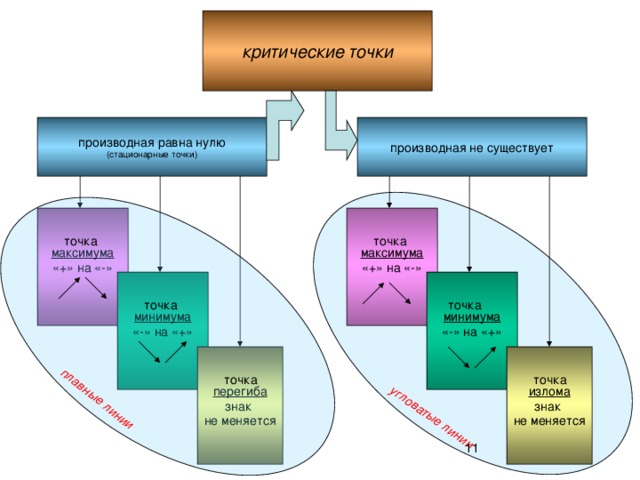
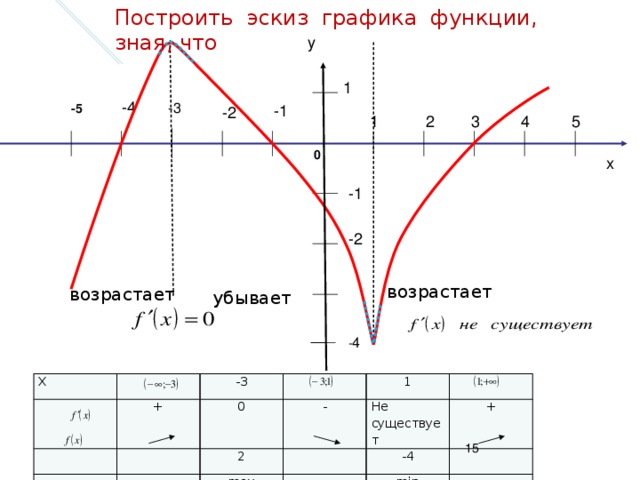
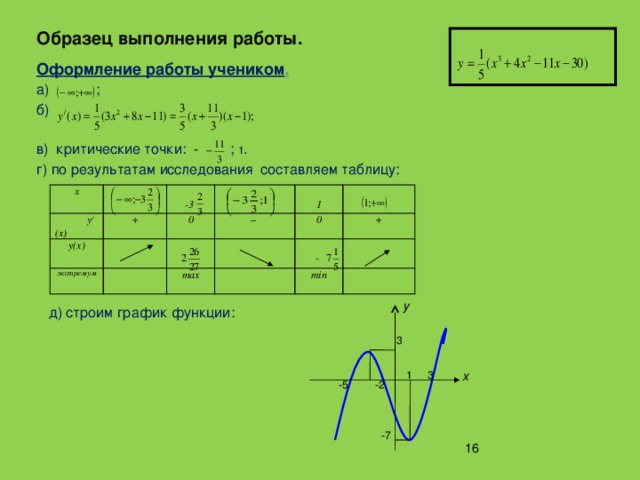
«применение производной - 10 класс »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1730 руб.
2880 руб.
1910 руб.
3190 руб.
1400 руб.
2330 руб.
1800 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства










![Правило нахождения наибольшего и наименьшего значений функции f(x) на отрезке [a;b] Чтобы найти наибольшее и наименьшее значения непрерывной функции f(x) на промежутке [a;b], нужно вычислить её значения f(a) и f(b) на концах данного промежутка вычислить её значения в критических точках, принадлежащих этому промежутку выбрать из них наибольшее и наименьшее. Записывают так: max f(x) и min f(x) [a;b] [a;b]](https://fsd.kopilkaurokov.ru/uploads/user_file_546e09956de3f/img_user_file_546e09956de3f_17.jpg)
















