Презентация "Задачи на координатной плоскости"

Презентация у уроку : Задачи на координатной плоскости.итель

Учитель: Сарнадская Надежда Анатольевна, МБОУ Гимназия №1 г. Североморск

Класс: 8

УМК: Г. В. Дорофеев, Математика,8

Эпиграф: «Математике должно учить в школе еще с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни». Н. И. Лобачевский

Цели урока:

Основная цель: формировать умения переносить знания в новую ситуацию.

Задачи:

-формировать у обучающихся умение составлять уравнения прямых по различным условиям; -познакомить с применением систем уравнений при решении задач на координатной плоскости; -закрепить геометрический смысл коэффициентов k и l в уравнении прямой у=kx+l; -обеспечить овладение алгоритмическими приемами при решении задач.

Развивающие:

-развивать логическое мышление, математическую речь, вычислительные навыки; - совершенствовать умения анализировать, сравнивать, сопоставлять; -формировать потребность приобретения новых знаний; - развивать коммуникативные универсальные умения: общаться, вести диалоги.

Воспитывающие:

-воспитание познавательного интереса к предмету. – реализация межпредметных связей с физикой, экономикой, химией, информатикой.

Тип урока: урок применения знаний и умений.

Оборудование: компьютер, экран, тетрадь, карточки для выполнения индивидуальной работы

Ход урока.

Организационный момент.

-сообщение темы урока, целей урока, структуры урока.

Повторение. Проверка Домашнего задания.

Устная работа. (Презентация)

Актуализация знаний.

На этом уроке обучающиеся не получают новых теоретических сведений. Они должны применить полученные ранее знания и умения, чтобы научиться записывать уравнения прямых, отвечающих различным условиям.

С этой целью необходимо актуализировать знания учащихся (частично это уже было сделано при проведении устной работы) и рассмотреть с ними несколько примеров, показывающих, как может быть составлено уравнение прямой.

При актуализации знаний следует затронуть такие вопросы:

- геометрический смысл коэффициентов k и l в линейном уравнении

у = kx+l;

- условие параллельности прямых;

- условие принадлежности точки с заданными координатами графику некоторого уравнения.

Для этого предложить учащимся два задания.

Обучающиеся самостоятельно выполняют эти задания, затем проверяют только первое задание с помощью информации, представленной в виде электронной презентации, отмечая правильность своих ответов в таблице. После этого работы сдаются.

Вариант 1

Дана прямая.

Правильность ответа

Какой угол (тупой или острый) образует эта прямая с положительным направлением оси абсцисс?

В какой точке прямая пересекает ось ординат?

Проходит ли эта прямая через точку с координатами (– 2; 4)?

Параллельна ли она прямой у = – 2х+3?

Задание 2:

Запишите уравнение любой прямой:

образующей тупой угол с положительным направлением оси абсцисс и пересекающей ось ординат в точке (0; – 1)

образующей острый угол с положительным направлением оси абсцисс и проходящей через точку (0;3)

проходящей через начало координат параллельно прямой

у = – 3х+5

Вариант 2

Дана прямая .

Правильность ответа

Какой угол (тупой или острый) образует эта прямая с положительным направлением оси абсцисс?

В какой точке прямая пересекает ось ординат?

Проходит ли эта прямая через точку с координатами (– 2; 4)?

Параллельна ли она прямой у = – 2х+3?

Задание 2:

Запишите уравнение любой прямой:

образующей острый угол с положительным направлением оси абсцисс и пересекающей ось ординат в точке (0; 4)

образующей тупой угол с положительным направлением оси абсцисс и проходящей через точку (0; –7 )

проходящей через начало координат параллельно прямой

у = х – 8

- Проверьте решение первого задания на экране. Если выполнено верно, поставьте плюс, если не верно – минус. (презентация)

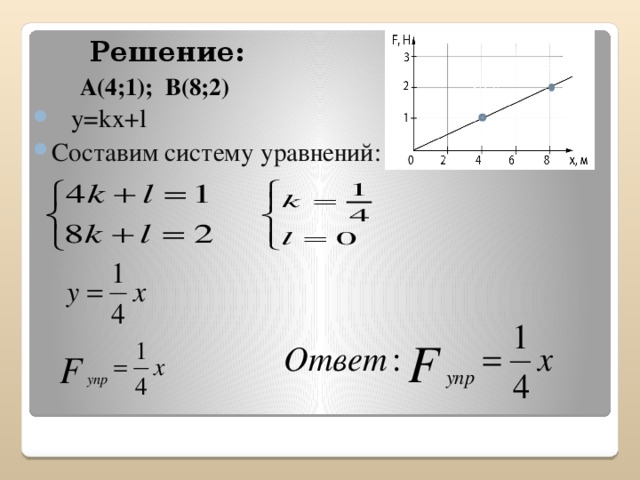
После выполнения этих заданий рассмотреть две задачи, вырабатывая алгоритм решения задач. (Презентация). Учащиеся в тетрадях записывают основное решение.

Задача 1. Записать уравнение прямой, которая параллельна прямой и проходит через точку А(4; – 1).

План решения задачи.

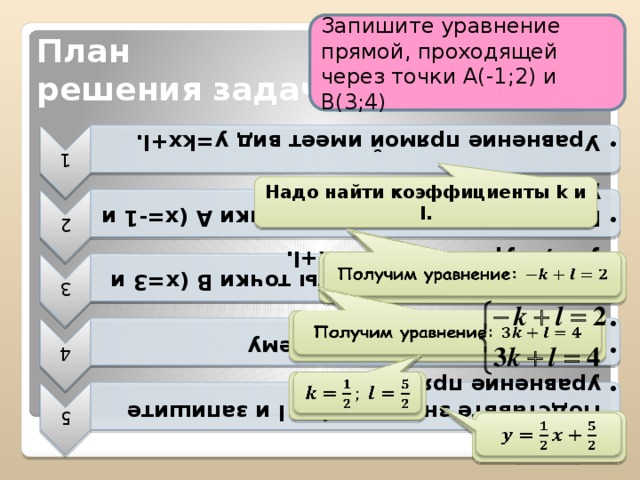
Задача 2. Записать уравнение прямой, проходящей через точки А(– 1;2) и В(3;4).

План решения задачи.

Домашнее задание: п. 4.6; № 668(б), 672(б), 673(б)
Итоги урока.

Рассмотреть применение данной темы. (Задачи из других наук, подготовленные учащимися).

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Презентация "Задачи на координатной плоскости"»

Тема урока: ЗАДАЧИ НА КООРДИНАТНОЙ ПЛОСКОСТИ

Математике д о лжно учиться в школе с той целью, чтобы познания, здесь приобретаемые, были достаточными для обыкновенных потребностей в жизни.

Н. И. Лобачевский

УСТНАЯ РАБОТА

а) параллельны;

б) проходят через начало координат;

в) образуют острый угол с положительным направлением оси абсцисс;

г) образуют тупой угол с положительным направлением оси абсцисс;

д) в какой точке каждая из этих прямых пересекает ось ординат?

Тема урока: ЗАДАЧИ НА КООРДИНАТНОЙ ПЛОСКОСТИ.

Н. И. Лобачевский.

II этап. Проверочная работа.

ЗАДАНИЕ 1

Тема урока: ЗАДАЧИ НА КООРДИНАТНОЙ ПЛОСКОСТИ.

Н. И. Лобачевский.

III этап. Решение задач на координатной плоскости.

Задача1

запишите уравнение прямой, которая параллельна прямойи проходит через точку А(4;-1) .

Запишите уравнение прямой, которая параллельна прямой

у=- ½х+3 и проходит через т. А(4;-1)

Уравнение прямой имеет вид y=kx+l.
Уравнение прямой имеет вид y=kx+l.

Примените условие параллельности прямых.
Примените условие параллельности прямых.

Определите угловой коэффициент прямой, уравнение которой должны записать.
Определите угловой коэффициент прямой, уравнение которой должны записать.

Используйте условие принадлежности точки с данными координатами графику некоторого уравнения.
Используйте условие принадлежности точки с данными координатами графику некоторого уравнения.

Подставьте x=4 и y=-1 в уравнение и найти l.
Подставьте x=4 и y=-1 в уравнение и найти l.

Запишите уравнение прямой.
Запишите уравнение прямой.

План решения задачи:

Прямые параллельны, если их угловые коэффициенты равны.

x+l

Так как точка А(4;-1) лежит на этой прямой, то ее координаты х=4 и у=-1 обращают уравнение в верное равенство.

Ответ:

Уравнение прямой, параллельной прямой и проходит через точку А(4;-1) имеет вид

Задача 2

Запишите уравнение прямой, проходящей через точки А(-1;2) и В(3;4)

1 Уравнение прямой имеет вид y=kx+l. Уравнение прямой имеет вид y=kx+l. 2 Подставьте координаты точки А (x=-1 и y=2) в уравнение y=kx+l. Подставьте координаты точки А (x=-1 и y=2) в уравнение y=kx+l. 3 Подставьте координаты точки В (x=3 и y=4) в уравнение y=kx+l. Подставьте координаты точки В (x=3 и y=4) в уравнение y=kx+l. 4 Составьте и решите систему уравнений Составьте и решите систему уравнений 5 Подставьте значения k и l и запишите уравнение прямой. Подставьте значения k и l и запишите уравнение прямой. Запишите уравнение прямой, проходящей через точки А(-1;2) и В(3;4) План решения задачи: Надо найти коэффициенты k и l. Получим уравнение: Получим уравнение:

Уравнение прямой имеет вид y=kx+l.
Уравнение прямой имеет вид y=kx+l.

Подставьте координаты точки А (x=-1 и y=2) в уравнение y=kx+l.
Подставьте координаты точки А (x=-1 и y=2) в уравнение y=kx+l.

Подставьте координаты точки В (x=3 и y=4) в уравнение y=kx+l.
Подставьте координаты точки В (x=3 и y=4) в уравнение y=kx+l.

Составьте и решите систему уравнений
Составьте и решите систему
уравнений

Подставьте значения k и l и запишите уравнение прямой.
Подставьте значения k и l и запишите
уравнение прямой.

Запишите уравнение прямой, проходящей через точки А(-1;2) и В(3;4)

План решения задачи:

Надо найти коэффициенты k и l.

Получим уравнение:

Ответ:

Домашнее задание:

п. 4.6, № 668(б), № 672(б),

№ 673(б)

Тема урока: ЗАДАЧИ НА КООРДИНАТНОЙ ПЛОСКОСТИ.

Н. И. Лобачевский.

IV этап. Применение математических знаний при изучении других наук.

Задача по экономике

Известно, что предприятие производит ноутбуки. Затраты на производство составляют с тыс.рублей при выпуске а штук продукции в месяц. Если предприятие будет производить b штук этой же продукции в месяц, то затраты составят d тыс.рублей. Вычислите затраты предприятия, если оно будет выпускать р ноутбуков в месяц, а формула затрат имеет вид R(x)=αx+β.

Варианты: 1. a=10 ,b=8 ,c=150 ,d=128 ,p=11. 2. a=260 ,b=200 ,c=5250 ,d=4050 ,p=210. 3. a=190 ,b=210 ,c=1350 ,d=1450 ,p=240. 4. a=80 ,b=100 ,c=1160 ,d=1350 ,p=105.

Решение задачи варианта 1 ( a =10 , b =8 ,c =150 , d =128 ,p=11). R(x)=αx+β.

Составим и решим систему уравнений:

α=11, β=400
R(x)=11x+400
p=11
R(11)=11∙11+400= 521

Ответ:

521 тыс.рублей – затраты на производство 11 ноутбуков.

Тема урока: ЗАДАЧИ НА КООРДИНАТНОЙ ПЛОСКОСТИ.

Н. И. Лобачевский.

IV этап. Применение математических знаний при изучении других наук.

Задача по информатике

(алгоритмика)

Условие задачи

Исполнитель Кузнечик живет на числовой оси. Кузнечик может выполнять следующие команды:

Вперед n (Кузнечик прыгает вперед на n единиц),

Назад m (Кузнечик прыгает назад на m единиц),

где переменные n и m – целые положительные числа.

Известно, что Кузнечик начал путь из точки А и выполнил программу из 40 команд, среди которых команд «Назад3» оказалось на 4 больше, чем команд «Вперед5». Какую одну команду необходимо выполнить Кузнечику, чтобы вернуться в точку А ?