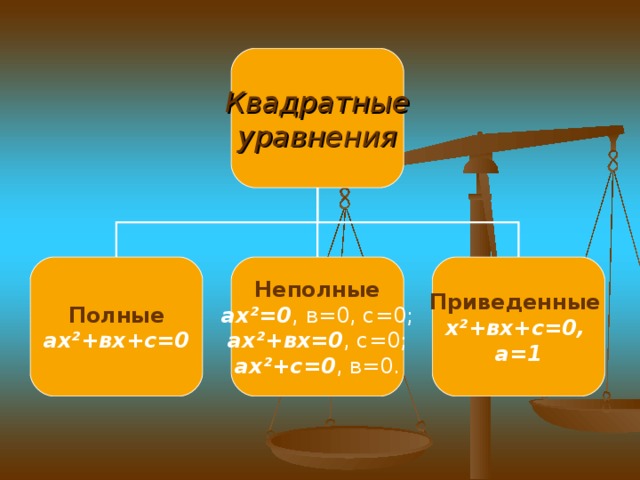
Данная презентация может быть использована как на уроке алгебры, так и на представлении проекта на ученических конференциях.
основные приемы теоремы Виета:
1. Вычисление суммы и произведения корней квадратного уравнения, не находя при этом сами корни;
2. Составление квадратных уравнений по их корням;
3. Подбор корней квадратного уравнения;
4. Исследование знаков корней квадратного уравнения;
5. Проверка правильности решения квадратного уравнения.