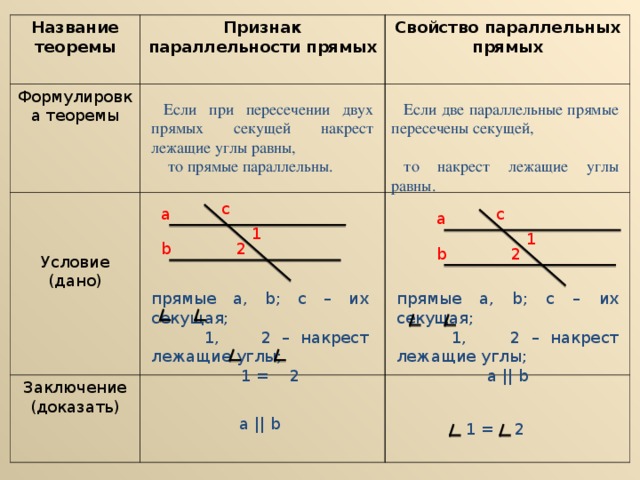
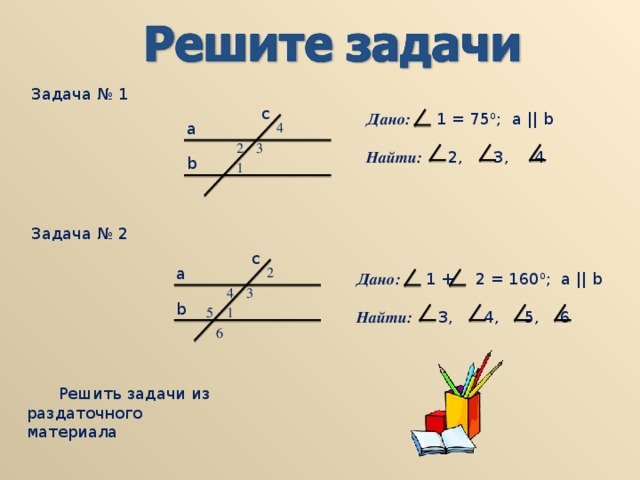
УРОК ГЕОМЕТРИИ В 7 КЛАССЕ ПО ТЕМЕ: «СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ».
ЦЕЛЬ УРОКА:
ЗАДАЧИ УРОКА:
•научить учащихся применять свойства параллельных прямых; закрепить знания, умения, навыки учащихся по теме «Аксиома параллельных прямых».
•развивать умение сравнивать, анализировать, обобщать, делать вывод, осуществлять перенос знаний и умений в новой нестандартной ситуации;
•воспитывать сознательное отношение к труду, расширять кругозор учащихся.
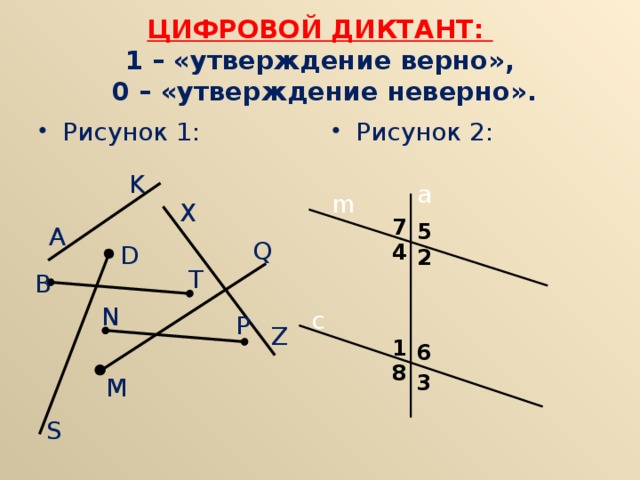
ЦИФРОВОЙ ДИКТАНТ:
1 – «утверждение верно»,
0 – «утверждение неверно».
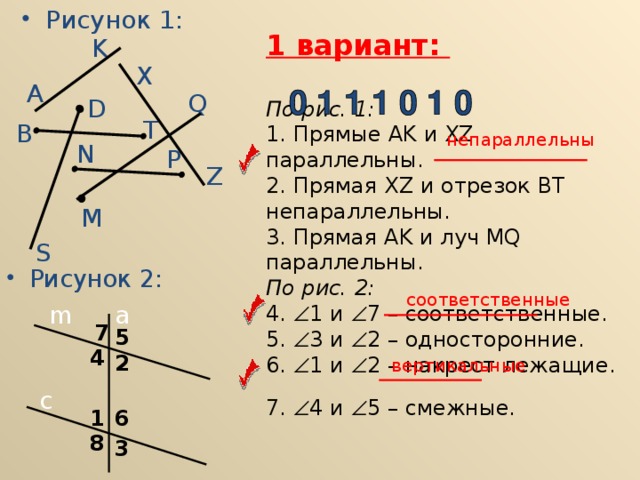
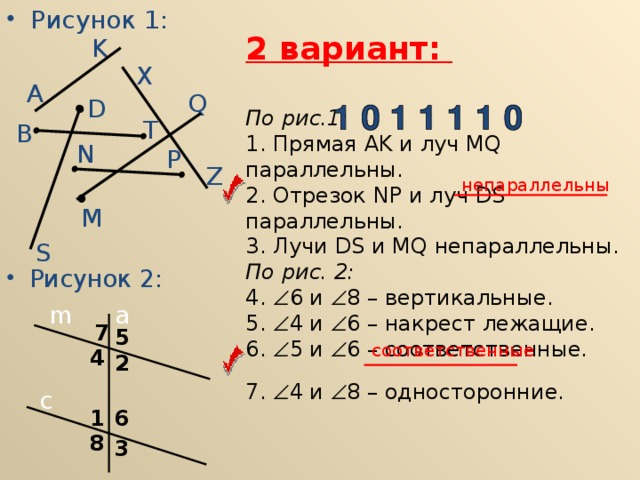
•Рисунок 1:
Тест
Ответы к тесту
Вычеркнуть лишние слова в скобках:
Аксиома – это (очевидные, принятые, исходные) положения геометрии,
не требующие (объяснений, доказательств, обоснований).
2) Выбрать окончание формулировки аксиомы параллельных прямых:
Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) только одна прямая, не пересекающаяся с данной.
3) Что может быть следствием аксиомы или теоремы? Указать неверные ответы.
а) Утверждение, не требующее доказательства.
б) Новая теорема, для доказательства которой использована аксиома
или теорема.
в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
Вычеркнуть лишние слова в скобках:
Аксиома – это (очевидные, принятые, исходные) положения геометрии,
не требующие (объяснений, доказательств, обоснований).
2) Выбрать окончание формулировки аксиомы параллельных прямых:
Через точку, не лежащую на данной прямой, проходит:
а) только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) только одна прямая, не пересекающаяся с данной.
3) Что может быть следствием аксиомы или теоремы? Указать неверные ответы.
а) Утверждение, не требующее доказательства.
б) Новая теорема, для доказательства которой использована аксиома
или теорема.
в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
4) Указать следствия аксиомы параллельных прямых.
а) Если отрезок или луч пересекает одну из параллельных прямых,
то он пересекает и другую.
б) Если две прямые параллельны третьей прямой,
то они параллельны друг другу.
в) Если прямая пересекает одну из параллельных прямых,
то она пересекает и другую.
г) Если три прямые параллельны,
то любые две из них параллельны друг другу.
д) Если две прямые не параллельны третьей прямой,
то они не параллельны между собой.
е) Если прямая пересекает одну из параллельных прямых,
то она не может не пересекать другую.
ж) Если две прямые параллельны третьей прямой,
то они не могут быть не параллельны между собой.