Данная презентация предназначена для проведения урока по теме "Теорема Пифагора" в геометрии 8 класса. Представленный материал содержит несколько формулировок теоремы,, различные способы её доказательства, интересные факты из истории возникновения, а также занимательный материал. Данная работа интересна ученикам, так как составлена доступным для них языком, поэтому она легко воспринимается. В учебнике "Геометрия-8" представлен лишь один способ доказательства, но после просмотра презентации некоторые ученики задаются целью отыскать другие способы доказательства и попробовать разобраться в них.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
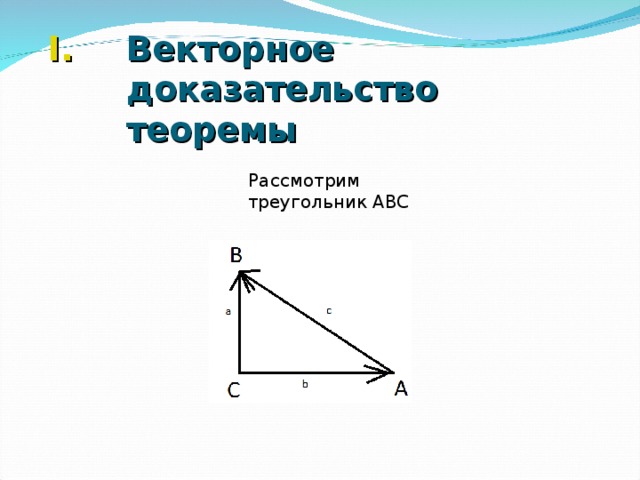
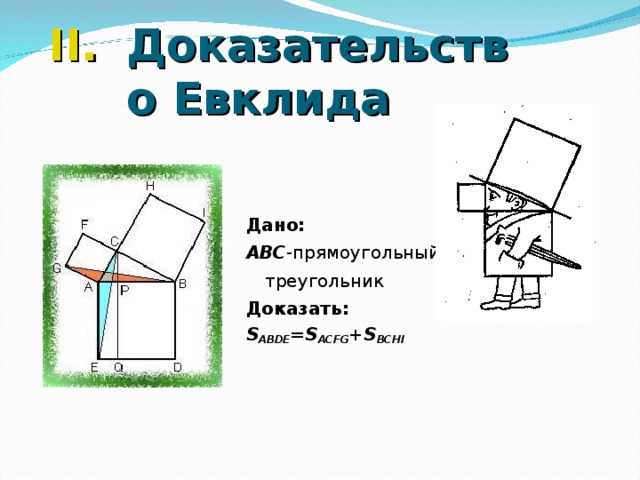
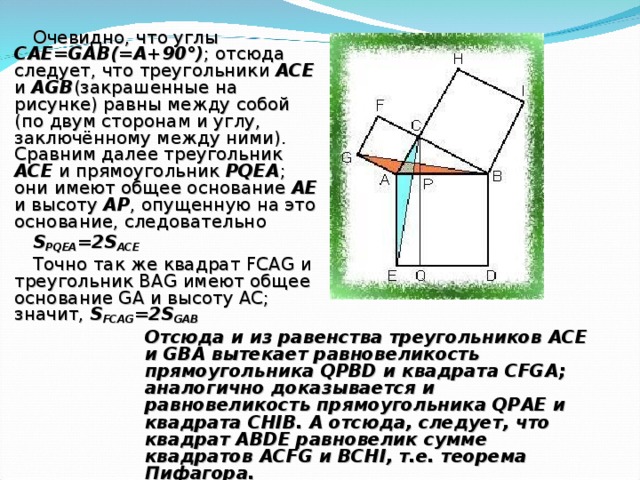
Презентация к уроку геометрии по теме "Теорема Пифагора"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к уроку геометрии по теме "Теорема Пифагора" »
Полезное для учителя
Распродажа видеоуроков!
2230 руб.
3190 руб.
2100 руб.
3000 руб.
2220 руб.
3170 руб.
1230 руб.
1760 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства