Презентация к уроку геометрии "Фигуры вращения"

III. Повторение основных сведений о конусе
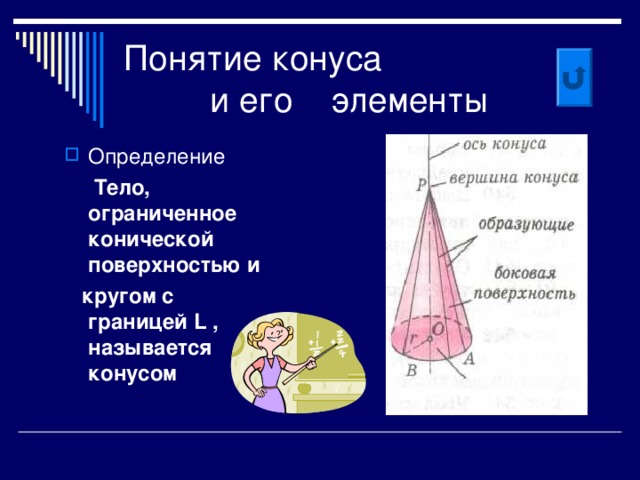
- Определение конуса
- Элементы конуса
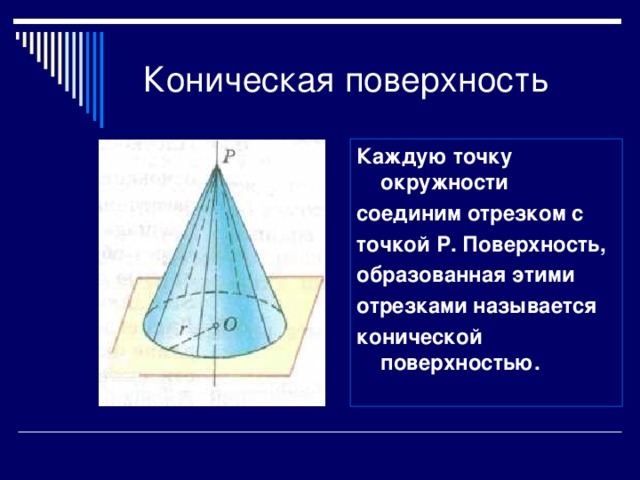
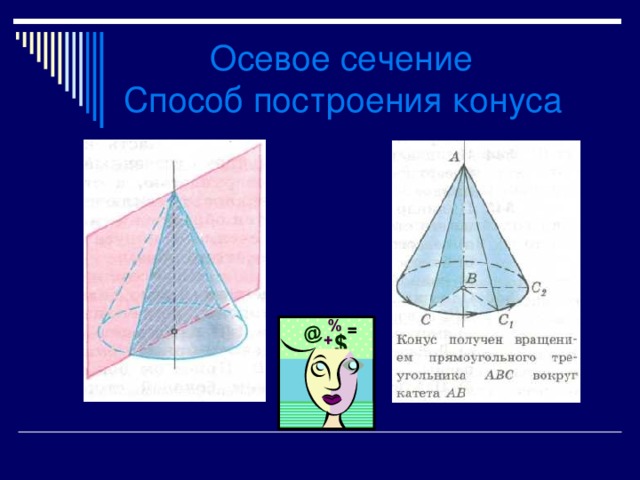
- Сечения конуса
- Площадь поверхности конуса.
^ IV. Историческая справка.
Конус в переводе с греческого означает « сосновая шишка ». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда ( 287 – 212 гг. до н.э. ) « О методе » , в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470 – 380 гг. до н.э.) –древне-греческому философу-материалисту. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона ( 428 – 348 гг. до н.э. ) Платон был учеником Сократа ( 470 – 399 гг. до н.э. ). Он в 387 г. до н.э. основал в Афинах Академию, в которой работал 20 лет. Каждый, входящий В Академию, читал надпись : « Пусть сюда не входит никто, не знающий геометрии». Школе Платона принадлежит исследование свойств призмы, цилиндра и конуса; изучение конических сечений.
Большой трактат о конических сечениях принадлежит Аполлонию Пергскому (260 – 170 гг. до н.э. ) – ученику Евклида ( III в. до н.э. ), который создал великий труд из 15 книг под названием « Начала». В ХII книге «Начал» Евклида содержатся следующие теоремы:
1) Объем конуса равен одной трети объема цилиндра с равным основанием и равной высотой; доказательство этой теоремы принадлежит Евдоксу Книдскому.

2) Отношение объемов двух конусов с равными основаниями равно отношению соответствующих высот.

3) Если два конуса равновелики, то площади их оснований обратно пропорциональны соответствующим высотам и наоборот.

Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор. Непосредственное вычисление объема конуса дает Герон Александрийский.
^ V. Объяснение нового материала :
Предложить учащимся на основе имеющихся знаний вывести формулу для нахождения объема конуса.( учащиеся могут предложить различные способы для вычисления: через определенный интеграл, предел и рассмотреть конус как тело вращения прямоугольного треугольника вокруг катета. Если же они сами не смогут выполнить задание, то рассматривается материал по рассказу учителя с привлечением учащихся).
1 способ : Для вывода формулы объема конуса воспользуемся основной формулой для вычисления объемов тел с помощью определенного интеграла
Рассмотрим конус, у которого радиус основания r, высота h. Введем ось ОХ с началом в вершине конуса, вдоль его оси, и проведем произвольное сечение конуса плоскостью, перпендикулярной к оси ОХ.
Дальнейшие рассуждения аналогичны тем, что мы использовали при выводе объема пирамиды. (Для продолжения доказательства к доске приглашается ученик.) Получаем :
2 способ: Эту же формулу можно получить используя предел к которому стремится объем правильной пирамиды, вписанной в конус, при неограниченном увеличении числа сторон ее основания.V = V=
3 способ: Эту же самую формулу можно получить, рассматривая конус как тело вращения прямоугольного треугольника вокруг катета.
Проведите доказательство самостоятельно.
Как правило, несколько учеников быстро справляются с заданием и один из них записывает вывод формулы на доске.)

.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Презентация к уроку геометрии "Фигуры вращения" »

Фигуры вращения

Презентация учителя

МБОУ «СОШ №4» с.Волжское

Наримановского района

Кулисовой Р.С.

Коническая поверхность

Каждую точку окружности

соединим отрезком с

точкой Р. Поверхность,

образованная этими

отрезками называется

конической поверхностью.

Понятие конуса и его элементы

Определение

Тело, ограниченное конической поверхностью и

кругом с границей L , называется конусом

Конус по Далю

м . тело в виде сахарной головы, круглый клин: правильный конус образуется от обращенья прямоугольного треугольника вокруг одной из коротких сторон, как около оси; если конец неподвижного вверху отвеса обвести по окружности круга, то отвес очертит конус. Конусный, к конусу относящ. Конический, коноидальный, конусовидный, -подобный, -образный, или конусоватый, видом, очерком похожий на конус. Конические сечения, кривые разных, замечательных математических свойств, образующиеся на поверхности конуса, от пересеченья ею плоскостямя. Сеченье поперек, равнобежно основанью, дает круг; сеченье отвесное, гиперболу; поперечное, но косвеное, элипс, долгий круг; косое же, но сверху вниз и равнобежное боку конуса, параболу. Коноид м. тело, очерченое кривою чертою, обратившеюся вкруг оси своей, и пр. элипсоид, гиперболоид, пароболоид и пр. тела коноидальные, коноиды.

Конус по Ожигову

Геометрическое тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов

Историческая справка

В переводе с древнегреческого « konos » означает « сосновая шишка ». С конусом люди были знакомы с глубокой древности.

В 1906 г. была обнаружена книга Архимеда

«О методе», в которой дается решение

задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает

честь этого открытия Демокриту.

С ее помощью Демокрит получил формулы для

вычисления объема пирамиды и конуса.

«Пусть сюда не входит никто, не знающий геометрии»

Много сделала для геометрии и школа Платона. Платон был учеником Сократа и в

387 г до н.э. основал в Афинах Академию.

Каждый входящий в Академию читал

надпись: «Пусть сюда не входит никто, не

знающий геометрии».

Сечения конуса

Сечение конуса плоскостью а, перпендикулярной к его оси, — круг с центром O 1 радиуса r 1= PO 1

PO r

Осевое сечение Способ построения конуса

Самостоятельная работа

Высота конуса равна 15см, а радиус основания равен 6 см. Найдите образующую конуса.
Образующая конуса, равная 10 см, наклонена к плоскости основания под углом 45. Найти площадь основания конуса.
Осевое сечение конуса – прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 4 см.
Найдите высоту конуса, если площадь его осевого сечения равна 6 дм, а площадь основания 8 дм.

Дополнительная информация о конусе

В геологии существует

понятие «конус выноса».

Это форма рельефа,

образованная скоплением

обломочных пород (гальки,

песка), вынесенная горными

реками в предгорную долину

Конус в физике

По статистике на Земле ежегодно

гибнет от разрядов молнии 6 чел.

на 1млн жителей (чаще в южных

странах). Этого не случилось,

если бы везде были Громо-

отводы, т.к. образуется пояс

безопасности. Чем выше

громоотвод, тем больше

охват такого конуса.

«Конус удивления и прочие фигуры»

Почти все предметы, составляющие натюрморты, реальны - куб, шар, конус - за исключением "Конуса удивления". Это придуманная, авторская фигура. Встретив натюрморт этого цикла в Италии например, Южной Америке или Канаде его можно сразу узнать и сказать безошибочно - "Борис Лаврентьев - "Конус удивления и прочие фигуры" ".

Туманность Конус

Пояснение: Конусы, столбы и величественные потоки можно в большом количестве найти в звездных яслях , где облака газа и пыли подвергаются воздействию мощных ветров недавно родившихся звезд. Хорошо известный пример - туманность Конус , входящая в яркую галактическую область звездообразования NGC 2264. Ее изображение крупным планом было получено новейшей камерой Космического телескопа Хаббла. В то время как туманность Конус, находящаяся на расстоянии 2500 световых лет в созвездии Единорог, имеет длину около 7 световых лет, показанная здесь область около затупленной вершины конуса имеет в поперечнике всего 2.5 световых года..

Пояснение: Конусы, столбы и величественные потоки можно в большом количестве найти в звездных яслях , где облака газа и пыли подвергаются воздействию мощных ветров недавно родившихся звезд. Хорошо известный пример - туманность Конус , входящая в яркую галактическую область звездообразования NGC 2264. Ее изображение крупным планом было получено новейшей камерой Космического телескопа Хаббла. В то время как туманность Конус, находящаяся на расстоянии 2500 световых лет в созвездии Единорог, имеет длину около 7 световых лет, показанная здесь область около затупленной вершины конуса имеет в поперечнике всего 2.5 световых года..

В нашей области Галактики это расстояние составляет немногим более половины пути от Солнца до ближайшей звезды - Альфа Центавра. Массивная звезда NGC 2264 IRS, которая была обнаружена инфракрасной камерой телескопа Хаббла в 1997 г., скорее всего являющаяся источником ветра, придающем форму туманности Конус, находится за верхним краем этого изображения. Красноватое свечение туманности Конус создается излучением водорода.

В нашей области Галактики это расстояние составляет немногим более половины пути от Солнца до ближайшей звезды - Альфа Центавра. Массивная звезда NGC 2264 IRS, которая была обнаружена инфракрасной камерой телескопа Хаббла в 1997 г., скорее всего являющаяся источником ветра, придающем форму туманности Конус, находится за верхним краем этого изображения. Красноватое свечение туманности Конус создается излучением водорода.

Практическое задание

По модели конуса найдите:

а) высоту;

б) радиус основания;

в) образующую;

г) площадь основания;

д) площадь боковой поверхности;

е) площадь полной поверхности.

Проблемные вопросы

Какая фигура получится при вращении прямоугольного равнобедренного треугольника вокруг меньшей высоты?
В каких границах может изменятся угол при вершине осевого сечения?
Угол при вершине осевого сечения конуса -- прямой. Во сколько раз площадь основания конуса больше площади осевого сечения?
Во сколько раз площадь боковой поверхности равностороннего конуса больше площади его основания?