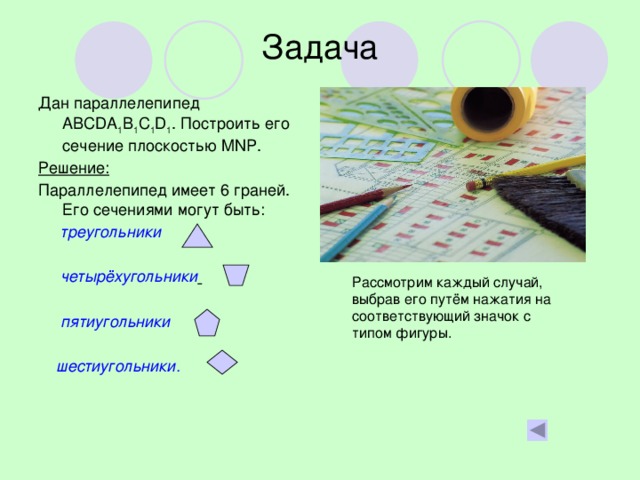
Презентация «Построение сечений параллелепипеда» выполнена с использованием анимационных эффектов.
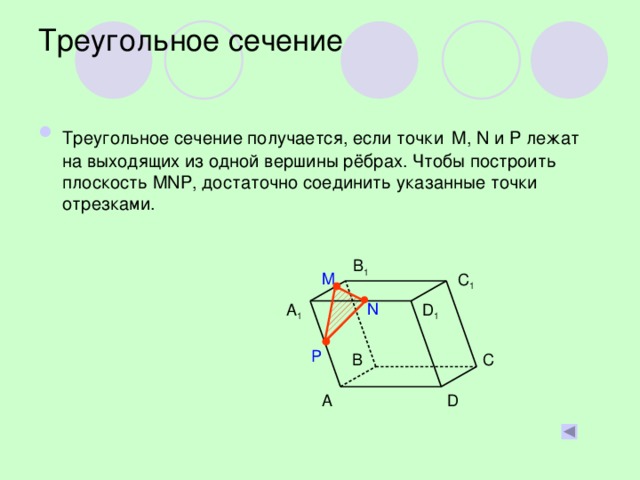
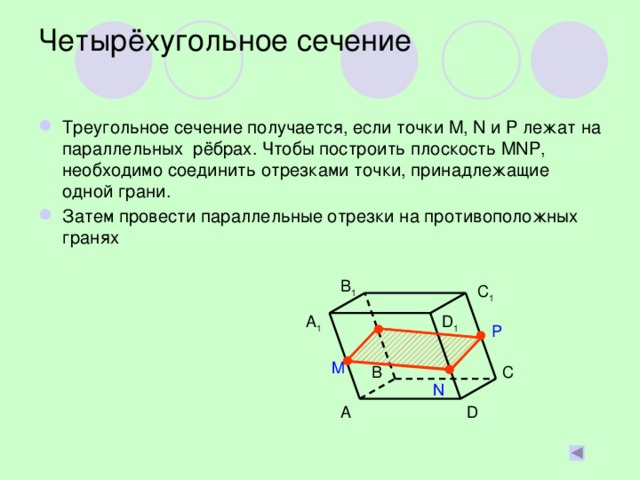
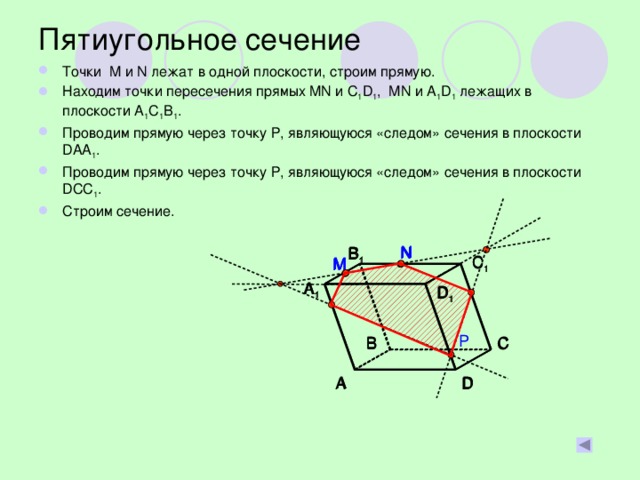
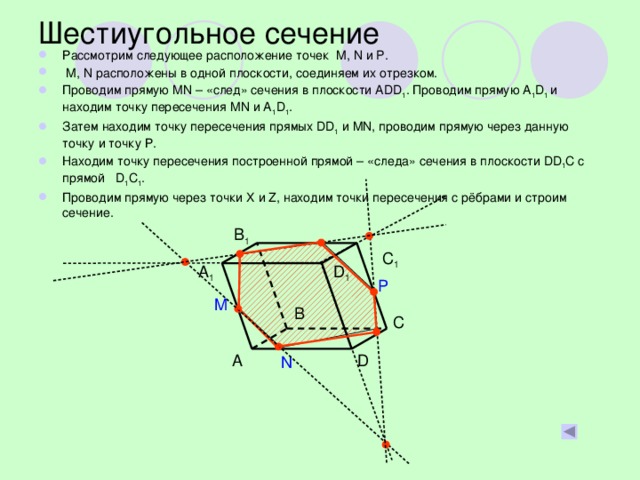
В презентации последовательно демонстрируются и описываются этапы построения сечений наклонного параллелепипеда.
Данная презентация предназначена как для учителя математики и может быть использована при объяснении нового материала на уроках геометрии, так и для учеников старших классов, желающих самостоятельно изучить данную тему, повторить и закрепить её.
Может быть использована при дистанционном обучении.