Урок обобщения темы "Показательная функция". Содержит материал для проведения самостоятельной работы и дифференцированной работе на уроке. Разные виды показательных уравнений и неравеств. Готовит учащихся к предстоящей контрольной работе по теме "Показательная функция. Решение показательных уравнений и неравеств"
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Показательная функция. Решение показательных уравнений и неравенств.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Показательная функция. Решение показательных уравнений и неравенств. »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2230 руб.
3190 руб.
1790 руб.
2560 руб.
2220 руб.
3170 руб.
1570 руб.
2240 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

 0, а ≠ 1, х – показатель степени), называется показательной функцией с основанием а." width="640"
0, а ≠ 1, х – показатель степени), называется показательной функцией с основанием а." width="640"
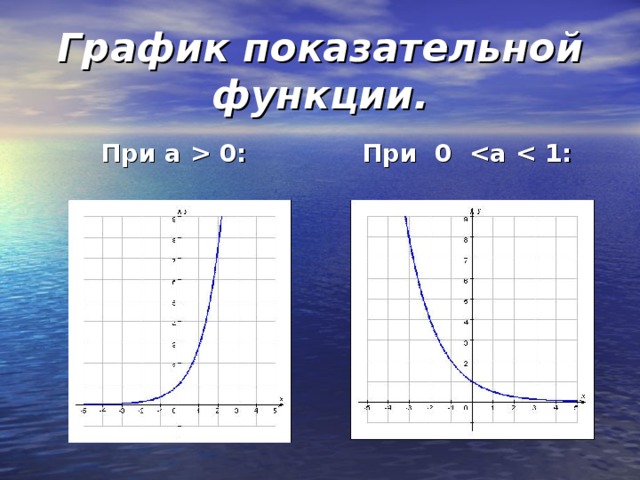 0:" width="640"
0:" width="640"
 0: при 0" width="640"
0: при 0" width="640"
 1, 0" width="640"
1, 0" width="640"




 0, находим у 1 = 4, у 2 = – 6. Получаем два уравнения: 2 х = 4 и 2 х = – 6 2 2 = 2 2 корней нет. х = 2. Путем введения новой переменной приводят уравнение к квадратному ." width="640"
0, находим у 1 = 4, у 2 = – 6. Получаем два уравнения: 2 х = 4 и 2 х = – 6 2 2 = 2 2 корней нет. х = 2. Путем введения новой переменной приводят уравнение к квадратному ." width="640"
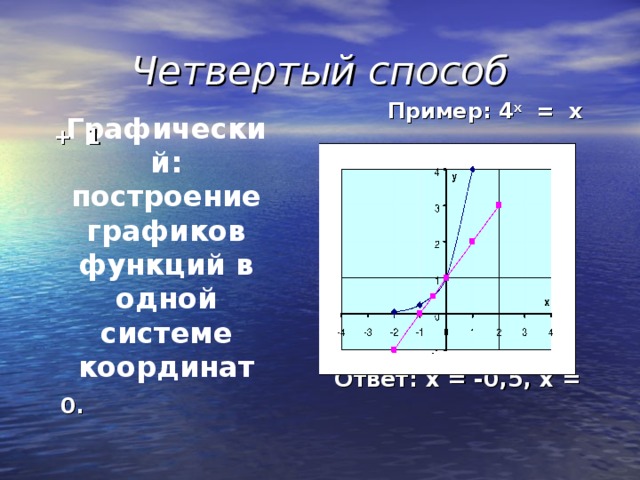


 а g(x) , где а – положительное число, отличное от нуля, и неравенства, сводящиеся к этому виду f ( x ) q ( x )." width="640"
а g(x) , где а – положительное число, отличное от нуля, и неравенства, сводящиеся к этому виду f ( x ) q ( x )." width="640"
 0, Если 0 то показательное неравенство а f (x) а g (x) равносильно неравенству того же смысла f ( x ) q ( x ). то показательное неравенство а f (x) а g (x) равносильно неравенству противоположного смысла f ( x )" width="640"
0, Если 0 то показательное неравенство а f (x) а g (x) равносильно неравенству того же смысла f ( x ) q ( x ). то показательное неравенство а f (x) а g (x) равносильно неравенству противоположного смысла f ( x )" width="640"
 64 2 2х-4 2 6 2х – 4 6 2х 10 х 5 Ответ: х 5 (0,2) х ≥ 0,04 (0,2) х ≥ (0,2) 2 х ≤ Ответ: х ≤ 2" width="640"
64 2 2х-4 2 6 2х – 4 6 2х 10 х 5 Ответ: х 5 (0,2) х ≥ 0,04 (0,2) х ≥ (0,2) 2 х ≤ Ответ: х ≤ 2" width="640"
 0,027 3. 2 х + 2 х+2 4. 11 2х+3 ≥ 121 5. 5 4х+2 ≤ 125" width="640"
0,027 3. 2 х + 2 х+2 4. 11 2х+3 ≥ 121 5. 5 4х+2 ≤ 125" width="640"
















