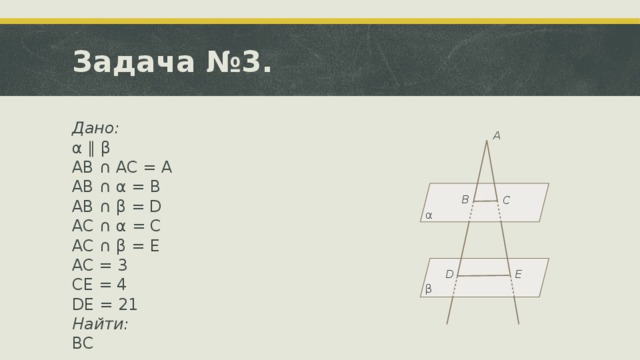
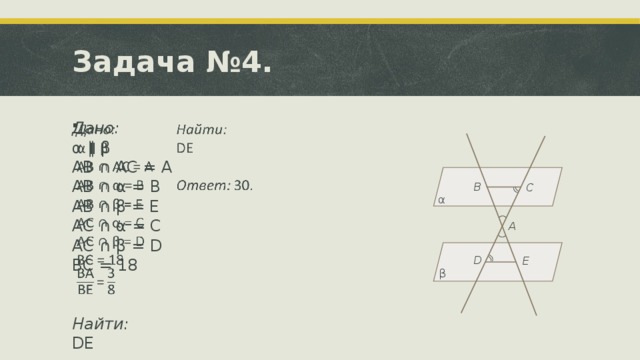
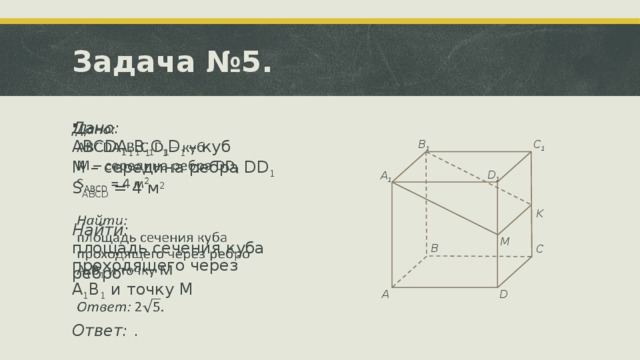
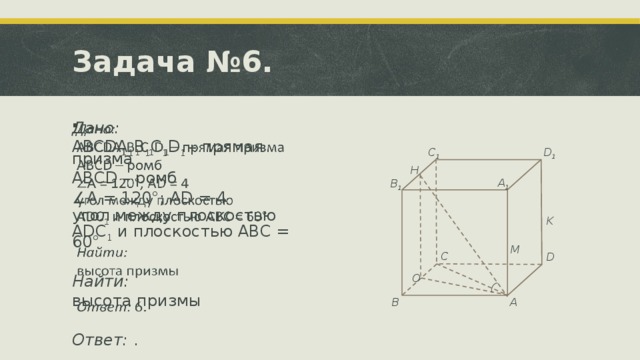
Данная презентация подготовлена для проведения урока по темам "Параллельность прямой и плоскости" и "Параллельность плоскостей". В ней представлен теоретический материал (определения, теоремы, свойства) и задачи для практического применения. Задачи предполагают решение в классе или могут быть предложены (как и вся презентация)уч ащимся для домашней работы, так как к ним предлагаются подсказки и ответы, а не полностью разобранные решения. В конце работы для учащихся составлена самостоятельная работа состоящая из двух вариантов по четыре задачи в каждом.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Параллельность прямых и плоскостей.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Параллельность прямых и плоскостей.»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
1630 руб.
2330 руб.
2220 руб.
3170 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства