Обобщение и систематизация "Призмы"

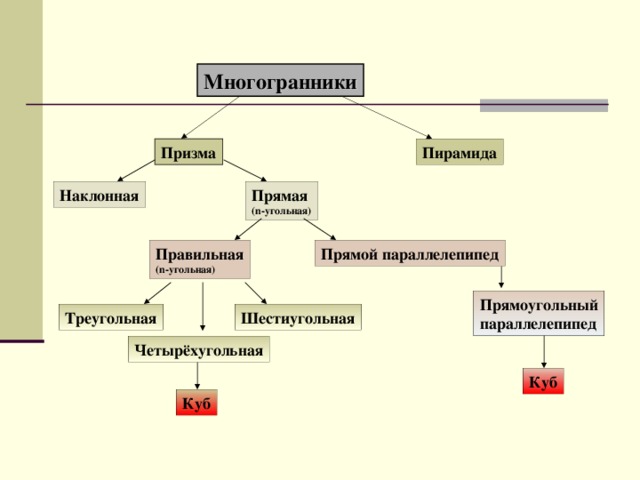
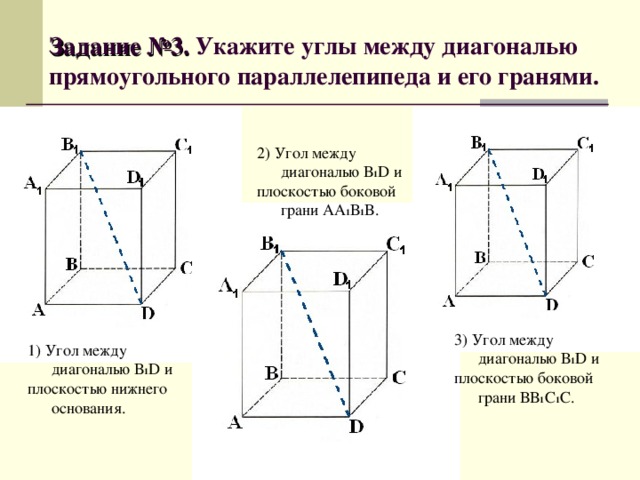
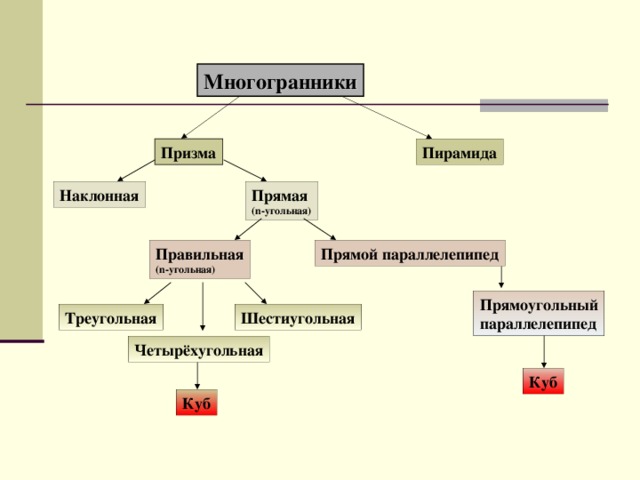
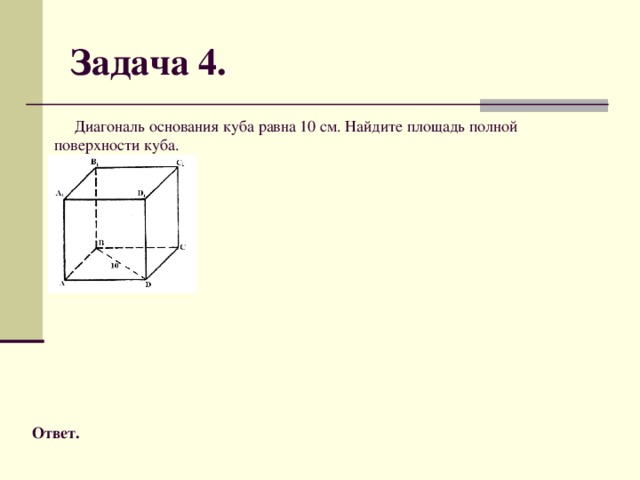
В данной работе рассмотрены вопросы:свойства призмы, формулы для вычисления основных параметров призмы, практическое применение призмы и формул для вычисления площадей боковой и полной поверхности призмы.Актуализация опорных знаний, умений рассмотрена в виде тестовых заданий на соответствие между определениями многогранников, его свойствами и формулами площадей боковой и полной поверхности многогранника. Особое внимание уделено нахождению угла между диагональю прямоугольного параллелепипеда и его гранями.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Обобщение и систематизация "Призмы" »

3 декабря

Классная работа

Систематизация и обобщение темы: «Призма»

Свойства призмы. Формулы для вычисления основных параметров и их практическое применение.

Учитель Леус Анна Фёдоровна

Актуализация опорных знаний и умений

Задание №1

Найдите соответствие:

1). Призма, все грани которой – параллелограммы называется ...

2). Прямоугольный параллелепипед с равными рёбрами называется ...

3). Прямая призма, основания которой – квадраты называется ...

4). Прямой параллелепипед, все грани которого – прямоугольники называется ...

А) Куб

Б) Правильная призма

В) Наклонный параллелепипед

Г) Прямоугольный параллелепипед

Ответы.

1). В

2). А

3). Б

4). Г

Многогранники

Пирамида

Призма

Прямая

(n-угольная)

Наклонная

Прямой параллелепипед

Правильная

(n-угольная)

Прямоугольный

параллелепипед

Шестиугольная

Треугольная

Четырёхугольная

Куб

Задание №2

Назовите формулы:

Площадь полной поверхности куба
Площадь боковой поверхности прямоугольного параллелепипеда
Площадь боковой поверхности наклонной призмы

4) Площадь полной поверхности правильной треугольной призмы, если а – сторона основания, Н – высота.

S п = 6 а ²

S б = Р осн. *Н

Sб = Рперп.сеч.*АА1, АА1 – боковое ребро

Sб = Росн. * Н

S п = S б + 2 S осн .

S п = 3а *Н +

а² √ 3

Задание №3. Укажите углы между диагональю прямоугольного параллелепипеда и его гранями.

2) Угол между диагональю В 1 D и

плоскостью боковой грани АА 1 В 1 В.

3) Угол между диагональю В 1 D и

плоскостью боковой грани ВВ 1 С 1 С.

1) Угол между диагональю В 1 D и

плоскостью нижнего основания.

Защита проектов по теме: “Призма”

Многогранники

Пирамида

Призма

Прямая

(n-угольная)

Наклонная

Прямой параллелепипед

Правильная

(n-угольная)

Прямоугольный

параллелепипед

Шестиугольная

Треугольная

Четырёхугольная

Куб

Тренировочные задачи

1) Вычислите высоту и площадь основания правильной четырёхугольной призмы, если площадь диагонального сечения равна 30 см ², а диагональ основания 5 см.

2) В прямоугольном параллелепипеде стороны основания равны 6 см и 8 см. Высота параллелепипеда равна 12 см. Найдите площадь диагонального сечения.

3) В основании прямого параллелепипеда лежит ромб с диагоналями 12 см и 16 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45°. Найдите площадь полной поверхности.

4) Диагональ основания куба равна 10 см. Найдите площадь полной поверхности куба.

Задача 1.

Вычислите высоту и площадь основания правильной четырёхугольной призмы , если площадь диагонального сечения равна 30 см², а диагональ основания 5 см.

Ответ.

Задача 2.

В прямоугольном параллелепипеде стороны основания равны 6 см и 8 см. Высота параллелепипеда равна 12 см. Найдите площадь диагонального сечения.

Ответ.

Задача 3.

В основании прямого параллелепипеда лежит ромб с диагоналями 12 см и 16 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол 45°. Найдите площадь полной поверхности.

Ответ.

Задача 4.

Диагональ основания куба равна 10 см. Найдите площадь полной поверхности куба.

Ответ.

Предмет: Математика

Категория: Презентации

Целевая аудитория: 11 класс

Скачать
Обобщение и систематизация "Призмы"

Автор: Леус Анна Федоровна,Кучер Людмила Викторовна

Дата: 27.01.2015

Номер свидетельства: 162662

Похожие файлы

Конспект урока по физике "Кристаллические и аморфные тела"

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(108) "Конспект урока по физике "Кристаллические и аморфные тела" "
    ["seo_title"] => string(63) "konspiekt-uroka-po-fizikie-kristallichieskiie-i-amorfnyie-tiela"
    ["file_id"] => string(6) "139917"
    ["category_seo"] => string(6) "fizika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1417832587"
  }
}

Открытый интегрированный урок – конференция, практикум по теме: «Геометрические тела и их объём».

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(182) "Открытый интегрированный урок – конференция, практикум по теме: «Геометрические тела и их объём». "
    ["seo_title"] => string(105) "otkrytyi-intieghrirovannyi-urok-konfierientsiia-praktikum-po-tiemie-gieomietrichieskiie-tiela-i-ikh-obiom"
    ["file_id"] => string(6) "182024"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1425455390"
  }
}

План – конспект открытого интегрированного урока- конференции, практикума по геометрии на 2 курсе в группе № 15

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(205) "План – конспект  открытого интегрированного урока- конференции, практикума по геометрии на 2 курсе в группе № 15 "
    ["seo_title"] => string(119) "plan-konspiekt-otkrytogho-intieghrirovannogho-uroka-konfierientsii-praktikuma-po-ghieomietrii-na-2-kursie-v-ghruppie-15"
    ["file_id"] => string(6) "229515"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1441767341"
  }
}

Формирование информационной компетентности учащихся на уроках геометрии

object(ArrayObject)#875 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(138) "Формирование информационной компетентности  учащихся на уроках геометрии "
    ["seo_title"] => string(85) "formirovaniie-informatsionnoi-kompietientnosti-uchashchikhsia-na-urokakh-ghieomietrii"
    ["file_id"] => string(6) "168793"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1423303396"
  }
}

Программа спецкурса по математике " Математика абитуриенту",11 класс

object(ArrayObject)#853 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(125) "Программа спецкурса по математике " Математика абитуриенту",11 класс "
    ["seo_title"] => string(72) "proghramma-spietskursa-po-matiematikie-matiematika-abituriientu-11-klass"
    ["file_id"] => string(6) "118819"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1413266581"
  }
}

Обобщение и систематизация "Призмы"

Просмотр содержимого документа «Обобщение и систематизация "Призмы" »

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Обобщение и систематизация "Призмы" »