"Нестандартные способы умножения"

«Нестандартные способы умножения»

(занятие математического кружка, 5-6 класс)

Автор: Будко Любовь Фёдоровна – учитель математики МБОУ СОШ №1 х. Маяк Сальского района Ростовской области.

Автор: Будко Любовь Фёдоровна учитель

математики МБОУСОШ № 1 х.Маяк,

Сальский район, Ростовская область.

2014 год.

Аннотация

Каждый школьник умеет умножать многозначные числа «столбиком».

И каждый считает, что это скучные вычислительные действия. Однако существуют и другие интересные способы, которые могут «нудные» вычисления превратить в весёлую игру.

В этой работе представлено одно из занятий математического кружка, на котором изучаются нестандартные способы умножения.

Тема: «Нестандартные способы умножения».

Разработка занятия основана на многолетнем личном опыте работы по проведению занятий кружка «За страницами учебника математики». Материал (конспект занятия и авторская презентация) предназначен для учителей математики. Он может изучаться на занятиях кружка, уроках математики, факультативно и различных внеклассных мероприятиях (для 5-6 классов).

Занятие построено так, что большую часть знаний ученики получают в процессе самостоятельного поиска путем решения поисковых задач, соответствующих их возрасту, и при использовании соответствующих способов деятельности. На занятии имеет место систематический контроль качества усвоения знаний учащимися.
Предлагаемый материал может использоваться также школьниками в их самостоятельной творческой деятельности с целью повышения вычислительной культуры. Вычислительная культура высокого уровня для современного школьника-это гарантия успешности при выполнении контрольных работах, при сдаче ГИА и ЕГЭ, т.к. ни в одной из ситуаций не предусмотрено применение калькулятора.

Использование презентации создаёт условия для повышения продуктивности обучения (так как увеличивается объем изучаемого материала при уплотнении временных рамок), способствует усилению наглядности материала (делает материал более интересным для любого ученика с разной мотивацией к учению).

Содержание

Автор: Будко Любовь Фёдоровна, учитель математики высшей категории.

Образовательное учреждение: Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 х. Маяк Сальского района Ростовской области.

Предмет: математика

Класс: 5-6 классы

Уровень образования школьников: базовый уровень общего образования.

Тема: « Нестандартные способы умножения».

Тип занятий: занятия кружка

Необходимое время: 2 академических часа: 40мин. - первая часть занятия,10 мин.- перерыв, 40 мин. – вторая часть занятия.

Основные цели материала:

-расширение кругозора учащихся путём изучения новых методов решения;

- вовлечение в деятельность на занятиях каждого ученика;

- демонстрация красоты предмета и практической значимости .

Задачи:

образовательные:

- изучить некоторые старинные способы умножения столбиком;

-изучить способы умножения без таблиц умножения и научить их применять.

Развивающие:

-развивать познавательную активность, творческие способности, мышление, умение анализировать и обобщать, переносить знания из одной ситуации в другую;

-учить искать, извлекать, систематизировать, отбирать необходимую для решения учебных задач информацию из учебника и дополнительной литературы, преобразовывать, и применять её.

Воспитательные:

вызвать интерес к практическому применению полученных знаний по теме, формировать навыки взаимоконтроля, самоконтроля и самооценки. Воспитывать культуру общения, умение работать в парах, группах, слушать друг друга, воспитывать чувство взаимовыручки, внимательного отношения друг к другу при работе на уроке.
Методы обучения:

проблемно-поисковый, исследовательский, коммуникативный, информационный.

Форма организации работы учащихся: индивидуальная, самостоятельная, работа в парах, группах.

Формы и приёмы контроля: самоконтроль, взаимоконтроль, дискуссия, диагностика.

Оборудование:

персональные компьютеры, подключенные к сети Internet, принтер, мультимедийный проектор, экран, рабочая тетрадь.

Обоснование выбора темы

В пятых-шестых  классах очень важно не только дать детям твердые знания начал математики, но и увлечь их этим предметом. Хорошо развитые у учащихся навыки устного счета - одно из условий их успешного обучения в старших классах. В учебной программе базового курса математики в 5-6 классах даётся мало времени на изучение нестандартных способов умножения. Поэтому я убеждена в полезности знакомства с темами:

1.Старинные способы умножения.

2.Способы умножения чисел без таблицы умножения.

Научная новизна и практическая значимость работы заключается в подборе материала по теме, не изучаемой в школьном курсе математики.

Понимание предлагаемого материала не требует специальных знаний, выходящих за пределы программы по математике основной школы.

Однако его актуальность заключается в том, что он вызывает интерес, способствует развитию в учениках инициативы в познавательной деятельности, наблюдательности и любознательности, даёт возможность расширить свои знания, повышает вычислительную культуру.

Ожидаемые результаты

В результате изучения этих тем учащиеся могут научиться:

- выполнять умножение многозначных чисел с применением одного из старинных способов, или, наоборот, оценить универсальность, компактность и рациональность нашего современного способа умножения «столбиком».

- выполнять умножение многозначных чисел устно с применением нестандартных способов умножения, что будет способствовать повышению вычислительной культуры учеников.

Цель использования ИКТ:

- создание условий для повышения продуктивности обучения (так как увеличивается объем изучаемого материала при уплотнении временных рамок);

- усиление наглядности материала (делает материал более интересным для любого ученика с разной мотивацией к учению)

План занятий

№п/п	Этап занятия	Время в минутах
I	Первая часть занятия	40мин
1	Организационный момент	2
2	Выступления кружковцев	20
3	Первичная проверка понимания школьниками учебного материала	10
4	Дискуссия, ответы на вопросы	6
5	Выводы	2
	Перерыв	10
II	Вторая часть занятия	40 мин
1	Умножение с помощью рисунков	14
2	Умножение на 101,1001,...	6
3	Умножение на 11	7
4	Умножение на 111,1111,…	8
5	Выводы	2
6	Рефлексия, выставление оценок	2
7	Домашнее задание	1

Ход занятий

Первая часть занятия.

1.Учитель обращается к кружковцам: «На предыдущем занятии вы были разделены на группы. За каждой группой был закреплён консультант – старшеклассник, который помогал оформить слайд к презентации. Каждая группа получила творческое задание: изучить один из старинных способов умножения столбиком. При подготовке можно было воспользоваться не только рекомендованными источниками информации.

Тема: «Несколько старинных способов умножения столбиком».[2,3]

Содержание:

«Малый замок»(слайд 6).

«Ревность» (слайд7).

Русский крестьянский способ (слайд 8).

Индийский способ (слайд 10).

Арабский способ (слайд 11)

2-3. Выступают представители от каждой группы, которые рассказывают об изученном способе умножения.

«Малый замок» ( слайд 6)

Итальянский учёный конца XV века Лука Пачиоли в трактате об арифметике приводит 8 различных способов умножения. В первом, который носит название «маленький замок», цифры верхнего числа, начиная со старшей, поочерёдно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.

«Ревность»(слайд 7)

Рисуется решётка, в которую затем вписывают результаты промежуточных вычислений, точнее, числа из таблицы умножения. Решётка является прямоугольником, разделённым на квадратные клетки, которые, в свою очередь, разделены пополам диагоналями.

Слева (снизу вверх) писался первый множитель, а наверху – второй. На пересечении соответствующей строки и столбца писалось произведение стоящих в них цифр. Затем полученные числа складывались вдоль проведённых диагоналей, а результат записывался в конце такого столбика. Результат прочитывался вдоль нижней и правой сторон прямоугольника.

Русский крестьянский способ( слайд 8)

Чтобы перемножить два числа, их записывали рядом, а затем правое число делили на 2, а левое умножали на 2. В те давние времена удвоение и раздвоение принимались даже за особые арифметические действия.

Если множимое не делится на 2, то от него сначала отнимается единица, а затем уже производится деление на 2. Строчки с чётными множимыми вычёркиваются, а правые части строчек с нечётными множимыми складываются.

Индийский способ(слайд 10)

Индийским способом можно было бы умножать, начиная и с единиц. Однако сами индийцы умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры.

Арабский способ (слайд 11)

В отличии от индийского способа, ненужные цифры не стираются (на бумаге это делать уже неудобно), а вычёркиваются. Новые цифры записываются над зачёркнутыми, разумеется, поразрядно. Арабский способ умножения не очень-то удобен. Тем не менее, этот способ умножения держался в Европе вплоть до восемнадцатого века, целых тысячу лет. Он назывался способом крестика, или хиазмом, так как между перемножаемыми числами ставилась греческая буква Х (хи), постепенно заменённая косым крестом.

После каждого выступления.

Ученики:

-задают вопросы, на которые может отвечать каждый член выступавшей группы;

-пытаются выполнить умножение по аналогии с целью первичной проверки понимания нового учебного материала.

Учитель:

- корректирует выступления;

-руководит дискуссией;

- с целью экономии времени раздаёт каждому ученику готовый рисунок «Решётки». (См. приложение).

4.После всех выступлений.

Учитель просит детей:

- ответить на вопросы (слайд 12);

-сделать вывод.

5. Школьники:

- старинные способы умножения интересны, занимательны, но использовать их на практике не всегда удобно и рационально;

- хотелось бы познакомиться с такими правилами, которые избавляют от умножения «столбиком», а, возможно, и от таблиц умножения.

Учитель: « После перерыва мы изучим некоторые способы умножения без таблиц».

Вторая часть занятия - работа в парах. (Условие работы: дети в парах выступают по очереди, что обеспечивает максимальную активность каждого).

Тема: «Умножение без таблиц».

Содержание:

Умножение с помощью рисунков (слайды 14-18). [4]

Умножение чисел на 101,1001...(слайд 19).[5]

Умножение чисел на 11 (слайды 20-21). [6, 2]

Умножение чисел на 111… (слайды 22-23). [6, 2]

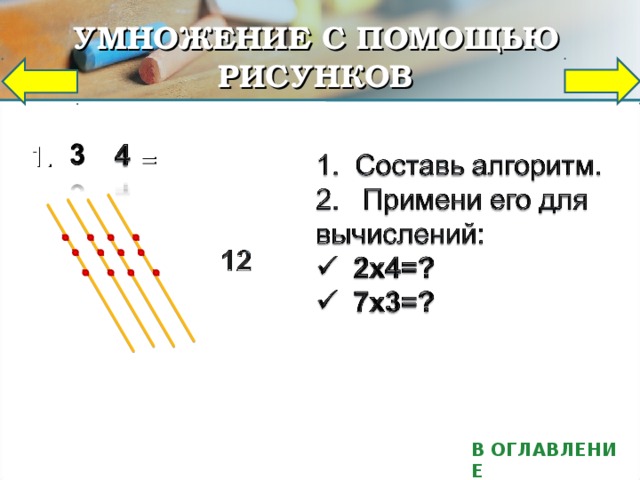
1. Умножение с помощью рисунков.

Учитель предлагает выполнить умножение 3 ∙4 без таблиц умножения.

Ответы учеников: 3∙4 = 3+3+3+3 или 3∙4 = 4+4+4.

Учитель предлагает ученикам построить:

- параллельные прямые, количество, которых совпадает с первым множителем;

- параллельные прямые (количество их равно второму множителю), пересекающие уже построенные прямые;

-посчитать точки пересечения;

- что показывает это число? Построения иллюстрируются с помощью слайда 14.

Учитель просит составить алгоритм умножения и проверить истинность правила ещё на нескольких примерах. ( Примеры на слайде 14).

Дети: « Это правило можно применять только к однозначным числам»?

Методические рекомендации для учителя: дальнейшая работа продолжается в исследовательской и проблемно - поисковой форме. Решение каждого следующего задания отличается от предыдущего дополнительным «шагом» в решении, что заставляет кружковцев, каждый раз, продолжать исследовательскую работу. Учитель помогает ученикам проявить наблюдательность, любознательность и инициативу в познавательной деятельности.

Задание 2: выполнить умножение с помощью рисунков двузначного числа на однозначное: 31х 2.

Дети, работая в парах, делают рисунки.

Учитель просит их:

- составить алгоритм;

-сравнить с предыдущим правилом.

Представители от пар выступают со своими предложениями. Иллюстрация к выступлениям ─ слайд 15.

Ученики выполняют самостоятельно умножение (см. слайд 15), с проверкой.

Задание 3: выполнить умножение с помощью рисунков двузначного числа на двузначное: 12 х 23.

Школьники приступают к выполнению заданий. Им предстоит догадаться о способе вычисления средней цифры в произведении.

Учитель:

- проверяет рисунки, консультирует, при необходимости подсказывает;

-просит определить дополнительный «шаг» в алгоритме;

-после выступления представителя одной из пар, просит составить алгоритм.

Иллюстрация: слайд 16.

Для закрепления выполняются задания (см. слайд 16) с проверкой.

Задание 4: выполнить умножение с помощью рисунков двузначного числа на двузначное: 23 х 14.

Это задание все дети воспринимают как совершенно типичное предыдущему, поэтому:

- одни приступают к его выполнению радостно, вдохновенно;

- другие ─ снисходительно, не очень охотно, так как они не любят чисто механические операции.

После подсчёта точек пересечения прямых («узелков») они получают двузначные числа, чего в предыдущих заданиях не встречалось.

Проблема для кружковцев: как изменить правило для таких чисел?

Учитель:

- руководит дискуссией;

- просит определить дополнительный «шаг» в алгоритме;

- выслушивает предложения, консультирует.

Иллюстрация к выступлениям ─ слайд 17.

Выполнятся самостоятельная работа с последующей проверкой.

Задание 5: выполнить умножение с помощью рисунков трёхзначного числа на двузначное: 123 х 21.

После выполнения построения ученики сталкиваются с новой проблемой: на рисунке получилось два прямоугольника, значит, правило надо изменить.

Учитель:

- выслушивает предложения, консультирует;

- просит определить дополнительные «шаги» в алгоритме;

- предлагает составить алгоритм.

Иллюстрация к выступлению ─ слайд 18.

Выполнятся самостоятельная работа с проверкой.

Учитель просит школьников высказаться о целесообразности применения этого способа умножения.

Дети:

- этот способ вычисления очень интересен;

- он, действительно, может помочь тем, кто не знает таблицу умножения, но с «серьёзными» числами его применение не рационально.

1. Умножение без таблиц на 101, 1001….

Учитель предлагает творческие задания кружковцам:

Задание1:

- выполните умножение 36 х101 «столбиком»;

-подумайте, как можно получить это число без умножения «столбиком»?

Сформулируйте правило. Иллюстрация ─ слайд 19.

Задание2: (с выбором ответа и с проверкой):

Учитель просит проявить наблюдательность и, опираясь на результат предыдущего задания и логические умозаключения, выбрать верный ответ.

36∙1001=?

а). 363636; б). 360036; в). 36036.

36 ∙10001=?

а). 36036036; б). 360036; в). 3600036.

Учитель:

-просит сформулировать правило;

- продолжить формулу: ху ∙ 100…01 =? ( ху00…0ху)

n-1

n

1. Умножение без таблиц на 11.

Ученики получают задание 1: выполните умножение: 34∙11 «столбиком» или устно.

Учитель:

- проследите, как расположились цифры 3 и 4 в произведении;

- как можно получить цифру десятков в произведении?

-попробуйте сформулировать правило. Слайд 20:

Выполните самостоятельную работу ( устно) с проверкой.

Ученики получают задание 2: 48∙11 (сумма цифр больше 10).

Часто ученики сами предлагают такое задание и обозначают проблему: «Как изменится правило, если сумма цифр будет больше 10»?

Кружковцы работают в парах: дискутируют, совещаются.

Учитель:

-консультирует, выслушивает предположения;

-просит подумать и попытаться сформулировать правило.

К выступлению ─ слайд 21.

Самостоятельная работа с последующей проверкой позволяет закрепить правило.

4.Учитель предлагает творческое задание:

- на конкретных примерах умножения на 111 проследить за результатами и сформулировать правило умножения на 111, на 1111…

Иллюстрация: слайды 22 и 23

- продолжить равенство: ху∙111…1 =? ( х(х+у)(х+у)…(х+у)у)

n

n-1

4.Учитель просит школьников высказаться о целесообразности применения изученного способа умножения на 101, 1001.. и на 11, 111.. .

100% школьников сделали вывод: эти способы умножения упрощают вычислительные действия, их целесообразно применять.

1. Подведение итогов.

Отметки выставляю только хорошие и отличные в зависимости от набранных баллов каждым кружковцем. Каждый ответ оценивается 1 баллом.

1. Анализ интереса учащихся к теме.

По результатам рефлексии положительную учебную мотивацию имеют 100% учащихся.
Учащимся было предложено выбрать вариант соответствующий их ощущениям после урока.
1. Я все знаю, понял и могу объяснить другим.
2. Я все знаю, понял, но не уверен, что смогу объяснить другому.
3. Я сам знаю, понял, но объяснить другому не смогу.
4. У меня остались некоторые вопросы.
Из предложенных вариантов выбрали:
1. – 84 %;
2. – 10 %;
3. – 4 %;
4. – 2%.

1. В конце занятия выдаётся творческое домашнее задание: пользуясь различными источниками изучить старинные способы умножения на пальцах. Пример: Слайд 25.

Пояснения к презентации

Изложение материала на слайдах 14-24 начинается по щелчку и продолжается автоматически на остальных слайдах начинается и продолжается автоматически. Автоматический режим выбрала с целью активизации произвольного внимания учеников и его концентрации. Об автоматическом режиме переключений предупреждаю заранее, что мобилизует внимание, воспитывает дисциплину, приучает работать в непривычной ситуации. При необходимости темп занятия можно изменить, учитывая недостатки в развитии внимания некоторых учеников.

Переход к следующему слайду осуществляется по щелчку ( слайды 1-4), по клику на значок ( слайды 5- 27) , поэтому есть возможность после просмотра каждого слайда сделать вывод, определить тип задачи и сделать записи в тетрадях алгоритма решения каждой задачи. К предыдущему слайду можно вернуться по значку. Переход к оглавлению ─. Самостоятельные работы проверяются по клику на слово: «Проверь».

Литература и интернет ресурсы

1.     Автайкина А.К. Некоторые формы организации устного счета. Математика в школе, 1991, №3, 21-23с.

2. Депман И.Я. История арифметики.─ Издание 3-е.─М.:Комкнига, 2006.─ 416 с.

3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 классов─М.:Просвещение,1989. ─ 287 с.

4. http://nsportal.ru/ap/nauchno-tekhnicheskoe-tvorchestvo/library/neobychnye-sposoby-umnozheniya

5. http://www.iralebedeva.ru/inform7.html

6. http://temirtau.kuz.ru/teachers/Kazanina/Kazanina1.html

7. http://do.gendocs.ru/docs/index-364762.html

Приложение 1. Раздаточный материал «Решётка»

	3	6	3
2
5
4
1

17

Автор : Будко Любовь Фёдоровна.

Должность: учитель математики.

Предметная область: математика и информатика.

Участники: учащиеся 5-6 классов.

ОГЛАВЛЕНИЕ

В ОГЛАВЛЕНИЕ

«МАЛЫЙ ЗАМОК»

Выполни умножение

по образцу:

Проверь:

В ОГЛАВЛЕНИЕ

6

«РЕВНОСТЬ»

х

=

5

8

1

Результат читается снизу и справа

Сложим числа по диагоналям:

2

3

2

0

4

8

Выполни умножение по образцу:

1452 х 363

2

1

3

0

6

2

1

1

2

Проверь:

0

8

6

1

0

0

В ОГЛАВЛЕНИЕ

РУСКИЙ КРЕСТЬЯНСКИЙ СПОСОБ

Пример 2

Пример 1

Если множимое не делится на два:

Выполни умножение по образцу:

В ОГЛАВЛЕНИЕ

8

ВЫЧИСЛИ ПО ОБРАЗЦУ:

Проверь:

В ОГЛАВЛЕНИЕ

ИНДИЙСКИЙ СПОСОБ

Вычисли по образцу: 342 х 6

Проверь

В ОГЛАВЛЕНИЕ

АРАБСКИЙ СПОСОБ

Вычисли по образцу: 342 х 6

1

Проверь

Ответ:2052

Пояснения

В ОГЛАВЛЕНИЕ

ВОПРОСЫ ГРУППАМ

• Сравните старинные способы умножения с современными:
• Какие преимущества

( недостатки) вы увидели в старинных способах?

• Планируете ли вы какой-то из способов применять на практике?

В ОГЛАВЛЕНИЕ

ДЛЯ ТЕХ, КТО НЕ ЗНАЕТ ТАБЛИЦУ УМНОЖЕНИЯ:

• Умножение с помощью рисунков.
• Умножение чисел на 101,1001,...
• Умножение чисел на 11.
• Умножение чисел на 111, 1111,…

В ОГЛАВЛЕНИЕ

УМНОЖЕНИЕ С ПОМОЩЬЮ РИСУНКОВ

1.

=

В ОГЛАВЛЕНИЕ

Пример 2

=

Проверь:

В ОГЛАВЛЕНИЕ

Пример 3

3

2

=

Составь алгоритм. Реши самостоятельно:

Проверь:

В ОГЛАВЛЕНИЕ

Пример 4

4

1

=

Составь алгоритм.

Реши самостоятельно :

1 . 32х41; 2. 25х14

1

1

В ОГЛАВЛЕНИЕ

Пример 5

1

3

1

3

2

=

2

=

+

+

=

Проверь

В ОГЛАВЛЕНИЕ

Умножение числа на 101 1001…

Сформулируй правило

Проверь:

Умножение числа на 11

Для самостоятельного

решения:

Проверь:

Сформулируй правило

В ОГЛАВЛЕНИЕ

Пример2 умножения числа на 11

Реши самостоятельно :

Проверь

Сформулируй правило

В ОГЛАВЛЕНИЕ

УМНОЖЕНИЕ НА 111

Выполни умножение:

Проверь:

=

Сформулируй правило

В ОГЛАВЛЕНИЕ

Пример 2

Реши самостоятельно :

Проверь:

13

13

=

=

=

3+1

=

Сформулируй правило

В ОГЛАВЛЕНИЕ

Умножения на 9 на пальцах

Положите свои руки на стол и мысленно пронумеруйте пальцы слева направо от 1 до 10. Выполним действие умножения, допустим 9 х 3. Загибаем третий слева палец. Оставшиеся не загнутыми пальцы слева образуют количество десятков (2) , а не загнутые справа — количество единиц (7). Ответ: 27.

Потренируйтесь в парах:

1. 9х6 =?; 2. 9х7=?...

В ОГЛАВЛЕНИЕ

ДОМАШНЕЕ ЗАДАНИЕ

Изучить старинные способы умножения на пальцах

В ОГЛАВЛЕНИЕ