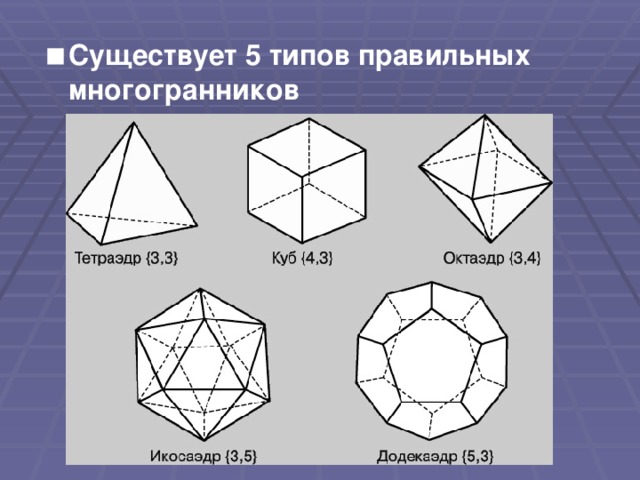
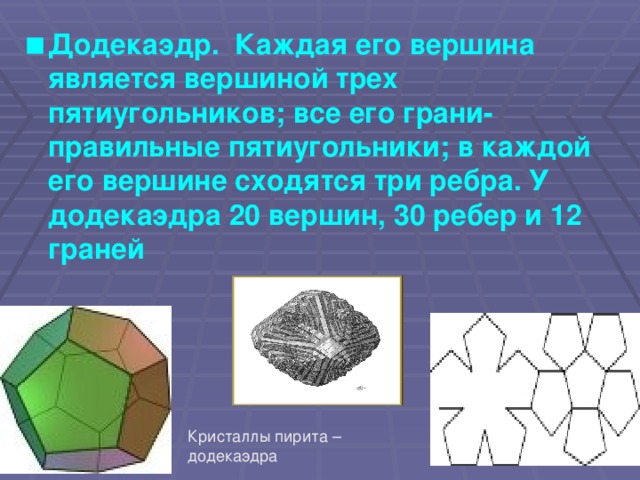
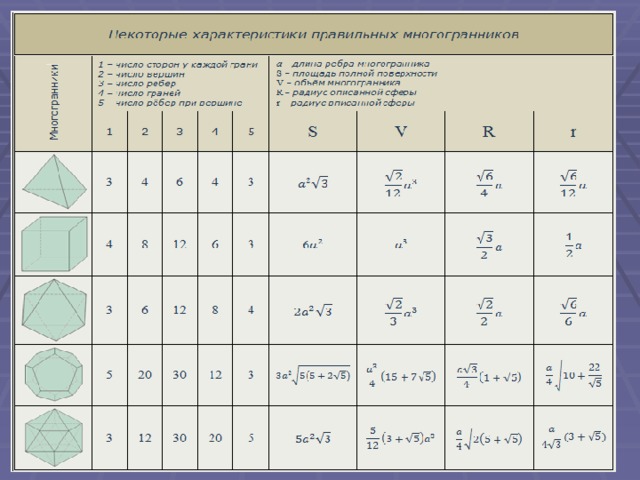
Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.
?Грани многогранника - это многоугольники, которые его образуют.
?Ребра многогранника - это стороны многоугольников.
?Вершины многогранника - это вершины многоугольника.
?Диагональ многогранника - это отрезок, соединяющий 2 вершины, не принадлежащие одной грани.