МНОГОГРАННИКИ
Выпуклые многогранники. Теорема Эйлера
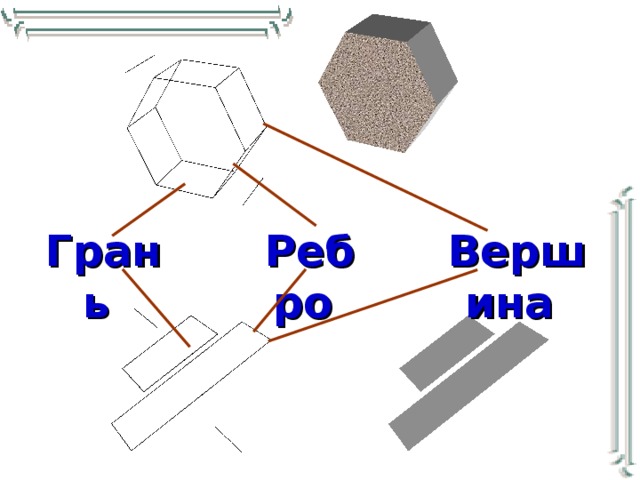
В школьных учебниках геометрии многогранниками обычно называются тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.
Многогранник называется выпуклым, если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок.
На рисунке 1 приведены примеры выпуклых и невыпуклых многогранников.
Рассмотрим некоторые свойства выпуклых многогранников.
Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
Доказательство. Пусть F - какая-нибудь грань многогранника M, и A, B – точки, принадлежащие грани F (рис. 2). Из условия выпуклости многогранника M, следует, что отрезок AB целиком содержится в многограннике M. Поскольку этот отрезок лежит в плоскости многоугольника F, он будет целиком содержаться и в этом многоугольнике, т.е. F - выпуклый многоугольник.
Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.
Доказательство. Пусть M - выпуклый многогранник. Возьмем какую-нибудь внутреннюю точку S многогранника M, т.е. такую его точку,