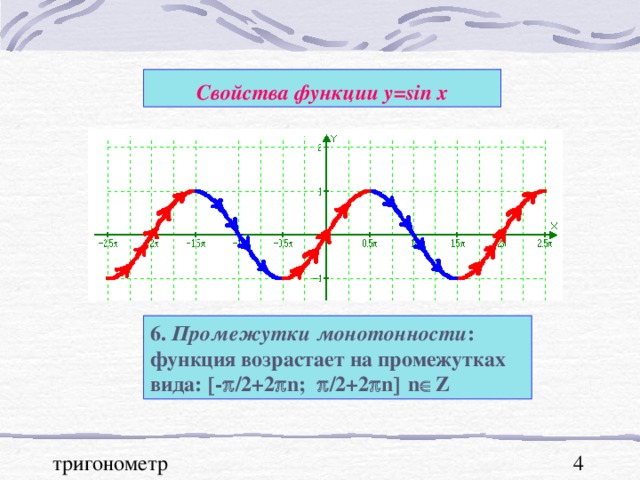
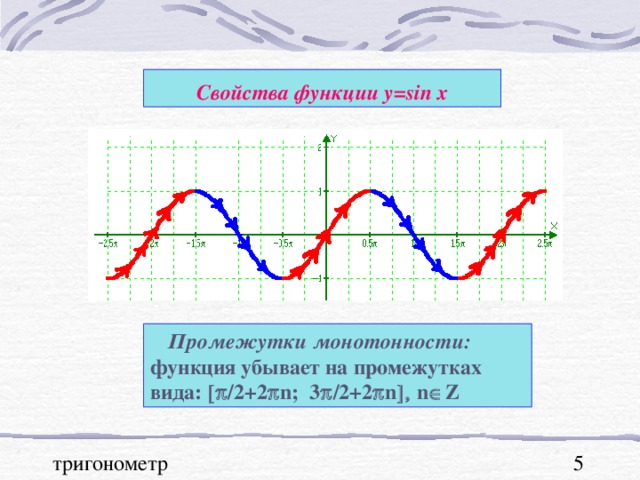
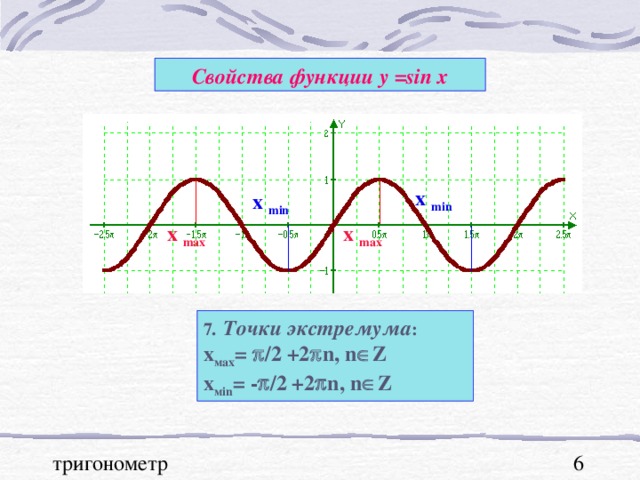
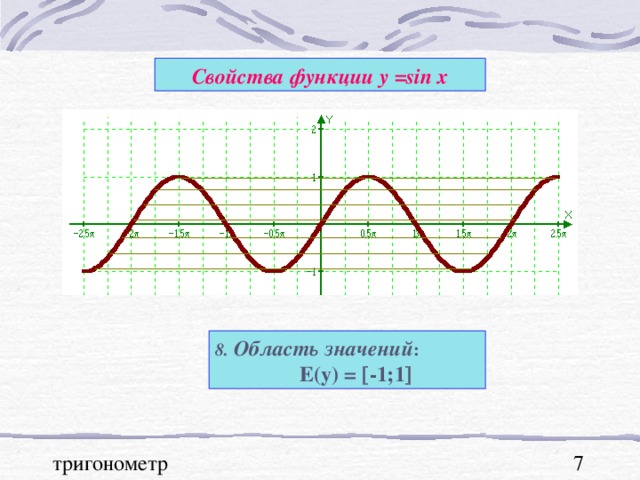
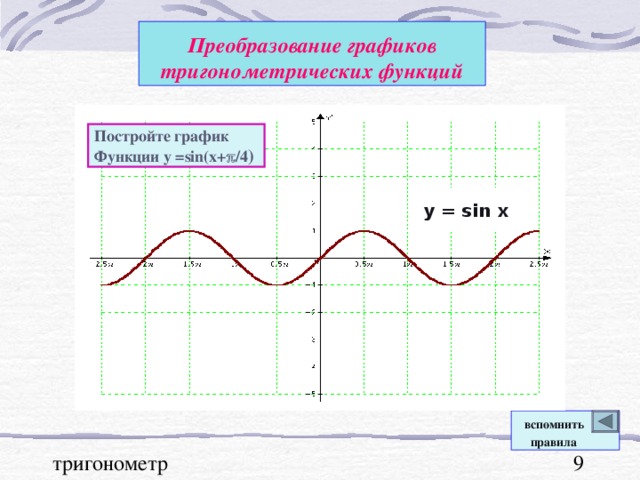
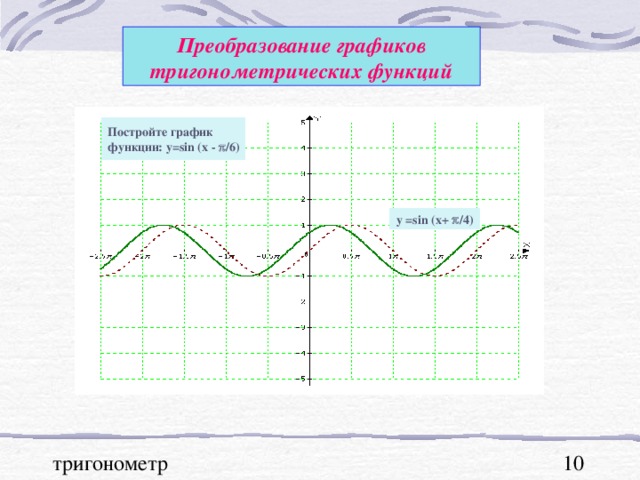
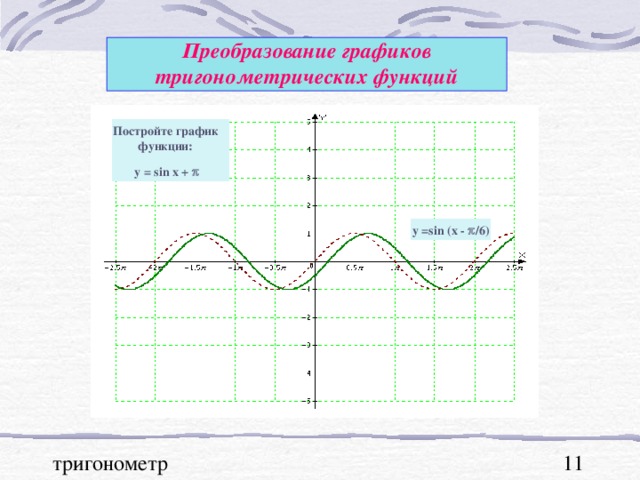
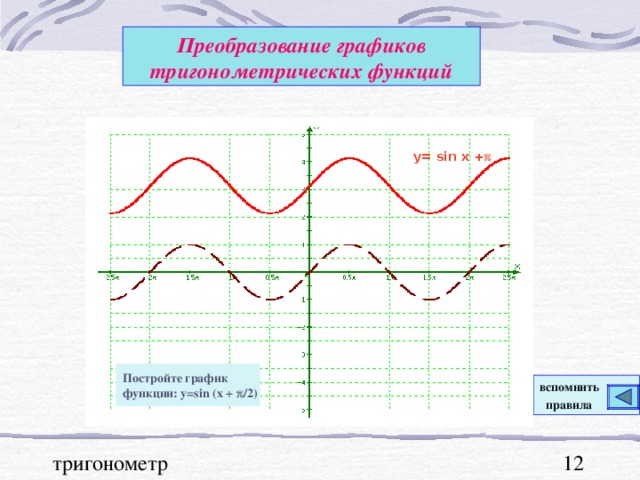
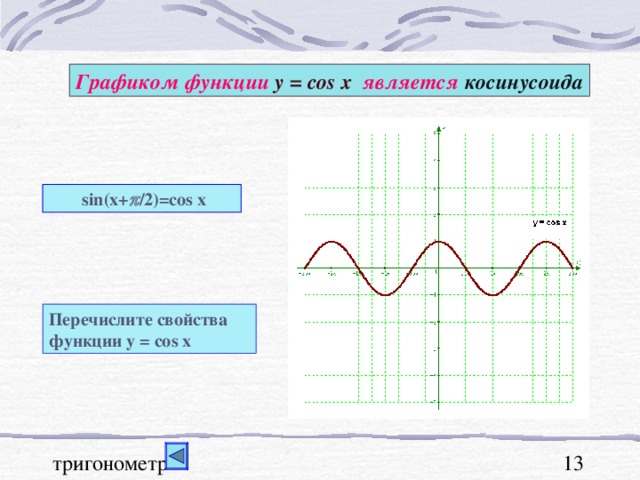
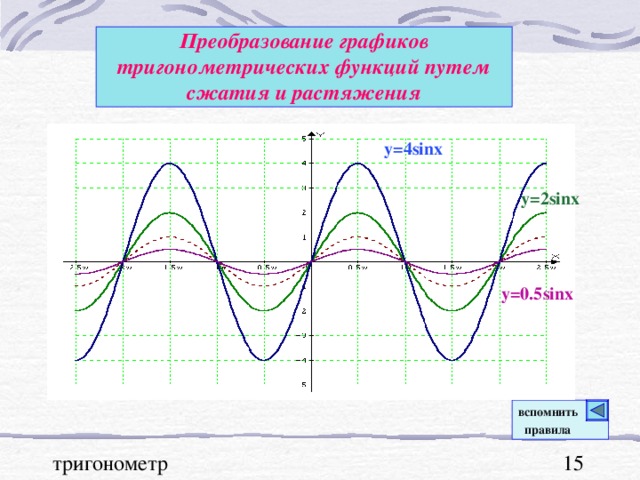
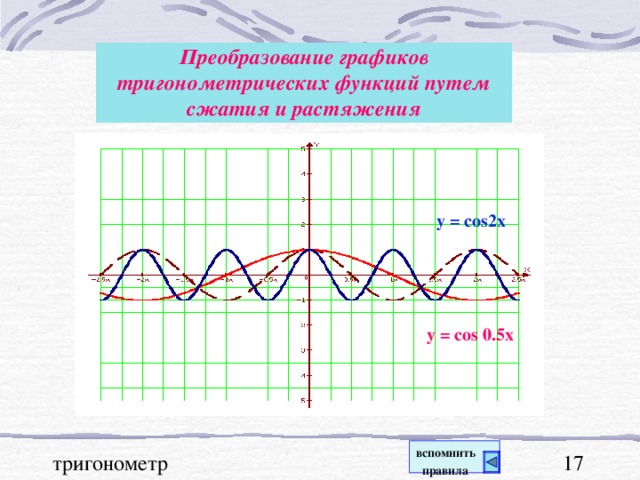
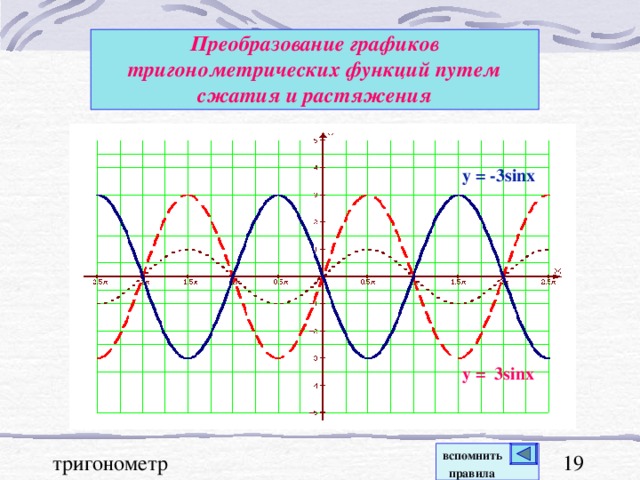
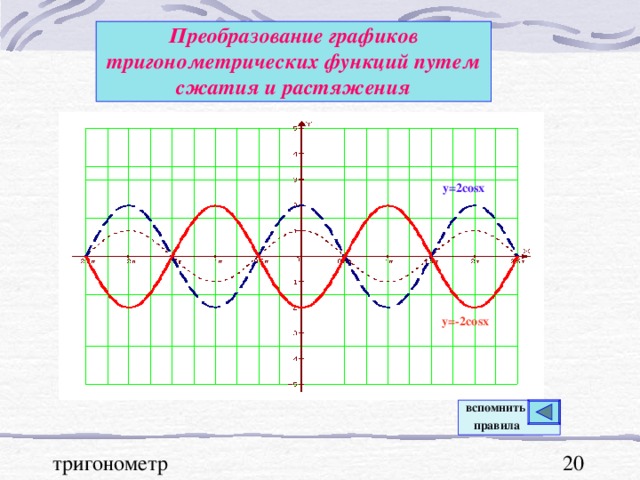
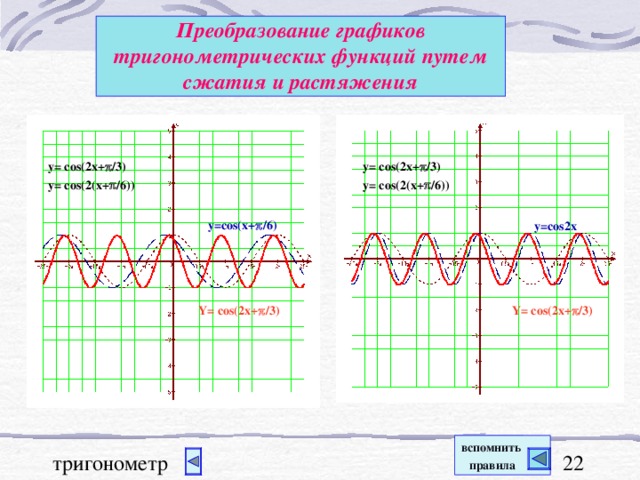
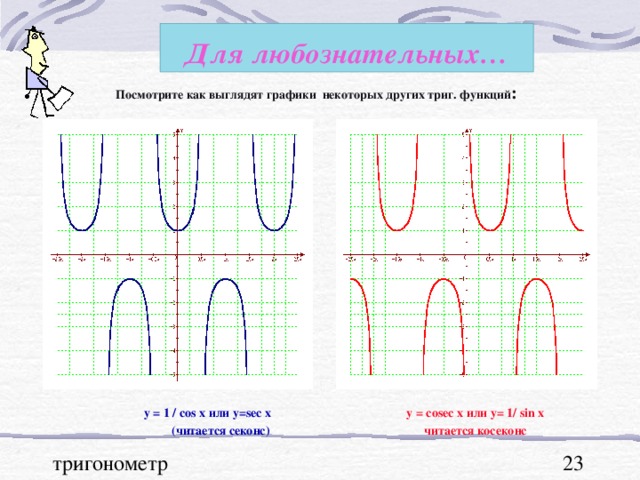
В презентации "Графики тригонометрических функций, преобразование графиков" подробно рассмотрены свойства функции y=sinx. На примерах графиков функций y=sinx и y=cosx рассмотрены преобразования графиков: параллельный перенос вдоль оси ОХ и вдоль оси ОУ; растяжение и сжатие графиков вдоль координатных осей. Для любознательных показаны графики функций y=secx и cosecx и указаны ссылки на интернет ресурсы о тригонометрических функциях.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Графики тригонометрических функций, преобразование графиков.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Графики тригонометрических функций, преобразование графиков. »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1340 руб.
2240 руб.
1900 руб.
3170 руб.
1730 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

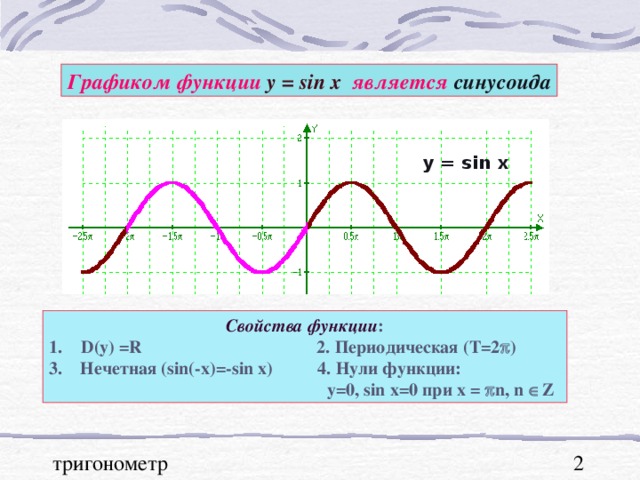
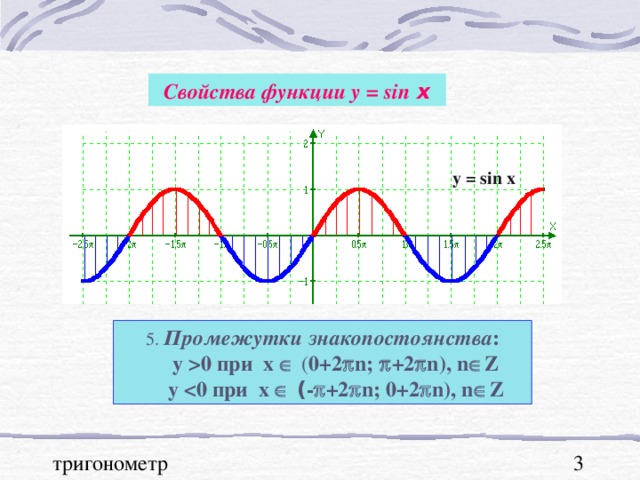 0 при х ( 0+2 n ; +2 n ) , n Z у при x ( - +2 n ; 0+2 n), n Z" width="640"
0 при х ( 0+2 n ; +2 n ) , n Z у при x ( - +2 n ; 0+2 n), n Z" width="640"