Цель урока: закрепить, привести в систему и углубить знания и умения по теме: «Преобразование графиков тригонометрических функций y=sinx и y=cosx”;
Задачи: -образовательные: сформировать и закрепить умения и навыки построения графиков тригонометрических функций y=sinx и y=cosx, используя различные преобразования; закрепить знания свойств данных функций; способствовать самостоятельной деятельности учащихся;
- развивающая: развивать логическое мышление, внимательность, аккуратность, расширять кругозор, развивать познавательный интерес к предмету;
- воспитательная: воспитывать терпение, усидчивость, упорство в достижении поставленных целей, формировать ответственность перед коллективом, организованность, дисциплинированность, чувство долга,инициативу и творчество в учебном процессе.
Тип урока: обобщающий.
Форма урока: урок-обобщение, контрольно-проверяющий.
Методы обучения: объяснительно-иллюстративный, частично-поисковый с элементами самостоятельной работы, метод информационных технологий.
Методические приемы: личностно-ориентированное, проблемное и развивающее обучение.
Оборудование: мультимедийная аппаратура, презентация, раздаточный материал, справочный материал.
Ход урока.
- Организационный момент
II.Актуализация опорных знаний.
1. Проверка домашнего задания
Перечислите этапы построения графиков функций
№1(а) y= 2sin(x-п/3)
№1(б) y= -3cos(x+п/6)
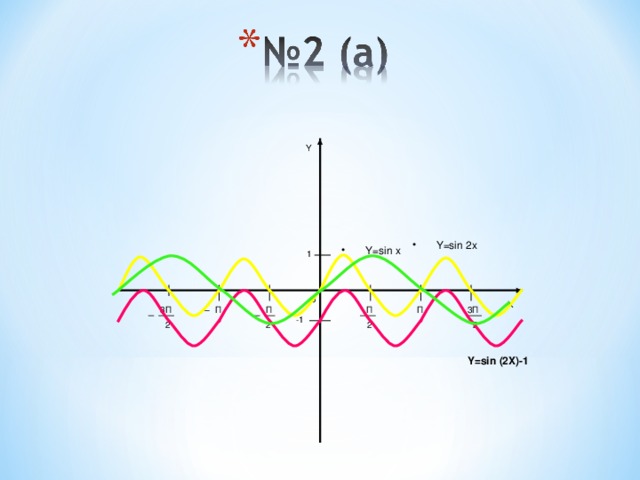
№2(а) y= sin2x-1
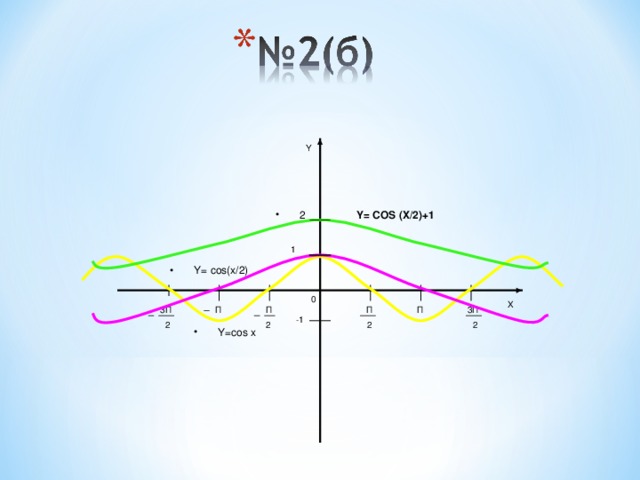
№2(б) y= cos(x/2)+1
2. Устная работа.
1) Теоретический опрос: перечислите преобразования, которые используются для построения графиков функций
2) Для данных графиков функций, изображенных на рисунках, выберите аналитическую запись.
III. Практическая работа.
Постройте график функции и устно прочитайте его
IV.Самостоятельная работа на карточках по двум вариантам.
V. Это интересно. Рассмотрим примеры использования тригонометрических функций при описании и изучении различных жизненных процессов
VI.Итоги урока
VII. Домашнее задание.
Просмотр содержимого документа
«Самостоятельная работа В.1»
Просмотр содержимого документа
«Самостоятельная работа В.2»
Просмотр содержимого документа
«Тест Свойства и графики тригонометрических функци В.1»
Свойства и графики тригонометрических функций.
Тест
Вариант-1
1)Найдите область значений функции y= 2- 3sin x
а) [-1;5] б) [-4;2] в)[-5;1] г)[-2;4]
2)Найдите нули функции y=1/3 cos 2x на промежутке [-П/2;2П] и запишите их сумму:
а)1,5П б) 2П в)3,75П г)2,25П
3)Для функции y= sin (x/2 – П/6) найдите точку минимума на промежутке [0; 4П]
а) 7П/2 б) 7П/ в)10П/3 г)5П/3
4)Найдите промежутки убывания функции y=cos (П/3 +2/3*X)
а)[-П/2+2/3*Пn; П/2+2/3*Пn] в)[П/2+3Пn;2П+3Пn]
б)[- П/2+3Пn; П+3Пn] г)[-П/6+2/3*Пn;2П/3+2/3*Пn]
5)Расположите в порядке возрастания числа sin 1,sin(-5),cos1
а) sin(-5), sin 1, cos1 в) sin(-5), cos1, sin 1
б) sin 1, sin(-5), cos1 г) cos1, sin 1, sin(-5)
6) По графику некоторой функции запишите формулу, которой она задана.
а) y= sin (2x-П/3);
б) y= sin (2x+2П/3);
в) y= sin (x+П/3);
г) y= sin (x/2-П/3);

7)Исследовать и построить график функции
y= 2cos x/2
y=1/2 sin (x/2-П/6)
Просмотр содержимого документа
«Тест Свойства и графики тригонометрических функций В.2»
Свойства и графики тригонометрических функций.
Тест
Вариант-2
1)Найдите область значений функции y=3-5 cos x.
а)[-2;2] ; б)[-3;5] ; в) [-5;3] ; г) [-2;8].
2
)Найдите нули функции y=0,5 sin 3x на промежутке [-П;П/2 ] и запишите их сумму.
а) 5П б) _ 5П в) 4П г)_ 8П




 6 6 3 3
6 6 3 3
 3) Для функции y = cos ( x/3 +П/4) найдите точку минимума на промежутке [0;6П].
3) Для функции y = cos ( x/3 +П/4) найдите точку минимума на промежутке [0;6П].
а) 3,75П б) 4,5П в) 3,25П г) 5,25П
4)Найдите промежутки возрастания для функции y=sin (П/6 + X/3).
а) [-П +2П/3 n; 2П +2П/3 n ] в) [-2П + 6Пn; П+6 Пn]
б) [-П/3 + 2Пn/3; П/2 + 2Пn/3] г) [-П/2 +6Пn;2П+6Пn]
5)Расположите в порядке убывания числа cos2 ,cos(-4),sin2.
а) cos(-4), sin2,cos2 б) cos2 , sin2, cos(-4)
в) sin2, cos2 , cos(-4) г) cos(-4), cos2 , sin2
6)По графику некоторой функции запишите формулу, которой она задана.
a) y= cos (2x- П/3)
б) y= cos (2x+ П/6)
в) y= cos (2x – П/6)
г) y= cos (x/2+ П/6) 
7)Исследовать и построить график функции
y=1/2 sin 2x
y=3cos (3x-3П/4)
Просмотр содержимого презентации
«готовый вариант презентации»

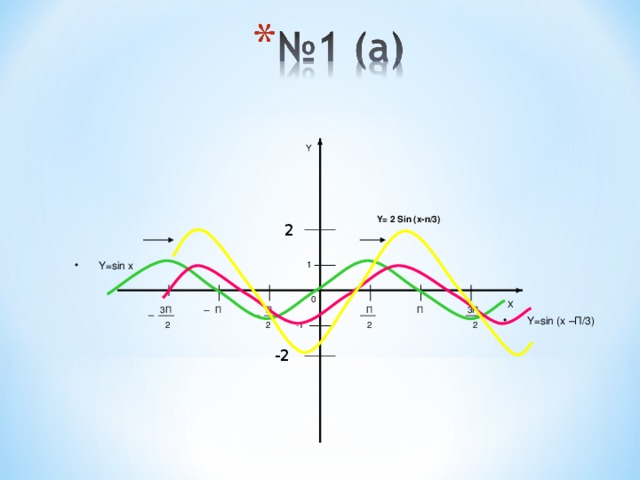
Y
Y= 2 Sin (x-п/3)
2
1
0
X
П
П
П
3П
П
3П
2
2
2
2
-1
-2
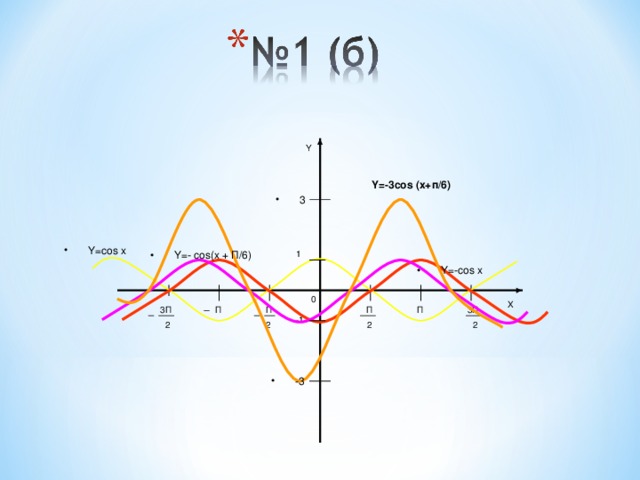
Y
Y=-3cos (x+п/6)
1
0
X
П
П
3П
3П
П
П
-1
2
2
2
2
Y
1
0
X
3П
3П
П
П
П
П
-1
2
2
2
2
Y=sin (2X)-1
Y
Y= COS (X/2)+1
1
0
X
П
3П
3П
П
П
П
-1
2
2
2
2
 0 f (x) 0 x График функции y=f (x) + a получается из графика функции y=f (x) параллельным переносом вдоль оси ординат на a единиц вверх , если a0." width="640"
0 f (x) 0 x График функции y=f (x) + a получается из графика функции y=f (x) параллельным переносом вдоль оси ординат на a единиц вверх , если a0." width="640"
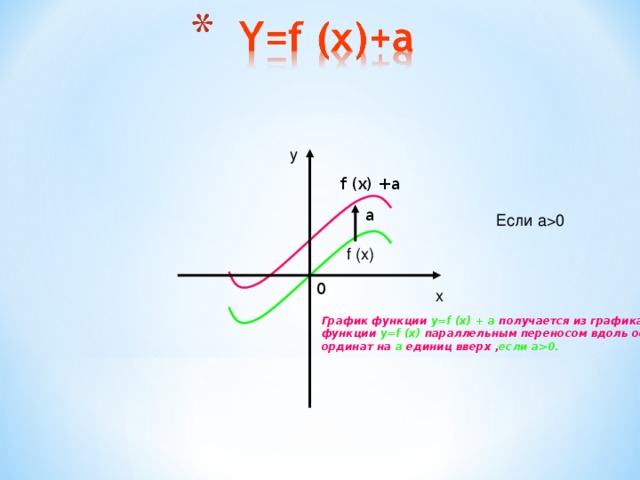
y
f (x) +a
a
Если a0
f (x)
0
x
График функции y=f (x) + a получается из графика
функции y=f (x) параллельным переносом вдоль оси
ординат на a единиц вверх , если a0.
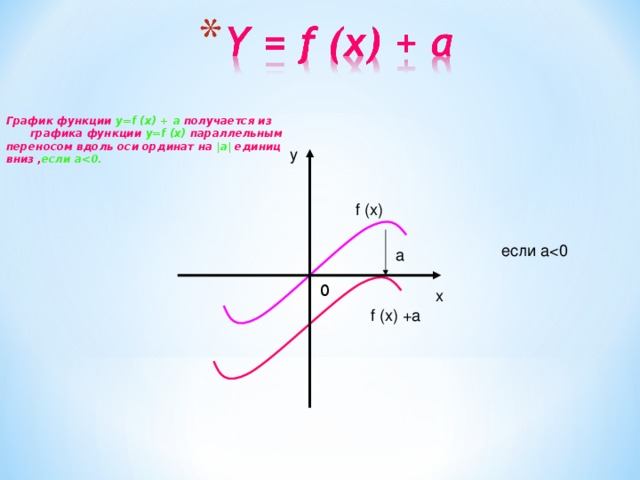
График функции y=f (x) + a получается из графика функции y=f (x) параллельным
переносом вдоль оси ординат на |a| единиц
вниз , если a
y
f (x)
если a
a
0
x
f (x) +a
 0 a f (x-a) 0 x График функции y= f (x-a) получается из графика функции y=f (x) параллельным переносом вдоль оси абсцисс на а единиц вправо, если а 0." width="640"
0 a f (x-a) 0 x График функции y= f (x-a) получается из графика функции y=f (x) параллельным переносом вдоль оси абсцисс на а единиц вправо, если а 0." width="640"
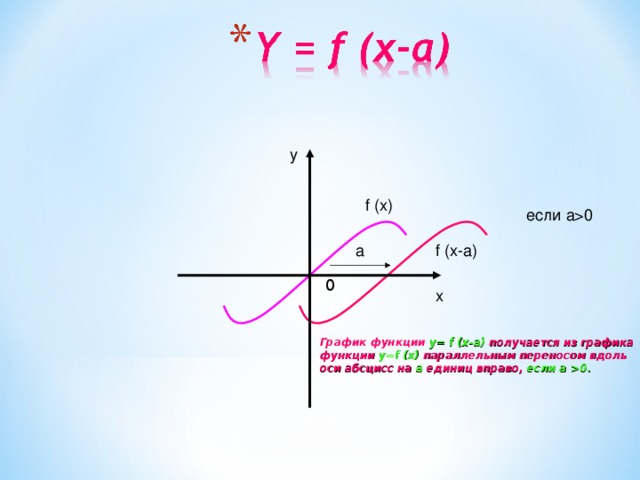
y
f (x)
если a0
a
f (x-a)
0
x
График функции y= f (x-a) получается из графика
функции y=f (x) параллельным переносом вдоль
оси абсцисс на а единиц вправо, если а 0.
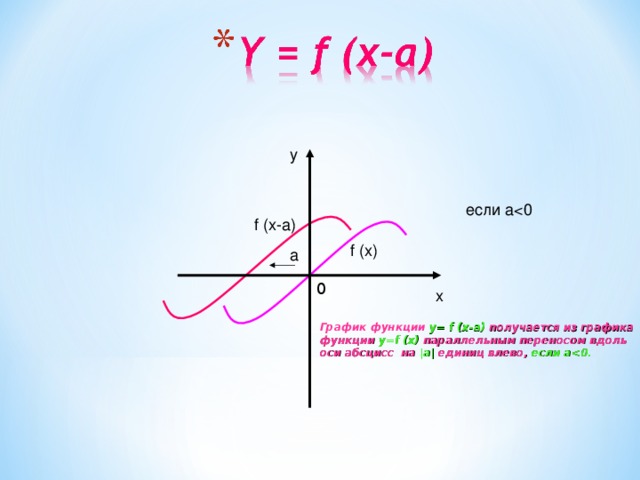
y
если a
f (x-a)
f (x)
a
0
x
График функции y= f (x-a) получается из графика
функции y=f (x) параллельным переносом вдоль
оси абсцисс на |а| единиц влево, если a
 1 f (x) 0 x График функции y=k f (x) получается из графика функции y=f (x) путем его растяжения в k раз при k1 от оси абсцисс." width="640"
1 f (x) 0 x График функции y=k f (x) получается из графика функции y=f (x) путем его растяжения в k раз при k1 от оси абсцисс." width="640"
y
k f (x)
k1
f (x)
0
x
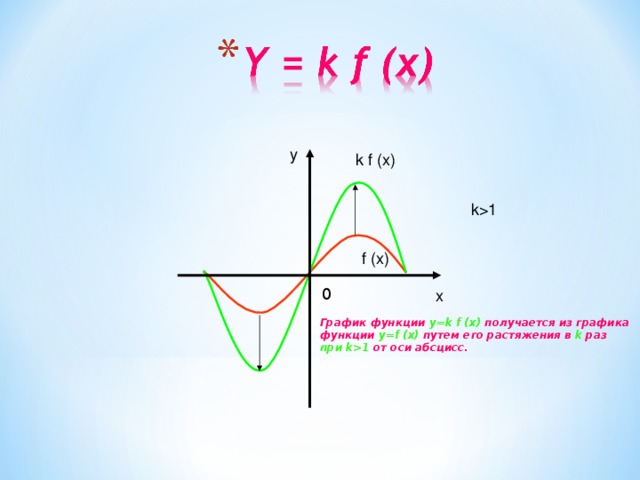
График функции y=k f (x) получается из графика
функции y=f (x) путем его растяжения в k раз
при k1 от оси абсцисс.
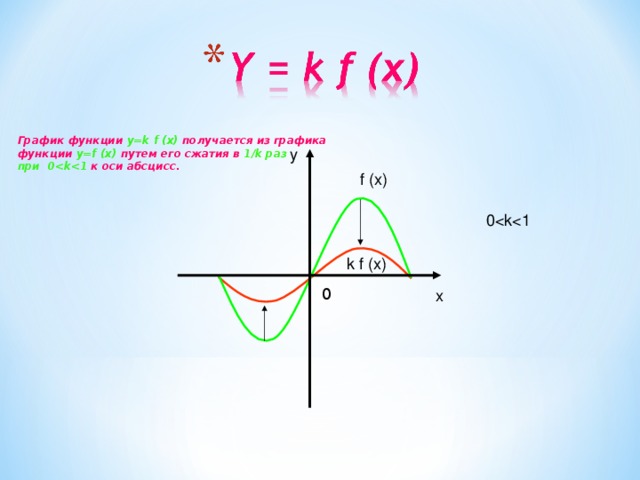
График функции y=k f (x) получается из графика
функции y=f (x) путем его сжатия в 1/k раз
при 0 к оси абсцисс.
y
f (x)
0
k f (x)
0
x
 1 f (x) 0 x График функции y= f (k x) получается из графика функции y=f (x) путем его сжатия в k раз при k1 к оси ординат." width="640"
1 f (x) 0 x График функции y= f (k x) получается из графика функции y=f (x) путем его сжатия в k раз при k1 к оси ординат." width="640"
y
f (k x)
k1
f (x)
0
x
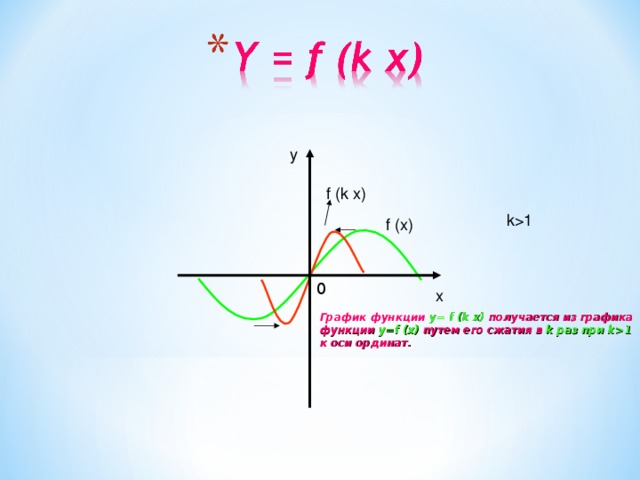
График функции y= f (k x) получается из графика
функции y=f (x) путем его сжатия в k раз при k1
к оси ординат.
y
0
f (x)
f (k x)
0
x
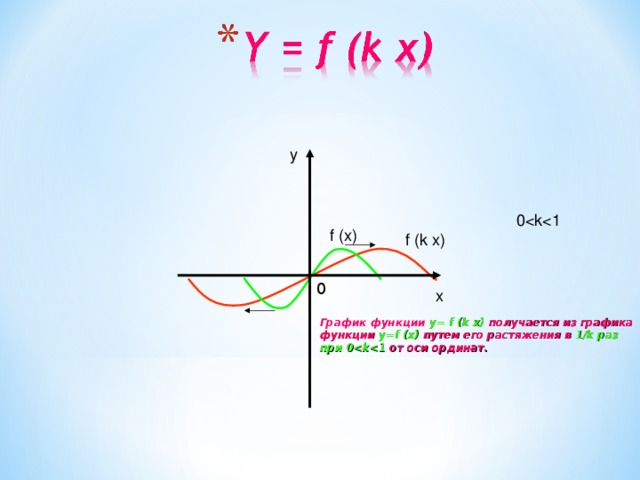
График функции y= f (k x) получается из графика
функции y=f (x) путем его растяжения в 1/k раз
при 0 от оси ординат.
y
f (x)
0
x
-f (x)
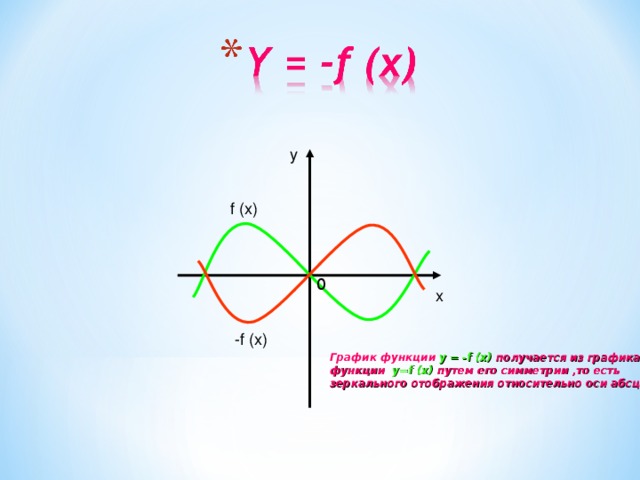
График функции y = -f (x) получается из графика
функции y=f (x) путем его симметрии ,то есть
зеркального отображения относительно оси абсцисс.

Y
- А) y= -2 sinx
- Б)y= cos x/2
- В)y= 1,5 sinx
- Г)y= сos 2x
- Д)y= - 3cosx
- Е)y= sin x/3
- Ж)y= -1,5 cosx
- З)y= sin 3x
1)
0
X
3П
П
П
3П
П
П
2
2
2
2
2)
Y
2
1
0
X
П
П
3П
П
П
3П
-1
2
2
2
2
-2
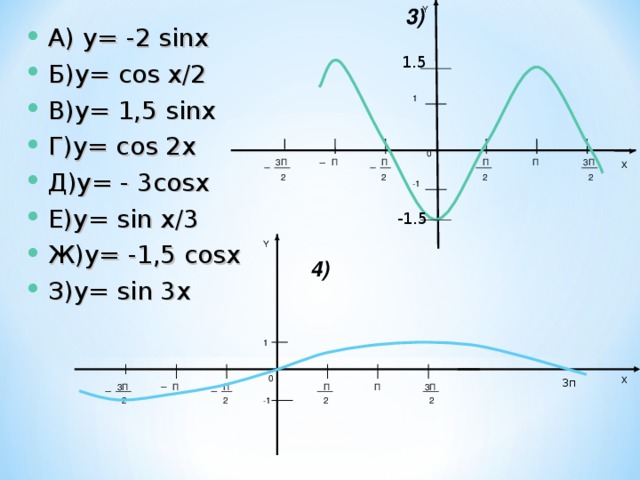
3)
Y
- А) y= -2 sinx
- Б)y= cos x/2
- В)y= 1,5 sinx
- Г)y= сos 2x
- Д)y= - 3cosx
- Е)y= sin x/3
- Ж)y= -1,5 cosx
- З)y= sin 3x
1.5
1
0
П
П
П
3П
П
3П
X
2
2
2
2
-1
-1.5
Y
4)
1
0
X
3п
3П
П
3П
П
П
П
2
2
2
2
-1
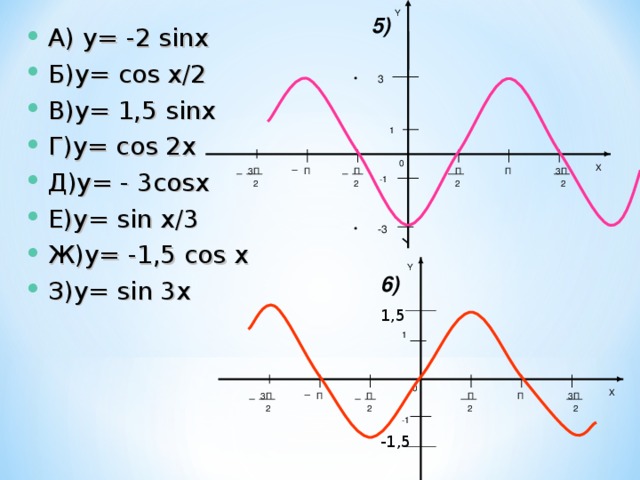
Y
5)
- А) y= -2 sinx
- Б)y= cos x/2
- В)y= 1,5 sinx
- Г)y= сos 2x
- Д)y= - 3cosx
- Е)y= sin x/3
- Ж)y= -1,5 cos x
- З)y= sin 3x
1
0
X
3П
3П
П
П
П
П
-1
2
2
2
2
Y
6)
1,5
1
0
X
П
П
П
П
3П
3П
2
2
2
2
-1
-1,5
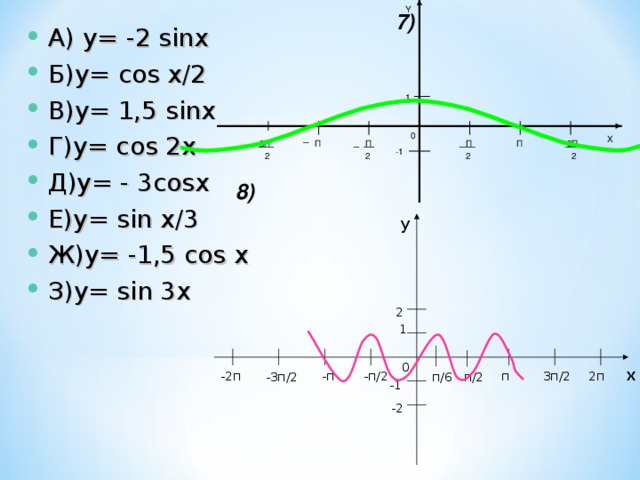
Y
7)
- А) y= -2 sinx
- Б)y= cos x/2
- В)y= 1,5 sinx
- Г)y= сos 2x
- Д)y= - 3cosx
- Е)y= sin x/3
- Ж)y= -1,5 cos x
- З)y= sin 3x
1
0
X
П
3П
П
П
3П
П
-1
2
2
2
2
8)
y
2
1
0
х
3п/2
-п/2
-п
-2п
2п
п
-3п/2
п/2
п/6
-1
-2
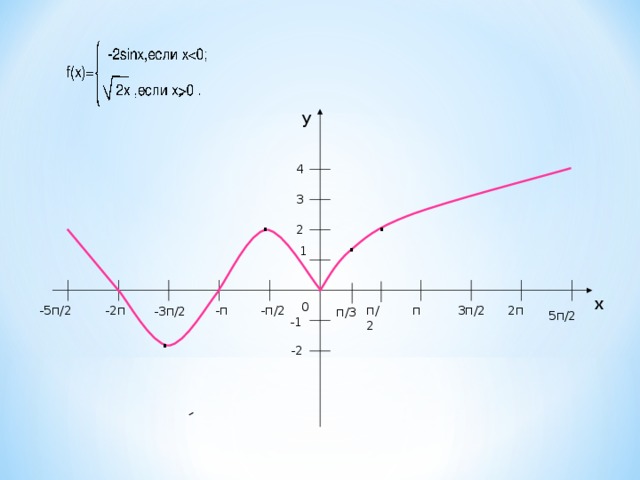
y
4
3
.
.
2
.
1
х
0
-п
3п/2
2п
п
п/2
-5п/2
-2п
-п/2
-3п/2
п/3
5п/2
-1
.
-2

Восход и заход Солнца, изменение фаз Луны, чередование времен года, затмение и движение Планет, биение сердца, вращение колеса, морские приливы и отливы, эпидемии Гриппа .
Все эти процессы периодичны, состояния участвующих в них объектов повторяются.
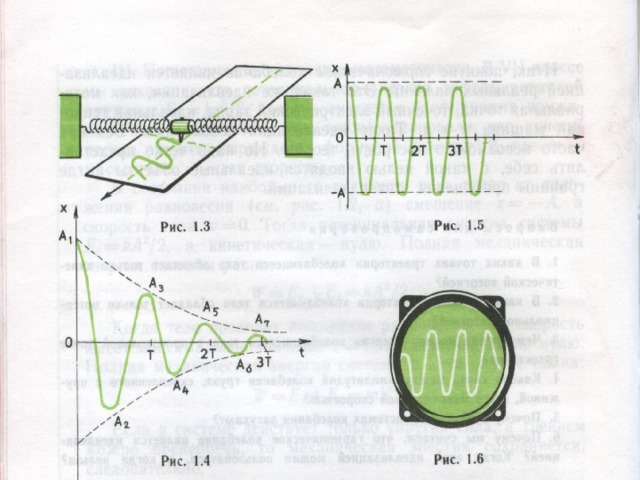






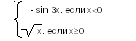


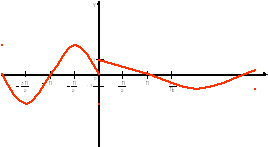
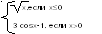
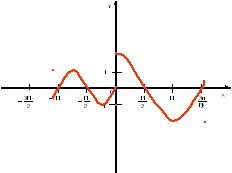




 3) Для функции
3) Для функции 





 0 f (x) 0 x График функции y=f (x) + a получается из графика функции y=f (x) параллельным переносом вдоль оси ординат на a единиц вверх , если a0." width="640"
0 f (x) 0 x График функции y=f (x) + a получается из графика функции y=f (x) параллельным переносом вдоль оси ординат на a единиц вверх , если a0." width="640"

 0 a f (x-a) 0 x График функции y= f (x-a) получается из графика функции y=f (x) параллельным переносом вдоль оси абсцисс на а единиц вправо, если а 0." width="640"
0 a f (x-a) 0 x График функции y= f (x-a) получается из графика функции y=f (x) параллельным переносом вдоль оси абсцисс на а единиц вправо, если а 0." width="640"

 1 f (x) 0 x График функции y=k f (x) получается из графика функции y=f (x) путем его растяжения в k раз при k1 от оси абсцисс." width="640"
1 f (x) 0 x График функции y=k f (x) получается из графика функции y=f (x) путем его растяжения в k раз при k1 от оси абсцисс." width="640"

 1 f (x) 0 x График функции y= f (k x) получается из графика функции y=f (x) путем его сжатия в k раз при k1 к оси ординат." width="640"
1 f (x) 0 x График функции y= f (k x) получается из графика функции y=f (x) путем его сжатия в k раз при k1 к оси ординат." width="640"































