Тип урока. Урок применения новых знаний и умений.
Элементы содержания. Обыкновенные дроби. Изображение обыкновенных дробей на координатном луче. Решение текстовых задач.
Предметные результаты: уметь изображать обыкновенные дроби на координатном луче; решать простейшие текстовые задачи на вычисление значения заданной части величины.
Цели:
научиться определять числитель и знаменатель дроби, что показывает числитель и знаменатель дроби;
понимать, что такое доля, половина, треть и четверть;
уметь записывать и понимать дроби;
научиться решать задачи по нахождению части от числа.
Оборудование: компьютер, проектор.
Ход урока.
I. Введение.
Учитель: Самый первый вопрос, который изучается в курсе математики 5 класса - это натуральные числа. Ребята! Помогите мне! Скажите, какие числа называются натуральными? А ведь с древних времен людям приходилось не только считать предметы (для чего требовались натуральные числа), но и измерять длину, время, площадь, вести расчеты за купленные товары. Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Приходилось учитывать и части, доли меры. Так появились дроби.
В русском языке слово «дробь» появилось в VIII веке, оно происходит от глагола «дробить» - разбивать, ломать на части.
Ребята! Подумайте и отгадайте тему сегодняшнего урока!
(Тема урока: «Доли. Обыкновенные дроби»).
В первых учебниках математики (в XVII веке) дроби так и назывались - «ломаные числа» Современное обозначение дробей берет свое начало в Древней Индии. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает “попасть в трудное положение”.
Но сегодня мы с вами на уроке докажем, что дроби не смогут нас поставить в трудное положение. Вы согласны со мной?
II. Сообщение темы урока (актуализация).
Много с числами хлопот,
Уж такой они народ.
Ну а если встанут в ряд,
То с тобой заговорят.
Ты внимательно смотри
И эти дроби все прочти.
;
Ученики читают дроби.
Объясните, как вы понимаете каждую дробь. Назовите числитель и знаменатель. Какая дробь отличается от остальных? Как вы ее понимаете. (означает целое).Целое в математике обозначается единицей.
Придумайте дробь, которая обозначает целое.
Записываем предложенные дроби на доске и в тетради.
Просмотр слайдов 1,2,3,4,5.
III. Работа в тетради. Задание 1.
Арифметический диктант.
- Запишите дроби ;
- Запишите дробь, у которой числитель5, а знаменатель 9.
- Запишите дробь, у которой знаменатель3, а числитель1.
- Какую дробь называют четвертью, запишите ее.
- Запишите дробь, у которой числитель1, а знаменатель в 7 раз больше.
- Запишите дробь, у которой числитель2, а знаменатель на 3 больше.
Проверка: . (сверившись с соседом - кто-то доски )
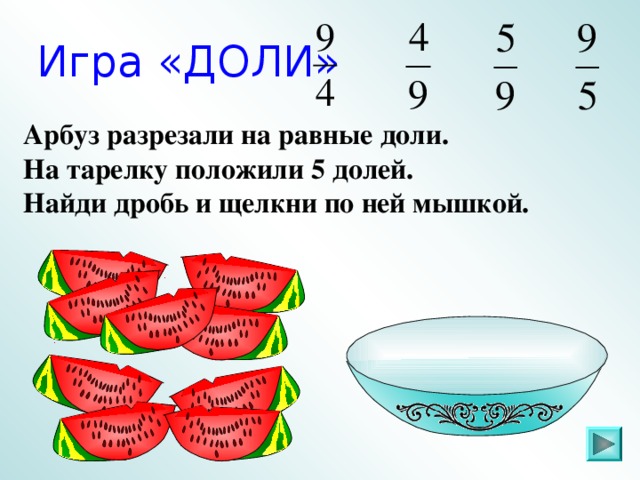
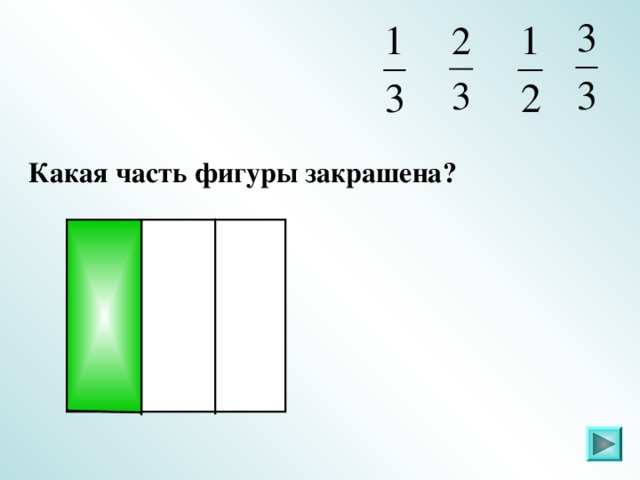
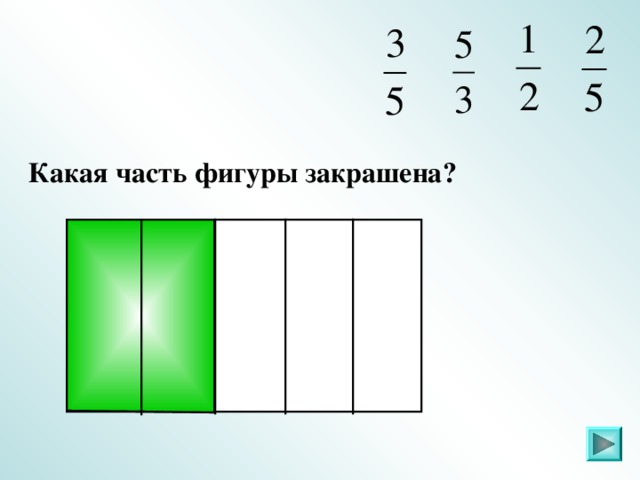
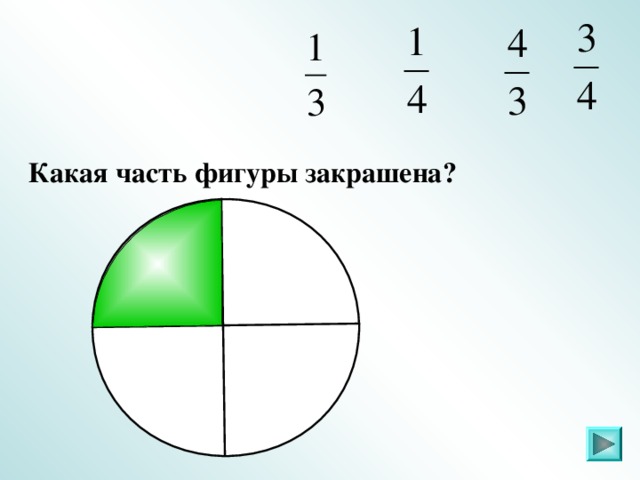
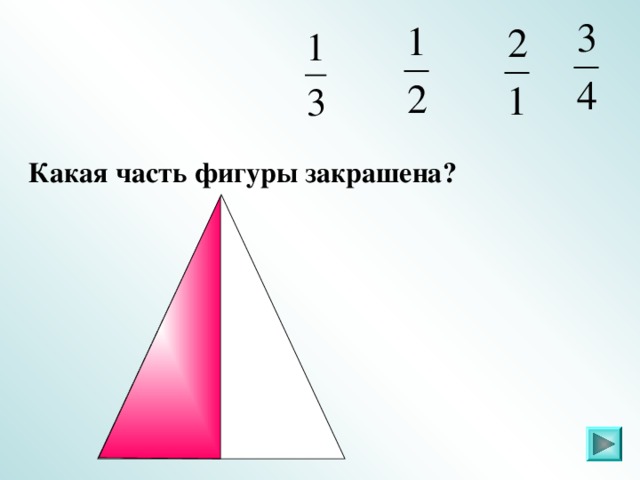
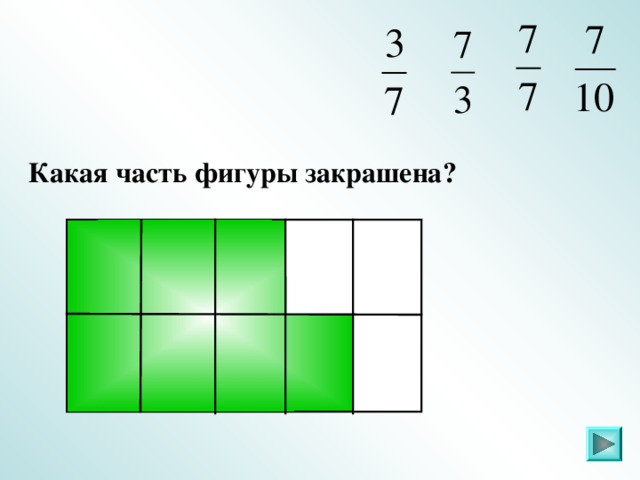
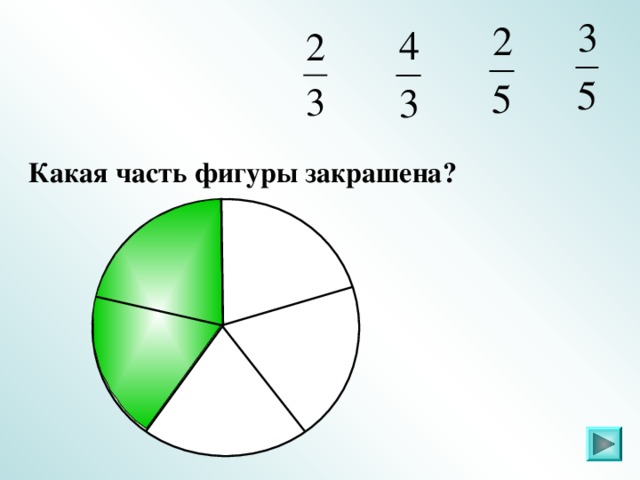
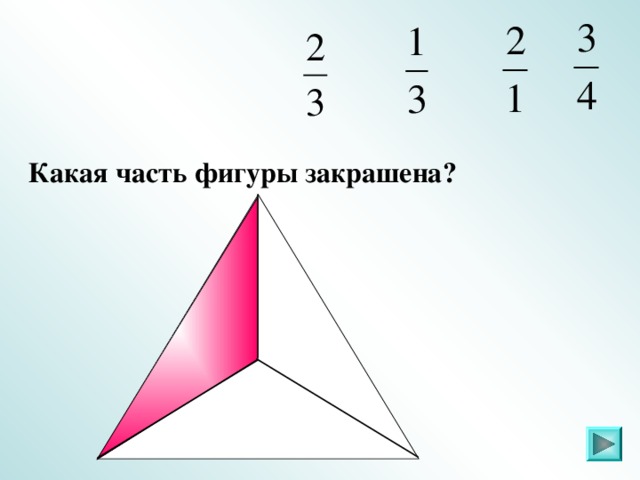
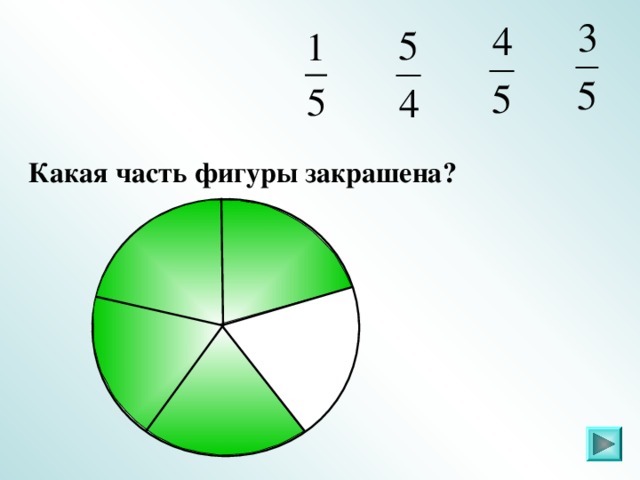
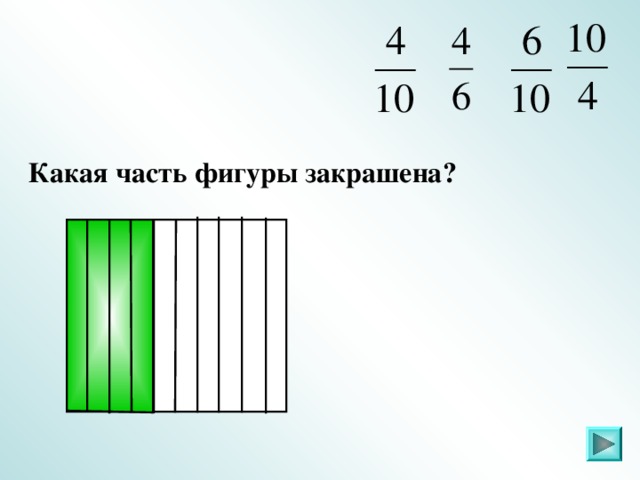
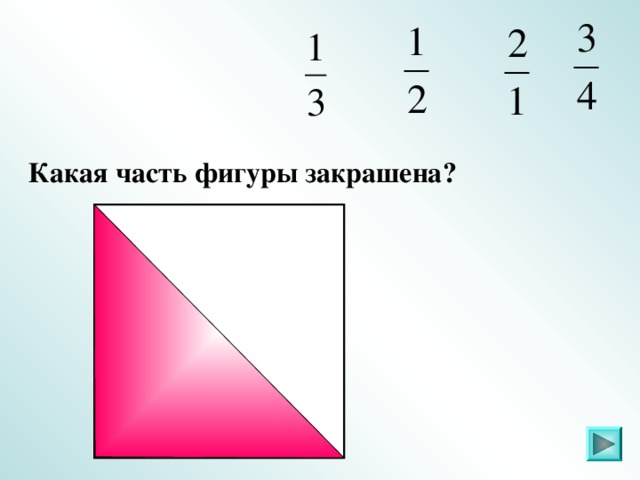
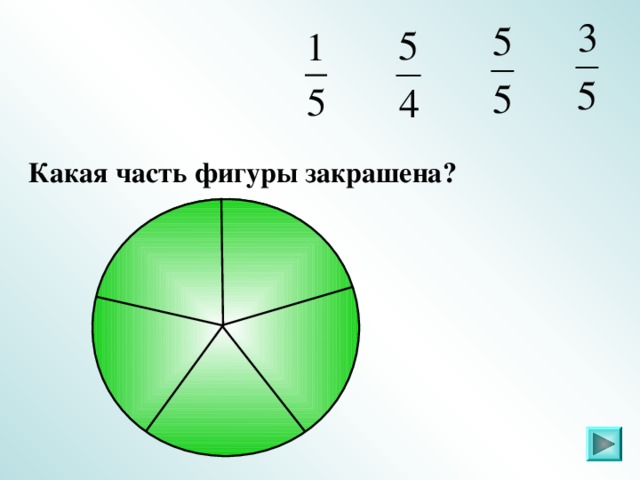
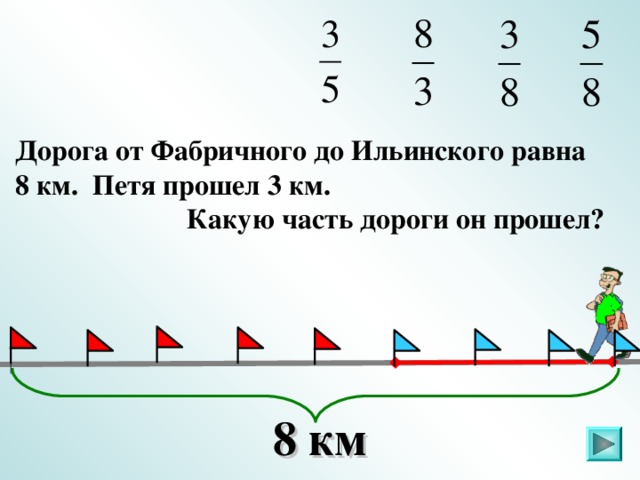
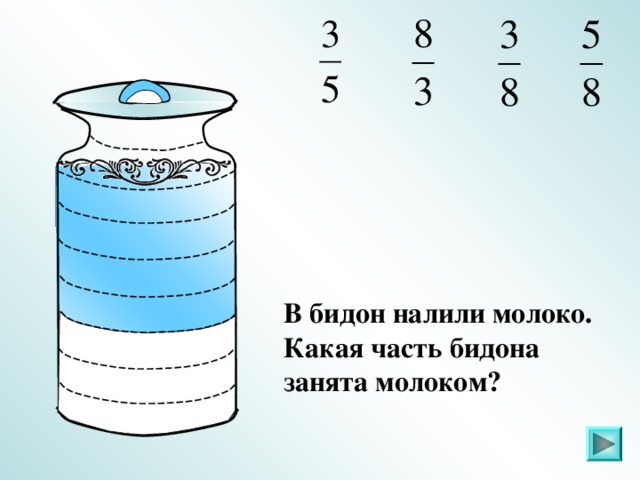
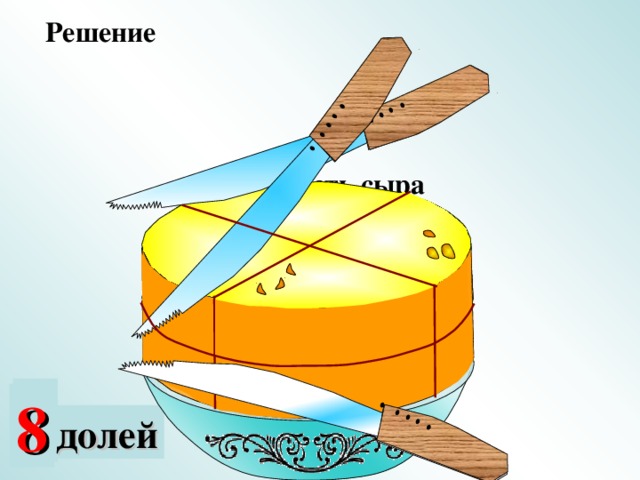
IV. Задание 2 . Какая часть фигуры закрашена (повторение)
Слайды 6 – 21.
Ответ:
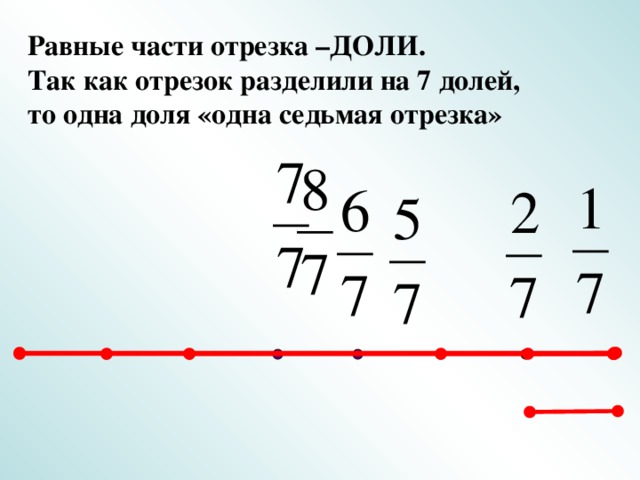
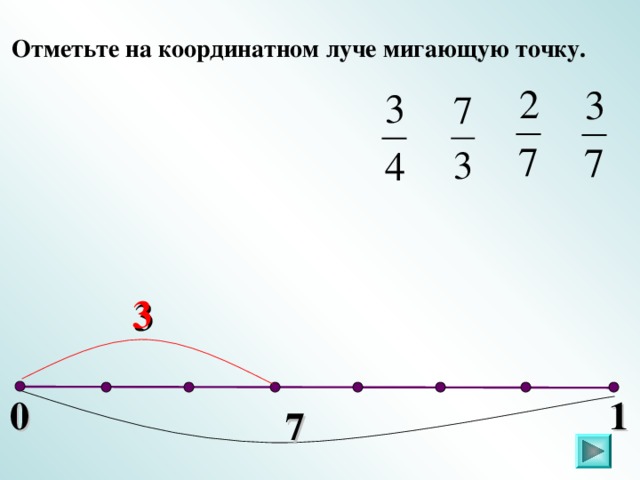
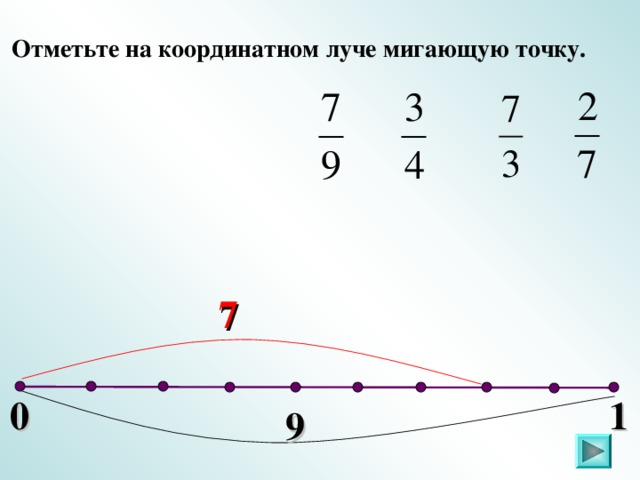
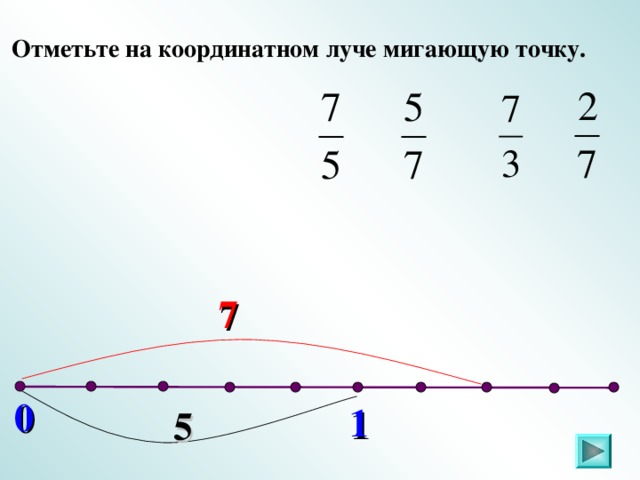
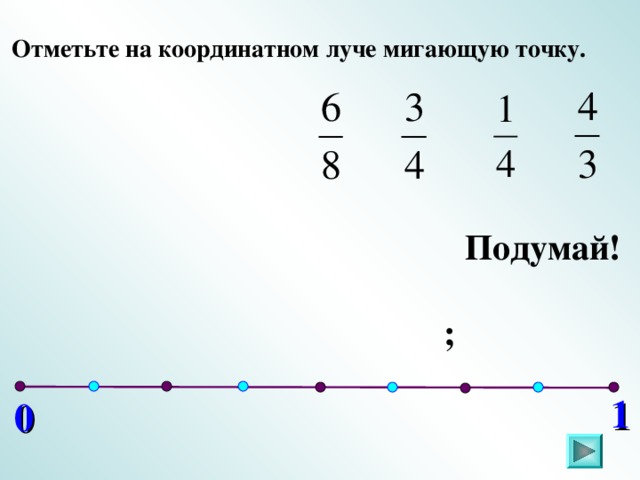
V. Обозначение дробей на координатном луче (повторение).
Слайды 22-26.
Решить № 893(если позволит время)
VI. Изучение нового материала.
Решение задач на нахождение дроби от числа.
№ 891(у доски)
Решение.
1ч.40 мин=60+40=100мин
- 100:5=20(мин) – на математику
- 100-20=80(мин) – осталось
- 80:4=209(мин) – на историю
Ответ: по 20 мин.
№ 901 (у доски)
1)20:5=4(км) составляет 1/5
2)4*2=8(км) – заасфальтировали
3)20-8=16(км) – осталось
VII. Итог урока.
VIII. Домашнее задание
Слайд № 27
Список использованной литературы и источников:
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: 5 класс. Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2012.