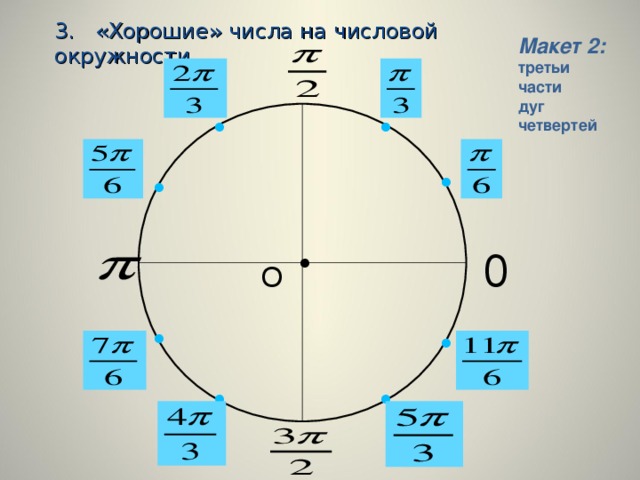
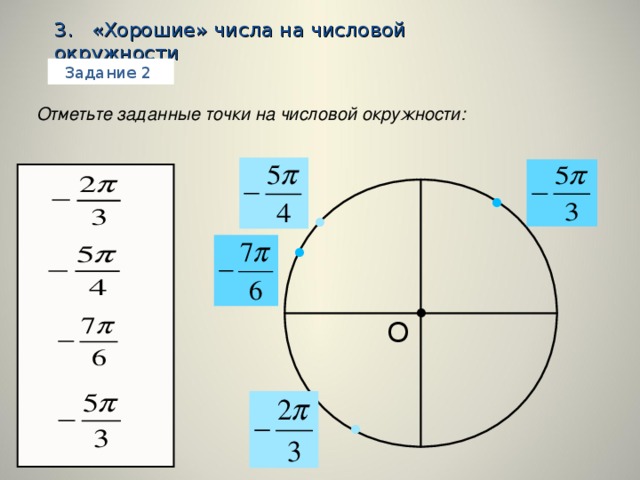
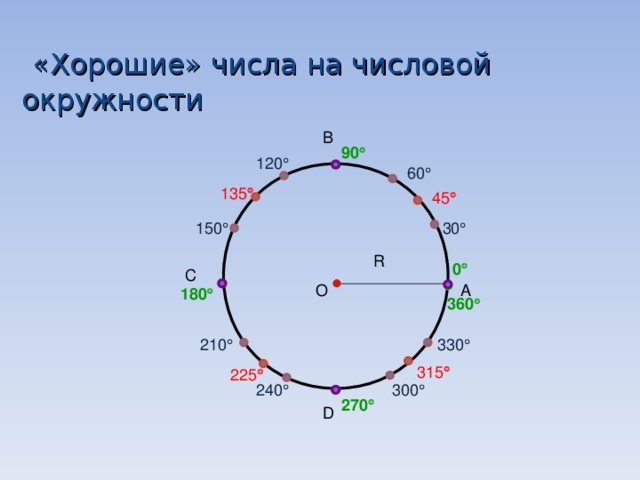
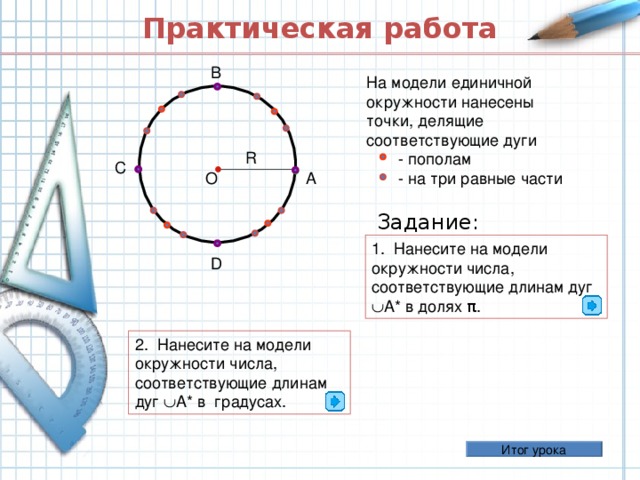
Презентация первого урока раздела "Тригонометрия". Введение понятия "числовая окружность" по учебнику А.Г. Мордкович 10 класс. Вводятся "отличные" и "хорошие" числа. Понятие как они находятся - залог успешного продвижения обучающихся по теме. Отработка умений производится через интерактивные слайды.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
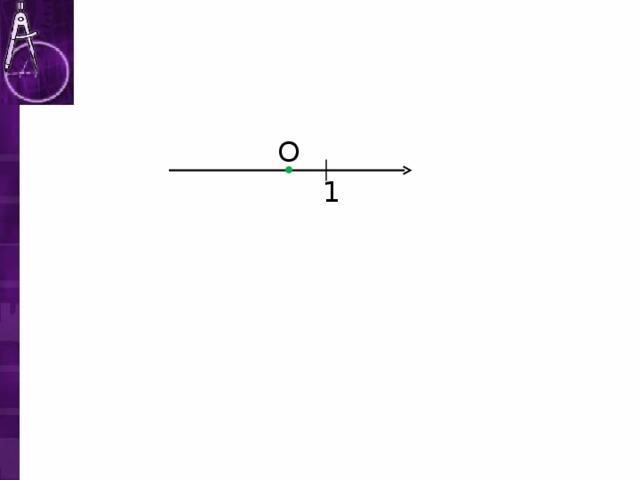
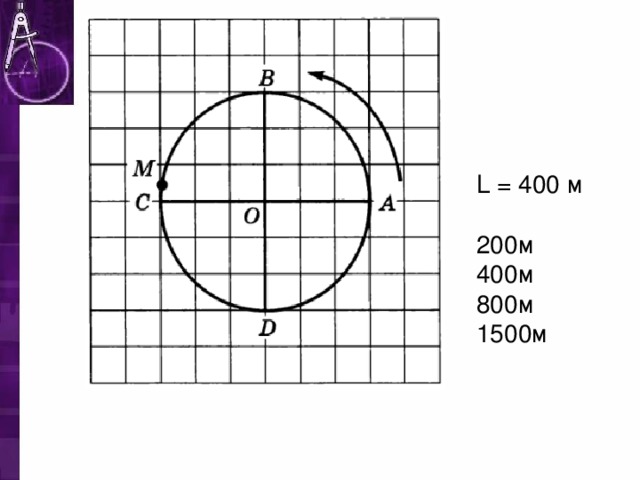
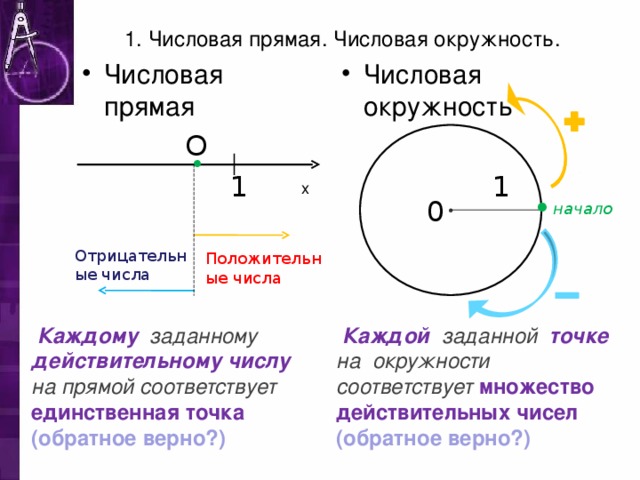
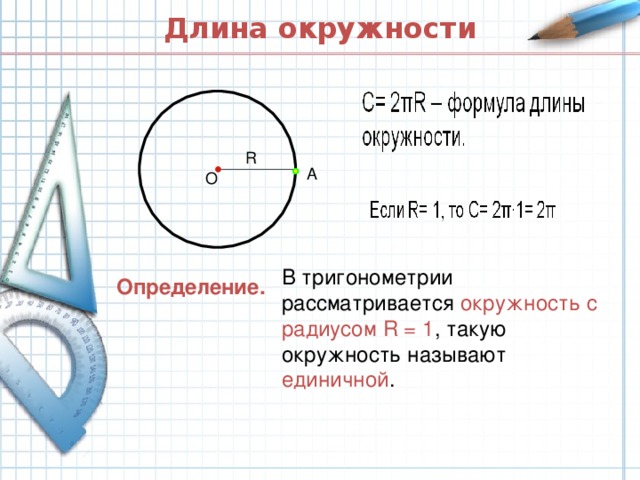
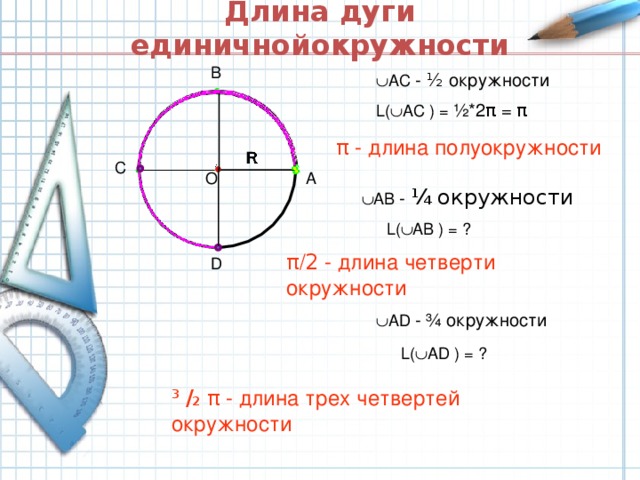
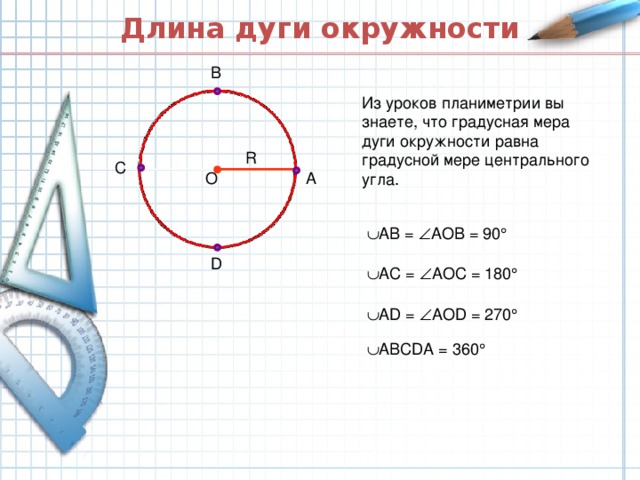
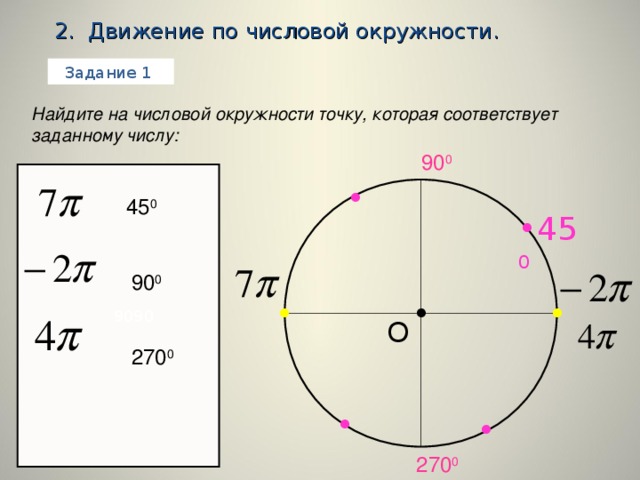
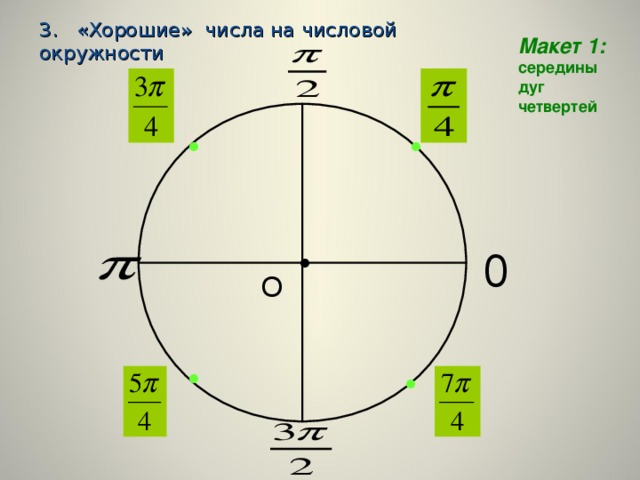
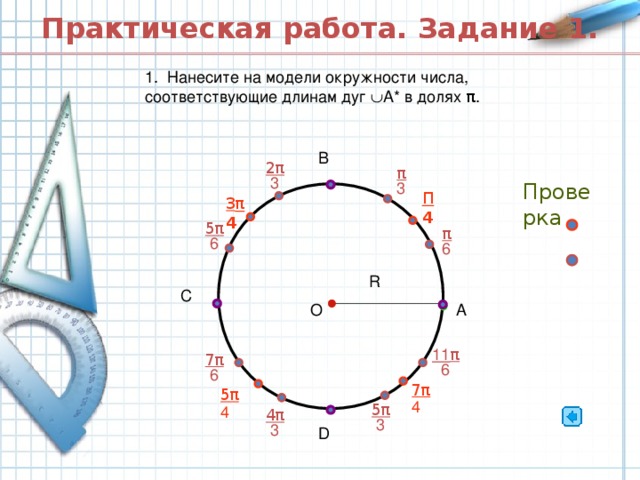
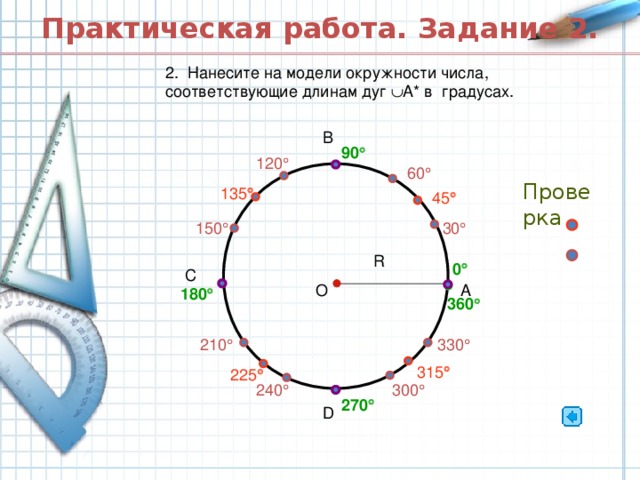
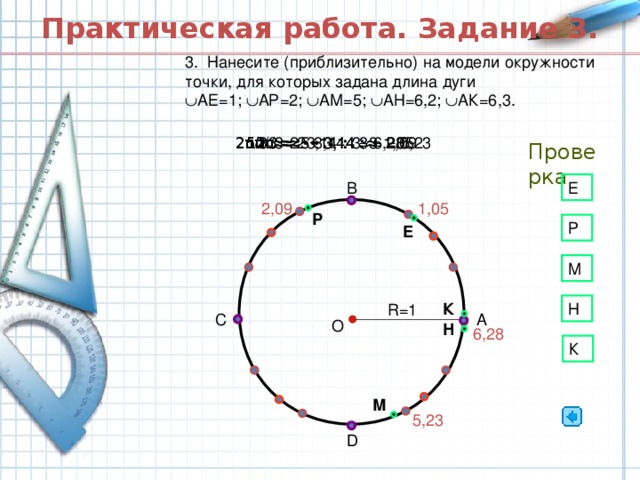
Числовая окружность. 10 класс.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Числовая окружность. 10 класс. »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1540 руб.
2560 руб.
1510 руб.
2510 руб.
1720 руб.
2860 руб.
1730 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства