Үшбұрыш теңсіздігі. Үшбұрыш теңсіздігі туралы теореманың дәлелдеуі.Есептер шығару
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Үшбұрыштар теңсіздігі
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Үшбұрыштар теңсіздігі»
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
2020 руб.
2880 руб.
2020 руб.
2880 руб.
2100 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
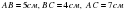 )
)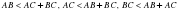

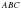 үшбұрышын қарастырып,
үшбұрышын қарастырып, 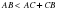 екенін дәлелдейік.
екенін дәлелдейік.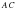 қаьырғасының созындысына
қаьырғасының созындысына 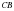 қабыырғасына тең
қабыырғасына тең 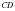 кесіндісін салайық.
кесіндісін салайық.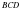 теңбүйірлі
теңбүйірлі  үшбұрышында
үшбұрышында 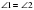 , ал
, ал 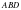 үшбұрышында
үшбұрышында 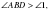 олай болса,
олай болса, 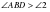 . Ал үшбұрышта үлкен қабырғаға қарсы үлкен бұрыш жататындықтан,
. Ал үшбұрышта үлкен қабырғаға қарсы үлкен бұрыш жататындықтан, 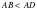 . Бірақ
. Бірақ 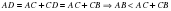 . Теорема дәлелденді.
. Теорема дәлелденді. 
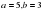 болса, үшінші қабырғасын тап.
болса, үшінші қабырғасын тап.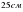 - ге, ал басқасы
- ге, ал басқасы 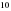 см- ге тең. Осылардың табаны қайсысы болады?
см- ге тең. Осылардың табаны қайсысы болады?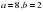 болса, үшінші қабырғасын тап.
болса, үшінші қабырғасын тап.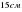 - ге, ал басқасы
- ге, ал басқасы 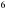 см- ге тең. Осылардың табаны қайсысы болады?
см- ге тең. Осылардың табаны қайсысы болады?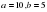 болса, үшінші қабырғасын тап.
болса, үшінші қабырғасын тап.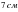 - ге, ал басқасы
- ге, ал басқасы 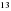 см- ге тең. Осылардың табаны қайсысы болады?
см- ге тең. Осылардың табаны қайсысы болады?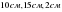
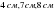
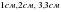 4.
4. 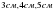
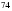 см, ал бір қабырғасы
см, ал бір қабырғасы 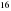 см- ге тең. Үшбұрыштың қалған екі қабырғасын табыңыз.
см- ге тең. Үшбұрыштың қалған екі қабырғасын табыңыз.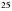 см- ге, екі қабырғасының айырмасы
см- ге, екі қабырғасының айырмасы 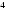 см- ге тең, ал оның сыртқы бұрыштарының бірі- сүйір бұрыш. Үшбұрыштың қабырғаларын табыңыз.
см- ге тең, ал оның сыртқы бұрыштарының бірі- сүйір бұрыш. Үшбұрыштың қабырғаларын табыңыз. 















