Рабочая программа учебного предмета «Математика» для 5 – 6 классов составлена на основе Федерального компонента государственного стандарта основного общего образования по математике, базисного учебного плана, примерной программы основного общего образовании по математике и авторской программы по математике для образовательных учреждений (5 – 6 классы): Программа. Планирование учебного материала. Математика. 5 – 6 классы. / авт. – сост. В. И. Жохов. – 2 – е издание, стер. – М.: Мнемозина, 2010.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Рабочая программа по математике 5-6 кл
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«рабочая программа по математике 5-6 кл »
Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа №2 с углубленным изучением отдельных предметов» города Губкина Белгородской области
РАБОЧАЯ ПРОГРАММА
по учебному предмету
«Математика»
(базовый уровень)
Основное общее образование: 5 – 6 классы
(ФКГОС)
Срок реализации: 2 года
Рабочая программа составлена на основе примерной программы основного общего образовании по математике и авторской программы по математике для 5 – 6 классов общеобразовательной школы. Авторы – составители: В. И. Жохов, - М.: Мнемозина, 2- е издание, 2010 г.
Составитель рабочей программы:
Есипова Ольга Анатольевна,
учитель математики
Губкин
2014 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Нормативные акты и учебно-методические документы, на основании которых разработана рабочая программа.
Рабочая программа учебного предмета «Математика» для 5 – 6 классов составлена на основе Федерального компонента государственного стандарта основного общего образования по математике, базисного учебного плана, примерной программы основного общего образовании по математике и авторской программы по математике для образовательных учреждений (5 – 6 классы): Программа. Планирование учебного материала. Математика. 5 – 6 классы. / авт. – сост. В. И. Жохов. – 2 – е издание, стер. – М.: Мнемозина, 2010.
Цели предмета в контексте основного общего образования.
Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и в развитии интеллекта, формировании личности каждого человека. Таким образом, значимость математической подготовки в общем образовании современного человека повлияла на следующие цели обучения математике в школе:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
формирование представлений о математических идеях и методах;
формирование представлений о математике как форме и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Целями изучения курса математики в 5 – 6-м классах являются: систематическое развитие понятия числа; выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики; подготовка учащихся к изучению систематических курсов алгебры и геометрии.
Задачи:
сохранить теоретические и методические подходы, оправдавшие себя в практике преподавания в начальной школе;
предусмотреть возможность компенсации пробелов в подготовке школьников и недостатков в их математическом развитии, развитии внимания и памяти;
обеспечить уровневую дифференциацию в ходе обучения;
обеспечить базу математических знаний, достаточную для изучения алгебры и геометрии, а также для продолжения образования;
сформировать устойчивый интерес учащихся к предмету;
выявить и развить математические и творческие способности;
развивать навыки вычислений с натуральными числами;
учить выполнять сложение и вычитание обыкновенных дробей с одинаковыми знаменателями, действия с десятичными дробями;
дать начальные представления об использование букв для записи выражений и свойств;
учить составлять по условию текстовой задачи, несложные линейные уравнения;
продолжить знакомство с геометрическими понятиями;
развивать навыки построения геометрических фигур и измерения геометрических величин.
Общая характеристика учебного предмета.
Курс математики в 5 – 6 классах, с одной стороны, является непосредственным продолжением курса математики начальной школы, систематизирует, обобщает и развивает полученные там знания, с другой стороны, позволяет учащимся адаптироваться к новому уровню изучения предмета, создает необходимую основу, на которой будут базироваться систематические курсы 7 – 9 классов.
Практическая значимость школьного курса математики 5 – 6 классов обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
Математика является одним из опорных предметов основной школы. Овладение учащимися системой математических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования. В первую очередь это относится к предметам естественнонаучного цикла, в частности к физике. Развитие логического мышления учащихся при обучении математике в 5 – 6 классах способствует усвоению предметов гуманитарного цикла. Практические умения и навыки арифметического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении математических абстракций, о соотношении реального и идеального, о характере отражения математической наукой явлений и процессов реального мира, о месте математики в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности воображения, математика развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения. Решение текстовых задач на всех этапах учебного процесса развивают творческие способности школьников.
Изучение математики в 5 – 6 классах позволяет формировать умения и навыки умственного труда: планирование своей работы, поиск рациональных путей её выполнения, критическую оценку результатов. В процессе изучения математики школьники учатся излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобретают навыки чёткого, аккуратного и грамотного выполнения математических записей.
Важнейшей задачей школьного курса математики является развитие логического мышления учащихся. Сами объекты математических умозаключений и правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Показывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, математика вносит значительный вклад в эстетическое воспитание учащихся.
Место учебного предмета в учебном плане.
В соответствии с учебным планом основного общего образования в курсе математики выделяются два этапа – 5 – 6 классы и 7 – 9 классы, у каждого из которых свои самостоятельные функции. В 5 – 6 классах изучается интегрированный предмет «Математика», в 7 – 9 классах – два предмета «Алгебра» и «Геометрия».
Федеральный Базисный учебный образовательный план для образовательных учреждений Российской Федерации предусматривает обязательное изучение математики на этапе основного общего образования в объеме 350 ч., в том числе в 5-х классах: всего 175 ч., в неделю – 5 часов; в 6-х классах: всего 175 ч., в неделю – 5 часов.
Данная рабочая программа рассчитана на 340 ч. на 2 года обучения.
Информация о внесенных изменениях в примерную и авторскую программу.
В связи с внесенными изменениями в годовой календарный график на 2014 – 2015 учебный год, организационный раздел ООП НОО, ООП ООО, учебный план на 2014 – 2015 учебный год (приказ по школе от 06.03.2014г.№ 314\1 «Об утверждении нормативных документов школы на 2013-2014 учебный год») в рабочую программу вносятся изменения. Количество часов по предмету «Математика» сокращается с 350 до 340 часов в связи с сокращением учебных недель с 35 до 34.
Изменения в рабочую программу не вносятся. Программа соответствует авторской: Программа. Планирование учебного материала. Математика. 5 – 6 классы. / авт. – сост. В. И. Жохов. – 2 – е издание, стер. – М.: Мнемозина, 2010.
Используемый УМК.
Математика. 5 класс/ Н. Я. Виленкин, В.И.Жохов, А.С.Чесноков, С. И. Шварцбурд – М.: Мнемозина, 2008.
Математика. 6 класс: учеб. для общеобразоват. учрежд. / Виленкин Н. Я., В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд/. - М.: Мнемозина, 2009.
Информация об используемых технологиях, формах и методах обучения, видах и формах контроля
| Технология | Ожидаемый результат | Практическое применение |
| Технология проектного обучения | Умение взаимодействовать в команде, распределять роли. Умения конструировать собственные знания, ориентироваться в информационном пространстве. Презентация результатов собственной деятельности. | Через создание проектов разного вида: Учебные, информационные, исследовательские, творческие, ролевые, игровые. |
| ИКТ – технологии | Экономия времени, наглядность, своевременный индивидуальный и фронтальный контроль усвоения темы, раздела. Повышение познавательного интереса обучающихся, создание ситуации успешности на уроке. | Презентации MS PowerPoint как лекции, задания, наглядность. Индивидуальное тестирование через программу My test. Работа в сети Интернет по поиску, классификации информации при создании проектов, изучения новой темы. |
| Технология интерактивного обучения | Постоянное, активное взаимодействие всех учащихся. | Моделирование жизненных ситуаций, использование ролевых игр, совместное решение проблем через работу в парах, дискуссии, дебаты, «аквариум», «карусель». |
| Здоровьесберегающие технологии | Сохранение и укрепление психического, интеллектуального, социального и физического здоровья обучающихся. | 1) строгая дозировка учебной нагрузки; смена форм и видов деятельности обучающихся (не менее 4 за урок), 2) построение урока с учетом динамичности учащихся, их работоспособности; четкая организация учебного труда, 3) соблюдение гигиенических требований (свежий воздух, оптимальный тепловой режим, хорошая освещенность, чистота); |
Технологии традиционного обучения применяются для освоения минимума содержания образования в соответствии с требованиями стандартов; технологии, построенные на основе объяснительно-иллюстративного способа обучения. В основе –информирование, просвещение обучающихся и организация их репродуктивных действий с целью выработки у школьников общеучебных умений и навыков.
Технологии дифференцированного обучения применяются для освоения учебного материала обучающимися, различающимися по уровню обучаемости, повышения познавательного интереса.
Технология проблемного обучения применяется с целью развития творческих способностей обучающихся, их интеллектуального потенциала, познавательных возможностей. Обучение ориентировано на самостоятельный поиск результата, самостоятельное добывание знаний, творческое, интеллектуально-познавательное усвоение учениками заданного предметного материала
Приоритетными формами и методами работы с обучающимися являются:
фронтальная работа, работа в малых группах (2-3 человека), проектная работа, исследовательская деятельность, информационно-поисковая деятельность (работа с дополнительными источниками информации: энциклопедиями, справочниками, словарями, научно-популярной литературой, ресурсами Internet), выполнение практических и лабораторных работ.
Используемые формы контроля- текущий и итоговый. Преобладающей формой текущего контроля выступает письменный (самостоятельные и контрольные работы, практические работы, тесты) и устный опрос (собеседование). Текущий контроль успеваемости обучающихся включает в себя поурочное и почетвертное (полугодовое) оценивание результатов их учебы. Промежуточная (годовая) аттестация представляет собой тестирования, контрольные работы, которые проводятся по итогам учебного года.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ УЧАЩИХСЯ
В результате изучения курса математики учащиеся должны:
в разделе: числа и вычисления
правильно употреблять термины, связанные с различными видами чисел и способами их записи: целое, дробное, рациональное, иррациональное, положительное, десятичная дробь и др.; переходить от одной формы записи чисел к другой (например, представлять десятичную дробь в виде обыкновенной, проценты – в виде десятичной или обыкновенной дроби);
сравнивать числа, упорядочивать наборы чисел; понимать связь отношений «больше» и «меньше» с расположением точек на координатной прямой;
выполнять арифметические действия с рациональными числами, находить значения степеней; сочетать при вычислениях устные и письменные приемы;
составлять и решать пропорции, решать основные задачи на дроби, проценты;
округлять целые числа и десятичные дроби, производить прикидку результата вычислений.
в разделе: выражения и их преобразования
правильно употреблять термины «выражение», «числовое выражение», «буквенное выражение», «значение выражения», понимать их использование в тексте, в речи учителя, понимать формулировку заданий: «упростить выражение», «найти значение выражения», «разложить на множители»;
составлять несложные буквенные выражения и формулы; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; выражать из формул одни переменные через другие;
находить значение степени с натуральным показателем.
в разделе: уравнения и неравенства
понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики;
правильно употреблять термины «уравнение», «неравенство», «корень уравнения»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить уравнение, неравенство»;
решать линейные уравнения с одной переменной.
в разделе: функции
познакомиться с примерами зависимостей между реальными величинами (прямая и обратная пропорциональности, линейная функция);
познакомиться с координатной плоскостью, знать порядок записи координат точек плоскости и их названий, уметь построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости;
находить в простейших случаях значения функций, заданных формулой, таблицей, графиком;
интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.
в разделе: геометрические фигуры и их свойства, измерение геометрических величин
распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, многоугольники, окружности, круги); изображать указанные геометрические фигуры; выполнять чертежи по условию задачи;
владеть практическими навыками использования геометрических инструментов для изображения фигур, а также для нахождения длин отрезков и величин углов;
решать задачи на вычисление геометрических величин (длин, углов, площадей, объемов), применяя изученные свойства фигур и формулы.
Учебно - тематический план
| № п / п | Класс | Наименование тем | Часы учебного времени | Проведение контрольных работ для каждого класса |
| 1 | 5 | Повторение. | | Входная контрольная работа. |
| 2 | 5 | Натуральные числа и шкалы. | 15 | |
| | | Обозначение натуральных чисел. | 2 | |
| | | Отрезок. Длина отрезка. Треугольник. | 4 | |
| | | Плоскость, прямая, луч. | 2 | |
| | | Шкалы и координаты. | 3 | |
| | | Меньше или больше. | 4 | Контрольная работа №1. |
| 3 | 5 | Сложение и вычитание натуральных чисел. | 21 | |
| | | Сложение натуральных чисел и его свойства. | 5 | |
| | | Вычитание. | 5 | Контрольная работа №2. |
| | | Числовые и буквенные выражения. | 3 | |
| | | Буквенная запись свойств сложения и вычитания. | 3 | |
| | | Уравнение. | 5 | Контрольная работа №3 |
| 4 | 5 | Умножение и деление натуральных чисел. | 27 | |
| | | Умножение натуральных чисел и его свойства. | 5 | |
| | | Деление. | 7 | |
| | | Деление с остатком. | 4 | Контрольная работа №4. |
| | | Упрощение выражений. | 5 | |
| | | Порядок выполнения действий. | 3 | |
| | | Квадрат и куб. | 3 | Контрольная работа №5. |
| 5 | 5 | Площади и объемы. | 12 | |
| | | Формулы. | 2 | |
| | | Площадь. Формула площади прямоугольника. | 2 | |
| | | Единицы измерения площадей. | 3 | |
| | | Прямоугольный параллелепипед. | 1 | |
| | | Объемы. Объем прямоугольного параллелепипеда. | 4 | Контрольная работа №6. |
| 6 | 5 | Обыкновенные дроби. | 23 | |
| | | Окружность и круг. | 2 | |
| | | Доли. Обыкновенные дроби. | 4 | |
| | | Сравнение дробей. | 3 | |
| | | Правильные и неправильные дроби. | 3 | Контрольная работа №7. |
| | | Сложение и вычитание дробей с одинаковыми знаменателями. | 3 | |
| | | Деление и дроби. | 2 | |
| | | Смешанные числа. | 2 | |
| | | Сложение и вычитание смешанных чисел. | 4 | Контрольная работа №8. |
| 7 | 5 | Десятичные дроби. Сложение и вычитание десятичных дробей. | 13 | |
| | | Десятичная запись дробных чисел. | 2 | |
| | | Сравнение десятичных дробей. | 3 | |
| | | Сложение и вычитание десятичных дробей. | 5 | |
| | | Приближенные значения чисел. Округление чисел. | 3 | Контрольная работа №9. |
| 8 | 5 | Умножение и деление десятичных дробей. | 26 | |
| | | Умножение десятичных дробей на натуральные числа. | 3 | |
| | | Деление десятичных дробей на натуральные числа. | 6 | Контрольная работа №10. |
| | | Умножение десятичных дробей. | 5 | |
| | | Деление десятичных дробей. | 7 | |
| | | Среднее арифметическое. | 5 | Контрольная работа №11. |
| 9 | 5 | Инструменты для вычислений и измерений. | 17 | |
| | | Микрокалькулятор. | 2 | |
| | | Проценты. | 6 | Контрольная работа №12. |
| | | Угол. Прямой и развернутый угол. Чертежный треугольник. | 3 | |
| | | Измерение углов. Транспортир. | 3 | |
| | | Круговые диаграммы. | 3 | Контрольная работа №13. |
| 10 | 5 | Итоговое повторение курса математики 5-го класса | 15 | Контрольная работа №14. |
| | | Итого | 170 | |
| 10 | 6 | Повторение. | 2 | Входная контрольная работа. |
| 11 | 6 | §1.Делимость чисел. | 20 | |
| | | Делители и кратные 9. | 3 | |
| | | Признаки делимости на 10, на 5 и на 2. | 3 | |
| | | Признаки делимости на 9 и на 3. | 2 | |
| | | Простые и составные числа. | 2 | |
| | | Разложение на простые множители. | 2 | |
| | | Наибольший общий делитель. Взаимно простые числа. | 3 | |
| | | Наименьшее общее кратное. | 5 | Контрольная работа №1. |
| 12 | 6 | § 2. Сложение и вычитание дробей с разными знаменателями | 22 | |
| | | Основное свойство дроби. | 2 | |
| | | Сокращение дробей. | 3 | |
| | | Приведение дробей к общему знаменателю. | 3 | |
| | | Сравнение, сложение и вычитание дробей с разными знаменателями. | 7 | Контрольная работа №2 |
| | | Сложение и вычитание смешанных чисел. | 7 | Контрольная работа №3. |
| 13 | 6 | § 3. Умножение и деление обыкновенных дробей | 32 | |
| | | Умножение дробей. | 5 | |
| | | Нахождение дроби от числа. | 4 | |
| | | Применение распределительного свойства умножения. | 6 | Контрольная работа №4 |
| | | Взаимно обратные числа. | 2 | |
| | | Деление. | 6 | Контрольная работа №5 |
| | | Нахождение числа по его дроби. | 5 | |
| | | Дробные выражения. | 4 | Контрольная работа №6 |
| 14 | 6 | § 4. Отношения и пропорции | 19 | |
| | | Отношения. | 5 | |
| | | Пропорции. | 3 | |
| | | Прямая и обратная пропорциональные зависимости. | 4 | Контрольная работа №7 |
| | | Масштаб. | 2 | |
| | | Длина окружности и площадь круга. | 2 | |
| | | Шар. | 3 | Контрольная работа №8 |
| 15 | 6 | § 5. Положительные и отрицательные числа | 13 | |
| | | Координаты на прямой. | 3 | |
| | | Противоположные числа. | 2 | |
| | | Модуль числа. | 2 | |
| | | Сравнение чисел. | 3 | |
| | | Изменение величин. | 3 | Контрольная работа №9 |
| 16 | 6 | § 6. Сложение и вычитание положительных и отрицательных чисел | 11 | |
| | | Сложение чисел с помощью координатной прямой. | 2 | |
| | | Сложение отрицательных чисел. | 2 | |
| | | Сложение чисел с разными знаками. | 3 | |
| | | Вычитание. | 4 | Контрольная работа №10 |
| 17 | 6 | § 7. Умножение и деление положительных и отрицательных чисел | 12 | |
| | | Умножение. | 3 | |
| | | Деление. | 3 | |
| | | Рациональные числа. | 3 | Контрольная работа№11 |
| | | Свойства действий с рациональными числами. | 3 | |
| 18 | 6 | § 8. Решение уравнений | 15 | |
| | | Раскрытие скобок. | 3 | |
| | | Коэффициент. | 3 | |
| | | Подобные слагаемые. | 4 | Контрольная работа №12 |
| | | Решение уравнений. | 5 | Контрольная работа №13 |
| 19 | 6 | § 9. Координаты на плоскости | 13 | |
| | | Перпендикулярные прямые. | 2 | |
| | | Параллельные прямые. | 2 | |
| | | Координатная плоскость. | 3 | |
| | | Столбчатые диаграммы. | 2 | |
| | | Графики. | 4 | Контрольная работа №14 |
| 20 | 6 | Итоговое повторение курса математики 5 – 6-го классов. | 11 | Контрольная работа №15. |
| | | Всего: | 170 | |
| | | Итого за 5 – 6 класс: | 340 | |
СОДЕРЖАНИЕ УЧЕБНОГО КУРСА
5 класс (170 часов)
1. Натуральные числа и шкалы (15 ч).
Обозначение натуральных чисел. Отрезок, длина отрезка. Треугольник. Плоскость, прямая, луч. Шкалы и координаты. Меньше или больше.
Основная цель – систематизировать и обобщить сведения о натуральных числах, полученные в начальной школе; закрепить навыки построения и измерения отрезков
2.Сложение и вычитание натуральных чисел (21 ч).
Сложение натуральных чисел и его свойства. Вычитание. Решение текстовых задач. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнение.
Основная цель – закрепить и развить навыки сложения и вычитания натуральных чисел.
3. Умножение и деление натуральных чисел (27 ч).
Умножение натуральных чисел и его свойства. Деление. Деление с остатком. Упрощение выражений. Порядок выполнения действий. Степень числа. Квадрат и куб числа.
Основная цель – закрепить и развить навыки арифметических действий с натуральными числами
4. Площади и объемы (12 ч).
Формулы. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объемы. Объем прямоугольного параллелепипеда.
Основная цель – расширить представление учащихся об измерении геометрических величин на примере вычисления площадей и объемов, систематизировать известные им сведения о единицах измерения.
5. Обыкновенные дроби (23 ч).
Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковыми знаменателями .Деление и дроби. Смешанные числа. Сложение и вычитание смешанных чисел.
Основная цель – познакомить учащихся с понятием дроби в объеме, достаточном для введения десятичных дробей.
6. Десятичные дроби. Сложение и вычитание десятичных дробей (13 ч).
Десятичная запись дробных чисел. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Приближённые значения чисел. Округление чисел.
Основная цель – выработать умение читать, записывать, сравнивать, округлять десятичные дроби, выполнять сложение и вычитание десятичных дробей.
7. Умножение и деление десятичных дробей (26 ч).
Умножение десятичных дробей на натуральные числа. Деление десятичных дробей на натуральные числа. Умножение десятичных дробей. Деление на десятичную дробь. Среднее арифметическое.
Основная цель – выработать умение умножать и делить десятичные дроби, выполнять задания на все действия с натуральными числами и десятичными дробями
8. Инструменты для вычислений и измерений (17 ч).
Микрокалькулятор. Проценты. Угол. Прямой и развернутый угол. Чертёжный треугольник. Измерение углов. Транспортир. Круговые диаграммы.
Основная цель – сформировать умения решать простейшие задачи на проценты, выполнять измерение и построение углов.
9. Повторение. Решение задач. (16 ч).
6 класс (170 часов)
1. Делимость чисел (20 ч).
Делители и кратные числа. Общий делитель и общее кратное. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители.
Основная цель – завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения — прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36 = 6· 6 = 4· 9 = 2 ·18 и т. п. Умения разложить число на простые множители не обязательно добиваться от всех учащихся.
2. Сложение и вычитание дробей с разными знаменателями (22 ч).
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Сложение и вычитание дробей. Решение текстовых задач.
Основная цель – выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.
3. Умножение и деление обыкновенных дробей (31 ч).
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель – выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.
4. Отношения и пропорции (19 ч).
Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятия о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.
Основная цель – сформировать понятия пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
5. Положительные и отрицательные числа (13 ч).
Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Изображение чисел на координатной прямой. Координата точки.
Основная цель – расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
6. Сложение и вычитание положительных и отрицательных чисел (11 ч).
Сложение и вычитание положительных и отрицательных чисел.
Основная цель – выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
7. Умножение и деление положительных и отрицательных чисел (12 ч).
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. Десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений.
Основная цель – выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь — в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как .
8. Решение уравнений (15 ч).
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель – подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.
9. Координаты на плоскости (13 ч).
Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель – познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
10. Повторение. Решение задач (14 ч).
ФОРМЫ И СРЕДСТВА КОНТРОЛЯ
Устный счёт. Устный опрос. Фронтальный опрос. Индивидуальное задание. Математический тест. Математический диктант. Практическая работа.
Преобладающими формами текущего контроля являются самостоятельные работы, тестирование. Тематика самостоятельных и тестовых работ охватывает всю программу по математике 5 – 6 классов, и их полный набор служит хорошим помощником при контроле и коррекции полученных знаний, навыков и умений учащихся. Самостоятельные работы используются и как карточки для индивидуальной работы, так как содержат не более 2 заданий и не занимают много времени от урока (7-10 минут).
Итоговый контроль – экзамен в форме письменной контрольной работы.
Критерии оценивания достижений учащихся.
Единые нормы являются основой при оценке как контрольных, так и всех других письменных работ по математике. Применяется индивидуальный подход к оценке каждой письменной работы учащегося, обращается внимание на качество выполнения работы в целом, а затем уже на количество ошибок и на их характер.
Оценка письменной работы определяется с учётом прежде всего её общего математического уровня, оригинальности, последовательности, логичности её выполнения, а также числа ошибок и недочётов и качества оформления работы.
Ошибка, повторяющаяся в одной работе несколько раз, рассматривается как одна ошибка.
За орфографические ошибки, допущенные учениками, оценка не снижается; об орфографических ошибках доводится до сведения преподавателя русского языка. Однако ошибки в написании математических терминов, уже встречавшихся школьникам класса, должны учитываться как недочёты в работе.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
к негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного – из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка повышается за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
5 класс
Входное тестирование по математике 5 класс.
Вариант 1.
Отметь число, записанное суммой разрядных слагаемых:
8 000 + 500 + 60+ 5 .
| 1) 80 565 | 2) 850 065 | 3) 8 565 | 4) 800 565 |
Запиши числа в порядке возрастания: 704, 7 040, 7 004, 407, 7 404, 7 400.
Найди значение выражения 8 204 – 3 657 , выбери правильный ответ.
1) 4 547 2) 4 647 3) 4 557 4) 5 547
Найди частное чисел 5600 и 80, отметь ответ.
1) 70 2) 44 800 3) 700 4) 5 520
Какой знак нужно поставить вместо * , чтобы равенство
7 * 0 = 0 было верным?
1) + 2) – 3) ∙ 4) ׃
Лифт может поднять только 4 человека. Какое наименьшее количество раз поднимется лифт, чтобы перевезти 37 человек?
1) 8 2) 9 3) 10 4) 11
За какое время мотоциклист проедет 120 км, если за 1 ч он проезжает 40 км? Выбери ответ на вопрос.
1) 3 км 2) 80 ч 3) 3 ч 4) 30 ч
Найди значение выражения 600 + 900׃ 9 - 8 = …. Запиши ответ.
Поставь в выражении скобки 600 + 900׃9 - 8, чтобы значение выражения было равно 1500.
Дорожные рабочие выложили асфальтом 39 км дороги, что составляет третью часть всей дороги. Сколько километров осталось выложить?
1) 13 км 2) 78 км 3) 117 км 4) 26 км.
Вариант 2.
Отметь число, записанное суммой разрядных слагаемых: 4 000 + 700 + 30+ 6.
1) 400 736 2) 470 036 3) 40 736 4) 4 736.
Запиши числа в порядке убывания: 806, 8 060, 8 006, 608, 8 606, 8 600.
Найди значение выражения 6 102 – 2 468 , выбери правильный ответ.
1) 3 644 2) 4 634 3) 3 634 4) 3 734
Найди произведение 480 и 60, отметь ответ.
1) 420 2) 8 3) 28 800 4) 2 880
Какой знак нужно поставить вместо * , чтобы равенство 9 * 0 = 0 было верным?
1) ׃ 2) ∙ 3) - 4) +Грузовая машина перевозит за 1 рейс 5 тонн песка. Сколько рейсов необходимо сделать, чтобы перевезти 28 тонн песка?
1) 4 2) 5 3) 6 4) 7
За какое время машина проедет 360 км, если за 1 ч она проезжает 60 км? Выбери ответ на вопрос.
1) 6 км 2) 60 ч 3) 6 ч 4) 420 ч.
Найди значение выражения 900 - 600׃6+9 =. Запиши ответ.
Поставь в выражении скобки 900-600׃6+9, чтобы значение выражения было равно 59.
В вазе лежало 85 ягод черешни. Ребята съели пятую часть всех ягод. Сколько ягод осталось в вазе?
1) 17 2) 425 3) 102 4) 68.
Контрольная работа №1 «Натуральные числа и шкалы».
Вариант 1
1. Начертите отрезок АС и отметьте на нем точку В. Измерьте отрезки АВ и АС.
2. Постройте отрезок MN = 2 см8 мм и отметьте на нем точки K и P так, чтобы точка P лежала между точками M и K.
3. Отметьте точки D и E и проведите через них прямую. Начертите луч OC, пересекающий прямую DE, и луч MK, не пересекающий прямую DE.
4. На координатном луче, единичный отрезок которого равен длине одной клетки тетради, отметьте точки А (2), В (6), S (8), D (11). На этом же луче отметьте точку Р, если ее координата – натуральное число, которое больше 11, но меньше 13.
5. Найдите четырехзначное число, оканчивающееся цифрой 9. Известно, что это число меньше 1 019.
Вариант 2
1. Начертите отрезок МХ и отметьте на нем точку С. Измерьте отрезки МХ и СХ.
2. Постройте отрезок АВ = 6 см2 мм и отметьте на нем точки D и C так, чтобы точка D лежала между точками C и В.
3. Отметьте точки Р и К и проведите луч КР. Начертите прямую MN, пересекающую луч КР, и прямую АВ, не пересекающую луч КР.
4. На координатном луче, единичный отрезок которого равен длине одной клетки тетради, отметьте точки М (3), Р (5), С (7), N (10). На этом же луче отметьте точку Т, если ее координата – натуральное число, которое меньше 10, но больше 8.
5. Запишите число, оканчивающееся цифрой 8, которое больше любого трехзначного числа и меньше 1 018.
Вариант 3
1. Начертите отрезок NY и отметьте на нем точку D. Измерьте отрезки ND и DY.
2. Постройте отрезок DC = 3 см4 мм и отметьте на нем точки A и B так, чтобы точка B лежала между точками D и A.
3. Отметьте точки M и N и проведите через них прямую. Начертите луч AB, пересекающий эту прямую, и луч DC, не пересекающий её.
4. На координатном луче, единичный отрезок которого равен длине одной клетки тетради, отметьте точки С (4), D (6), E (8), F (12). На этом же луче отметьте точку M, если ее координата – натуральное число, которое больше 12, но меньше 14.
5. Запишите число, оканчивающееся цифрой 7, зная, что оно меньше пятизначного числа и больше 9 987.
Вариант 4
1. Начертите отрезок АС и отметьте на нем точку К. Измерьте отрезки АК и КС.
2. Постройте отрезок ВC = 2 см5 мм и отметьте на нем точки D и E так, чтобы точка D лежала между точками E и C.
3. Отметьте точки D и E и проведите луч ED. Начертите прямую MN, пересекающую луч ED, и прямую KP, не пересекающую луч ED.
4. На координатном луче, единичный отрезок которого равен длине одной клетки тетради, отметьте точки M (13), N (9), D (6), K (1). На этом же луче отметьте точку S, если ее координата – натуральное число, которое меньше 12, но больше 10.
5. Запишите пятизначное число, оканчивающееся цифрой 7. Известно, что это число больше 99 988.
Контрольная работа № 2 «Сложение и вычитание натуральных чисел»
Вариант 1
1. Выполните действия: а) 562 987 + 34 267;
б) 56 008 – 4 789; в) (64 231 + 45 989) – 5 989.
2. Сравните значения выражений:
14 534 – (5 765 + 3 610) и 14 534 – (5 769 + 3 610).
3. Одна сторона треугольника равна 28 см, вторая на 8 см меньше первой, а третья – на 2 см меньше второй. Найдите периметр треугольника.
4. В автобусе было 98 пассажиров. На первой остановке вышло 15 и вошло 27 пассажиров, на второй остановке вышло 24 и вошло 18 пассажиров. Сколько пассажиров стало в автобусе после второй остановки?
5.Найдите число, которое при увеличении втрое увеличится на 24.
Вариант 2
1. Выполните действия: а) 671 980 + 27 651;
б) 67 021 – 5 396; в) (65 895 + 4 334) – 5 895.
2. Сравните значения выражений:
53 107 – (3 409 + 2 537) и 53 107 – (3 409 + 2 533)
3. Одна сторона треугольника равна 34 см, вторая на 2 см больше первой, а третья – на 4 см меньше первой. Найдите периметр треугольника.
4. В автобусе было 98 пассажиров. На первой остановке вышло 27 и вошло 14 пассажиров, на второй остановке вышло 17 и вошло 25 пассажиров. Сколько пассажиров стало в автобусе после второй остановки?
5.Найдите число, которое при уменьшении на 24 уменьшится вдвое.
Контрольная работа №3 «Числовые и буквенные выражения. Уравнения».
Вариант 1
1. Решите уравнение:
а) 320 – х = 176; б) (у + 383) – 479 = 332.
2. Упростите выражение:
а) 376 + у + 128; б) 573 – (а + 173).
3. Составьте уравнение и решите задачу:
На автостоянке было х машин. Когда с нее уехало 27 машин и приехало 19, то стало 63 машины. Сколько машин было на автостоянке первоначально?
4. Составьте буквенное выражение для решения задачи: Длина ломанной АВСD равна 68 см. Звено АВ равно 16см, а звено ВС на а см длиннее звена АВ. Найдите длину звена CD. Упростите выражение и вычислите при а = 24.
5. Задумали некоторое число. Из 167 вычли задуманное число, из полученной разности вычли 53 и получили 29. Какое число было задумано?
6.* Угадайте корень уравнения 
= 8 и выполните проверку.
Вариант 2
1. Решите уравнение:
а) 543 + у = 812; б) 821 – (х + 268) =349.
2. Упростите выражение:
а) 574 + т + 249; б) 748 – (с + 248).
3. Составьте уравнение и решите задачу:
В канистре было х литров бензина. Когда в нее доли 22 л, а затем отлили 14 л, в ней стало 45 л бензина. Сколько литров бензина было в канистре первоначально?
4. Составьте буквенное выражение для решения задачи: Длина ломанной KLMN равна 73 см. Звено KL равно 18см, звено LM на b см длиннее звена KL. Найдите длину звена MN. Упростите выражение и вычислите при b = 12.
5. Задумали некоторое число. К 125 прибавили задуманное число, из полученной суммы вычли 39 и получили 87. Какое число было задумано?
6.* Угадайте корень уравнения = 3 и выполните проверку.
Контрольная работа №4 «Умножение и деление натуральных чисел»
Вариант 1
1. Вычислите:
а) 97 . 132 + 686 : 98; б) 37 596 – 8 064 : 16 . 74; в) 123 000 : 100.
2. Решите уравнение:
а) х : 18 = 352; б) 4у – 29 = 31; в) 48 : (65 – с) = 12
3. Решите с помощью уравнения задачу: На складе было 783 т цемента. Ежедневно с него вывозили по 27 т, после чего осталось 351 т цемента. Сколько дней со склада вывозили цемент?
4. Как изменится частное, если делимое уменьшить в 2 раза, а делитель – в 4 раза?
Вариант 2
1. Вычислите:
а) 69 . 143 – 776 : 97; б) 13 904 – 2 842 : 14 . 68; в) 479 000 : 1000.
2. Решите уравнение:
а) 266 : х = 14; б) 6у + 47 = 119; в) (127 – с) : 4 = 24
3. Решите с помощью уравнения задачу: На овощной базе было 927 кг картофеля. В течение 16 дней с нее забирали по одному мешку картофеля, после чего осталось 159 кг. Какова масса мешка картофеля?
4. Как изменится частное, если делимое увеличить в 2 раза, а делитель – в 6 раза?
Контрольная работа №5 «Упрощение выражений. Квадрат и куб числа»
Вариант 1
1. Найдите значение выражения:
а) 798 . 349 – 798 . 249; б) 57 . 38 – 8640 : 24 + 66;
в) 52 + 33.
2. Упростите выражение: 31а + 127 + 48а. Вычислите при а = 4, а = 10.
3. Решите уравнения: а) 17х – 4х = 195;
б) 5х + 23х = 168; в) (3х + 10х) . 8 = 312.
4. Решите задачу с помощью уравнения: В двух корзинах 98 яблок. В первой яблок в 6 раз меньше, чем во второй. Сколько яблок в каждой корзине?
5*. Угадайте корень уравнения: 2х = 32.
Вариант 2
1. Найдите значение выражения:
а) 684 . 397 – 584 . 397; б) 39 . 58 – 9720 : 27 + 33;
в) 52 + 33.
2. Упростите выражение: 23т + 174 + 68т. Вычислите при т = 8, т = 100.
3. Решите уравнения: а) 7х + 41х = 192;
б) 40х – 4х = 540; в) (9х + 7х) . 6 = 288.
4. Решите задачу с помощью уравнения: В книге на 30 страницах напечатаны две сказки. Первая занимает в 4 раза больше страниц, чем вторая. Сколько страниц занимает каждая сказка?
5*. Угадайте корень уравнения: 3х = 27.
Контрольная работа №6 «Площади и объемы»
Вариант 1
1. Используя формулу пути s = vt, найдите:
а) путь s, если t = 12 ч, v =105 км/ч;
б) скорость v, если s = 168 м и t = 14 мин.
2. Ширина прямоугольного участка земли 500 м, и она меньше длины на 140 м. Найдите площадь участка и выразите ее в гектарах.
3. Ширина прямоугольного параллелепипеда 12 см, длина в 3 раза больше, а высота на 3 см больше ширины. Найдите объем прямоугольного параллелепипеда.
4. Найдите значение выражения
15 600 : 65 + 240 . 86 – 20 550.
5. Ширина прямоугольника 23 см. На сколько увеличится площадь этого прямоугольника, если его длину увеличить на 3 см?
Вариант 2
1. Используя формулу пути s = vt, найдите:
а) путь s, если t = 13 ч, v =408 км/ч;
б) время t , если v = 800 м/мин, s = 7200 м
2. Длина прямоугольного участка земли 650 м, а ширина на 50 м меньше. Найдите площадь участка и выразите ее в гектарах.
3. Длина прямоугольного параллелепипеда 45 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины. Найдите объем прямоугольного параллелепипеда.
4. Найдите значение выражения
17 040 – 69 . 238 – 43 776 : 72.
5. Длина прямоугольника 84 см. На сколько уменьшится площадь этого прямоугольника, если его ширину уменьшить на 5 см?
Контрольная работа №7 «Правильные и неправильные дроби. Сравнение дробей»
Вариант 1.
1. Примите за единичный отрезок длину 8 клеток тетради и отметьте на координатном луче точки: А; М ; К ; D F .
2. Сравните числа:
а) б) в) ; г) .
3. Сложите числа 30 и числа 14.
4. При каких натуральных значениях а будет правильной дробь ?
5. Ширина прямоугольника 48 см, что составляет его периметра. Найдите длину этого прямоугольника.
Вариант 2
Примите за единичный отрезок длину 12 клеток тетради и отметьте на координатном луче точки: В ;С ; Е ; Р ; R .
2. Сравните числа:
а) б) в) ; г) .
3. Сложите числа 18 и числа 40.
4. При каких натуральных значениях а будет правильной дробь ?
5. Длина прямоугольника 80 см, что составляет его периметра. Найдите ширину этого прямоугольника.
Контрольная работа №8 «Сложение и вычитание смешанных чисел»
Вариант 1
1. Найдите значение выражения .
2.Решите уравнение: .
3. Преобразуйте число в неправильную дробь.
4. Представьте число в виде смешанного числа.
5. Найдите корень уравнения и представьте его в виде смешанного числа:
.
6. Рома выполнял домашние задания 3 ч, из них математику ч, а родной язык ч. Сколько времени затратил Рома на остальные предметы?
Вариант 2
1.Найдите значение выражения .
2.Решите уравнение: .
3. Преобразуйте число в неправильную дробь.
4. Представьте число в виде смешанного числа.
5. Найдите корень уравнения и представьте его в виде смешанного числа:
.
6.Из 6 соток дачного участка сотки занимают постройки, сотки – грядки, а остальную площадь – газон. Сколько соток занимает газон?
Контрольная работа №9 « Сложение и вычитание десятичных дробей»
Вариант А1
1. Выполните действия:
а) 43,58 – 18,693 + 20,3; б) (2,08 + 3,69) – 1,08.
2. Решите уравнения:
а) 45 – х = 38,783; б) (х + 1,7) – 6,02 = 10,4.
3. Собственная скорость лодки равна 8,7 км/ч, а скорость течения равна 2,9 км/ч. Найдите скорость лодки по течению и против течения.
4. Округлите каждое из чисел а) 584,356; б) 935,0846; в) 0,8355 до единиц, до десятых и до сотых.
5. Замените звездочку цифрой так, чтобы получилось верное неравенство: 9,1 9,*9.
Вариант А2
1. Выполните действия:
а) 62,49 – 29,584 + 30,4; б) (5,09 + 8,37) – 4,09.
2. Решите уравнения:
а) х + 27,621 = 38; б) (8,3 – х) – 0,02 = 3,4.
3. Собственная скорость байдарки равна 8,9 км/ч, а скорость течения равна 3,2 км/ч. Найдите скорость байдарки по течению и против течения.
4. Округлите каждое из чисел
а) 573,856; б) 846,0739; в) 0,325 до единиц, до десятых и до сотых.
5. Замените звездочку цифрой так, чтобы получилось верное неравенство: 7,*9
Вариант Б1
1. Выполните действия:
а) 37,873 – 24,5061 + 431,2; б) 20,04 – (6,064 + 10,04).
2. Решите уравнения:
а) 3,97х + 20,4х + 0,63х = 5 050; б) 80,6 – (х – 7,98) = 63,4.
3. Скорость течения реки равна 2,8 км/ч, а скорость катера по течению – 16,7 км/ч. Найдите собственную скорость катера и его скорость против течения.
4. Округлите каждое из чисел
а) 54,38709; б) 532,34453; в) 93,5959 до сотен, до сотых и до тысячных.
5. Какие одинаковые цифры можно поставить вместо звездочек, чтобы получить верное неравенство: 6,*3
Вариант Б2
1. Выполните действия:
а) 57,938 – 42,6502 + 764,3; б) 40,02 – (5,087 + 30,02).
2. Решите уравнения:
а) 12,7х + 2,06х + 0,24х = 4 545;
б) (52,3 – х) – 4,08 = 17,3.
3. Скорость течения реки равна 2,9 км/ч, а скорость катера против течения – 26,4 км/ч. Найдите собственную скорость катера и его скорость по течению.
4. Округлите каждое из чисел а) 93,43509; б) 612,72371; в) 54,7995 до сотен, до сотых и до тысячных.
5. Какие одинаковые цифры можно поставить вместо звездочек, чтобы получить верное неравенство: 5,4* 5,*4.
Контрольная работа №10 «Умножение и деление десятичных дробей на натуральные числа»
Вариант 1
1. Вычислите:
а) 6,08 . 37; б) 49,15 . 60; в) 19,19 : 19; г) 6 : 32
2. Выполните действия: 8,2 – 0,96 : 8 . 60
3. Решите уравнения:
а) 6х + 3,8 = 58,4; б) (39,38 – х) : 9 = 4,02
4. 5 машин песка и 3 машины щебня имеют массу 22,8 т. Найдите массу одной машины щебня, если масса одной машины песка равна 2,7 т.
5. Сумма двух чисел равна 16,2, а разность – 2,6. Найдите эти числа.
Вариант 2
1. Вычислите:
а) 7,09 . 28; б) 32,75 . 40; в) 28,28 : 14; г) 9 : 48
2. Выполните действия: 7,6 – 0,98 : 7 . 40
3. Решите уравнения:
а) 8х – 4,9 = 52,7; б) (х + 14,22) : 6 = 3,07
4. 4 пакета картофеля и 3 пакета моркови имеют массу 15,8 кг. Найдите массу одного пакета моркови, если масса одного пакета картофеля равна 2,6 кг.
5. Сумма двух чисел равна 14,6, а разность – 2,8. Найдите эти числа.
Контрольная работа №11 «Умножение и деление десятичных дробей»
Вариант 1
1. Вычислите:
а) 0,872 6,3; в) 0,045 0,1; д) 0,702 : 0,065;
б) 1,6 7,625; г) 30,42 : 7,8; е) 0,026 : 0,01.
2. Найдите среднее арифметическое чисел 32,4; 41; 27,95; 46,9; 55,75.
3. Найдите значение выражения 296,2 – 2,7 6,6 + 6 : 0,15.
4. Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
5. Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найдите среднее арифметическое всех этих девяти чисел.
Вариант 2
Вычислите:
а) 0,964 7,4; в) 0,72 0,01; д) 0,0918 : 0,0085;
б) 2,4 7,375; г) 25,23 : 8,7; е) 0,39 : 0,1.
2. Найдите среднее арифметическое чисел 63; 40,63; 70,4; 67,97.
3. Найдите значение выражения 398,6 – 3,8 7,7 + 3 : 0,06.
4. Легковой автомобиль шел 2 ч со скоростью 55,4 км/ч и еще 4 ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.
5. Среднее арифметическое пяти чисел 4,7, а сумма других трех чисел 25,14. Найдите среднее арифметическое всех этих восьми чисел.
Вариант 3
Вычислите:
а) 0,738 9,7; в) 0,081 0,1; д) 0,0988 : 0,0095;
б) 3,6 5,125; г) 28,13 : 9,7; е) 0,052 : 0,01.
2. Найдите среднее арифметическое чисел 52; 38,3; 43,24; 49,6; 58,86.
3. Найдите значение выражения 575,4 – 4,3 8,8 + 9 : 0,18.
4. Велосипедист ехал 4 ч со скоростью 12,3 км/ч и 2 ч со скоростью 11,7 км/ч. Найдите среднюю скорость велосипедиста на всем пути.
5. Сумма четырех чисел 9,36, а среднее арифметическое семи других чисел 1,9. Найдите среднее арифметическое всех этих одиннадцати чисел.
Вариант 4
1. Вычислите:
а) 0,687 8,6; в) 0,69 0,01; д) 0,795 : 0,0075;
б) 3,2 6,875; г) 32,83 : 6,7; е) 0,83 : 0,1.
2. Найдите среднее арифметическое чисел 85,37; 49; 63,2; 76,43.
3. Найдите значение выражения 483,6 – 3,6 9,9 + 4 : 0,08.
4. Моторная лодка плыла 3 ч со скоростью 17,9 км/ч и 5 ч со скоростью 18,7 км/ч. Найдите среднюю скорость лодки на всем пути.
5. Среднее арифметическое трех чисел 7,6, а сумма четырех других чисел 12,69. Найдите среднее арифметическое всех этих семи чисел.
Контрольная работа №12 «Проценты»
Вариант 1
1.Площадь поля 260 га. Горохом засеяно 35 % поля. Какую площадь занимают посевы гороха?
2.Найдите значение выражения 201 – (176,4 : 16,8 + 9,68) 2,5.
3.В библиотеке 12 % всех книг – словари. Сколько книг в библиотеке, если словарей в ней 900?
4.Решите уравнение 12 + 8,3х + 1,5х = 95,3.
5.От мотка провода отрезали сначала 30 %, а затем еще 60 % остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?
Вариант 2
1.В железной руде содержится 45 % железа. Сколько тонн железа содержится в 380 т руды?
2.Найдите значение выражения (299,3 : 14,6 – 9,62) 3,5 + 72,2.
3.За день вспахали 18 % поля. Какова площадь всего поля, если вспахали 1170 га?
4.Решите уравнение 6,7у + 13 + 3,1у = 86,5.
5.Израсходовали сначала 40 % имевшихся денег, а затем еще 30 % оставшихся. После этого осталось 105 р. Сколько денег было первоначально?
Вариант 3
1.В олимпиаде по математике участвовали 120 учащихся пятых и шестых классов. Пятиклассники составляют 55 % всех участников. Сколько пятиклассников приняло участие в олимпиаде?
2.Найдите значение выражения 161 – (469,7 : 15,4 + 9,52) 1,5.
3.В таксомоторном парке 16 % всех машин – «Москвичи». Сколько там всего машин, если «Москвичей» в нем 40?
4.Решите уравнение 14 + 6,2а + 2,4а = 69,9.
5.Турист прошел сначала 60 % намеченного пути, а затем еще 20 % оставшегося. После этого ему осталось пройти 8 км. Какой путь должен был пройти турист?
Вариант 4
1.Объем бочки равен 540 л. Водой заполнили 85 % этой бочки. Сколько литров воды налили в бочку?
2.Найдите значение выражения (534,6 : 13,2 – 9,76) 4,5 + 61,7.
3.За контрольную работу по математике было поставлено 15 % пятерок. Сколько учеников писало контрольную работу, если пятерки получили шестеро учеников?
4.Решите уравнение 3,7а + 15 + 4,1а = 89,1.
5.В первый день вспахали 30 % поля, а во второй день 40 % остатка. После этого осталось вспахать 252 га. Какова площадь поля?
Контрольная работа №13 «Угол прямой и развернутый.Транспортир»
Вариант 1
Постройте углы, если: а) ВМЕ = 68; б) СКР = 115.
Начертите AKN такой, чтобы А = 120. Измерьте и запишите градусные меры остальных углов треугольника.
Луч ОК делит прямой угол DOS на два угла так, что угол DOK составляет 0,7 угла DOS. Найдите градусную меру угла KOS.
Развернутый угол AMF разделен лучом МС на два угла АМС и CMF. Найдите градусные меры этих углов, если угол АМС вдвое больше угла CMF.
Из вершины развернутого угла DKP проведены его биссектриса КВ и луч КМ так, что ВКМ = 38. Какой может быть градусная мера угла DKM ?
Вариант 2.
Постройте углы, если: а) ADF = 110; б) HON = 73.
Начертите BCF такой, чтобы В = 105. Измерьте и запишите градусные меры остальных углов треугольника.
Луч АР делит прямой угол CAN на два угла так, что угол NAP составляет 0,3 угла CAN. Найдите градусную меру угла PAC.
Развернутый угол BOE разделен лучом OT на два угла BOT и TOE. Найдите градусные меры этих углов, если угол BOT втрое меньше угла TOE.
Из вершины развернутого угла MNR проведены его биссектриса NB и луч NP так, что ВNP = 26. Какой может быть градусная мера угла MNP ?
Вариант 3
Постройте углы, если: а) CDN = 83; б) XOP = 120.
Начертите BCD, в котором С = 135. Измерьте и запишите градусные меры остальных углов треугольника.
Луч NB делит прямой угол MNK на два угла так, что угол KNB составляет 0,6 угла MNK. Найдите градусную меру угла MNB.
Развернутый угол ADE разделен лучом DX на два угла АDX и XDE. Найдите градусные меры этих углов, если угол АDX втрое больше угла XDE.
Из вершины развернутого угла BDM проведена биссектриса DE и луч DC так, что CDE = 19. Какой может быть градусная мера угла BDC?
Вариант 4
Постройте углы, если: а) DKL = 95; б) KMN = 59.
Начертите POC, в котором О = 110. Измерьте и запишите градусные меры остальных углов треугольника.
Луч DB делит прямой угол XDE на два угла так, что
угол XDB составляет 0,4 угла XDE. Найдите градусную меру угла BDE.Развернутый угол NPK разделен лучом PR на два угла NPR и RPK. Найдите градусные меры этих углов, если угол NPR в два раза меньше угла RPK.
Из вершины развернутого угла XYZ проведена биссектриса YO и луч YR так, что OYR = 33. Какой может быть градусная мера угла XYR?
Итоговая контрольная работа №14 5 класс.
Вариант 1
Часть I
1. Сравните числа: 2,85 и 2,45.
А. 2,85 2,45. В. 2,85 = 2,45. Г. 2,45 2,85.
2. Округлив 12,34 до десятых, получим…
А. 12,30. Б. 12,3. В. 12. Г. 12,4.
3. Решите уравнение 87,4 : х = 2,3.
Ответ:__________
4. Сумма и равна…
А. Б. 6. В. Г.
5. На рисунке изображены различные виды углов. Назовите соответственно название каждого из них.
1) 2) 3)
_____________ ___________ _________
А. тупой Б. развёрнутый В. острый
6. В библиотеке было 9550 книг. Детские книги составляли 32%. Сколько детских книг было в библиотеке?
Ответ:____________
7. При переводе обыкновенной дроби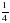 
в десятичную получается…
А. 0,25. Б. 0,025. В. 2,5. Г. 25.
8. Упростите выражение 1,8а – 1,5а + 1,7а и найдите его значение при а = 3,12.
Ответ:__________
9. Найдите среднее арифметическое чисел 34,5; 32,7; 30,9.
А. 98,1. Б. 32,7. В. 327. Г. 3,27.
10. Найдите значение выражения 3,6 . 2,3 + 3,6 . 7,7 наиболее удобным способом.
Ответ:___________
Часть II
1. (2 балла) Решите уравнение (10,9 – х) : 0,46 = 2,5.
2. (6 баллов) Собственная скорость моторной лодки 6,7 км/ч, скорость течения реки 1,2 км/ч. Лодка плыла 2 ч против течения и 2 ч по течению реки. Какой путь проплыла моторная лодка за эти 4 часа?
Вариант 2.
Часть I
1. Сравните числа: 28,732 и 28,67.
А. 28,732
В. 28,67 28,732. Г. 28,732 28,67.
2. Округляя до десятков число 278,73, получим…
А. 280. Б. 270. В. 278,7. Г. 278,8.
3. В результате упрощения выражения получается
А. . Б. В. . Г. .
4. Решите уравнение: 13,44 : х = 2,4
Ответ:__________
На рисунке изображен угол. Как он называется?
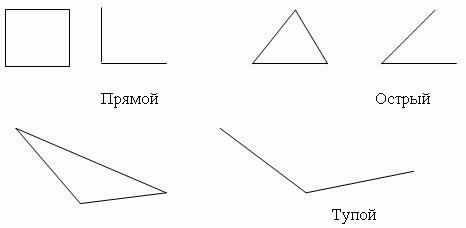
А. тупой Б. развёрнутый В. острый
6. Вычислите наиболее удобным способом: 255,85 : 0,01 + 44,15 : 0,01.
Ответ:_________
7. Теплоход проплыл 70 км по реке за 2 ч м 90 км за 3 ч. С какой средней скоростью проплыл теплоход весь путь?
А. 32 км/ч. Б. 36 км/ч. В. 34 км/ч. Г. 38 км/ч.
8. Найдите сумму неполного частного и остатка от деления числа 387 на 17.
Ответ:____________
9. В первый день турист прошёл всего пути. Сколько километров прошёл турист в первый день, если всего он прошёл 28 км?
А. 16 км. Б. 12 км. В. 14 км. Г. 10 км.
10. Автотурист проехал в первый день 120 км, что составляет 15% намеченного пути. Какова длина намеченного пути?
А. 180 км. Б. 800 км. В. 1200км. Г. 1800 км.
Часть II
1. (2 балла) Решите уравнение: (4,5 – х) . 5,8 = 8,7.
2. (6 баллов) С трёх участков собрали 87,36 т капусты. При этом с первого участка собрали в 1,4 раза больше, а со второго – в 1,8 раза больше, чем с третьего участка. Сколько тонн капусты собрали с каждого участка?
Вариант 3
Часть I
1. Сравните числа: 28,5 и 28,9
А. 28,9 28,5 В. 28,9 = 28,5 Г. 28,5 28,9.
2. Округлив 9,96 до десятых, получим…
А. 9,0. Б. 9,9. В. 10,0. Г. 10.
3. Решите уравнение: 2,3 . х = 105,8.
Ответ:___________
4. Угол на рисунке называется…
________________
А. Прямым. Б. Тупым. В. Развёрнутым. Г. Острым.
5. Укажите соответствие между числами и их названиями.
1) 2) 0,25. 3) 7
А. Натуральное число. Б. Смешанное число. Г. Десятичная дробь.
6. Площадь поля 500 га. Горохом засеяли 65% поля. Какую площадь поля засеяли горохом?
Ответ:___________
7. Если неполное частное равно 6, делитель 15, а остаток 4, то результат деления записывается в виде смешанного числа…
А. Б. В. Г.
8. Разность и равна…
А. 
Б. В. Г. 6.
9. Найдите среднее арифметическое чисел: 13,8; 14,2; 14,3.
А. 42,3. Б. 14,1. В. 141. Г. 1,41.
10. Найдите значение выражения 23,47 . 0,1 – 13,47 . 0,1 наиболее удобным способом.
Ответ:_________
Часть II
1. (2 балла) Решите уравнение: (7,8 – х) : 0,65 = 1,2.
2. (6 баллов) Катер шёл 3 ч против течения реки и 2 ч по течению. Какой путь прошёл катер за эти 5 ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3 км/ч?
Вариант 4
Часть I
1. Сравните числа: 27, 372 и 27,51.
А. 27,372 27,51. Б. 27,372 = 27,51.
В. 27,372
2. Округляя число 10,273 до десятых, получим…
А. 10,0. Б. 10,2. В. 10,4. Г. 10,3.
3. Разность чисел 15 – равна…
А. Б. В. Г. .
4. Решите уравнение: 5,8 + 2х = 8,6.
Ответ:__________
5. Укажите соответствие между величинами и названиями углов.
1) 2) 3) 4)
А. Острый. Б. Тупой. В. Прямой. Г. Развёрнутый.
6. Найдите значение выражения 28,73 . 0,1 – 24,53 . 0,1 наиболее удобным способом.
Ответ:_________
7. Найдите среднее арифметическое чисел: 13,8; 14,5; 14,9.
А. 43,2. Б. 1,44. В. 144. Г. 14,4.
8. Если неполное частное равно 12, делитель 5, а остаток 3, то результат деления записывается в виде смешанного числа…
А. Б. В. Г. .
9. Представьте обыкновенную дробь в виде десятичной и найдите значение выражения : 0,2.
А. 3,75. Б. 37,5. В. 0,365. Г. 375.
10. В цистерне 2000 л бензина, 3,5% бензина ушло на заправку автомобиля. Сколько литров ушло на заправку автомобиля?
Ответ:_____________
Часть II
1. (2 балла) Решите уравнение: (9,1 – х) : 0,64 = 1,5.
2. (6 баллов) Среднее арифметическое трёх чисел равно 6. Найдите эти числа, если первое число в 2,5 раза больше, а второе в 1,5 раза больше третьего.
Ответы
Часть I
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вариант 1 | Б | Б | х = 38 | Б | БВА | 3056 книг | А | 6,24 | Б | 36 |
| Вариант 2 | Г | А | Б | х = 5,6 | А | 30 000 | А | 35 | Г | Б |
| Вариант 3 | Б | В | х = 46 | В | БГА | 325 га | В | А | Б | 1 |
| Вариант 4 | В | Г | А | х = 1,4 | ВАГБ | 0,42 | Г | Б | А | 70 л |
Часть II.
| | 1 | 2 |
| Вариант 1 | х = 9,75 | 26,8 км |
| Вариант 2 | х = 3 | 20,8 т – III; 37,44 т – II; 29,12 т - I |
| Вариант 3 | х = 7,02 | 91,7 км |
| Вариант 4 | х = 8,14 | 3,6 – III; 5,4 – II; 9 – I |
Для оценивания результатов выполнения работ учащимися применяются два количественных показателя: традиционная отметка («2», «3», «4» и «5») и рейтинг: от 0 до 18 баллов, назначение рейтинга – расширение диапазона традиционной отметки.
Рейтинг формируется путём подсчёта общего количества баллов, полученных учащимися за выполнение первой и второй частей работы.
Критерии оценивания.
| Отметка | Количество баллов |
| «3» | 7 – 9 |
| «4» | 10 – 14 |
| «5» | 15 – 18 |
Время выполнения работы и условия её проведения
На выполнение работы отводится 45 минут. Учащимся выдаются тексты первой и второй частей работы, которые выполняются последовательно.
| № урока | Вид контроля | Тема | Источник | Страница |
| 92 | Тест | Обыкновенные дроби. | Контрольно – измерительные материалы. Математика 5 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2014. – 96 с. | 44 – 45 |
| 110 | Тест | Сложение и вычитание десятичных дробей. | Контрольно – измерительные материалы. Математика 5 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2014. – 96 с. | 58 – 59 |
| 119 | Тест | Умножение и деление десятичных дробей на натуральное число. | Контрольно – измерительные материалы. Математика 5 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2014. – 96 с. | 62 – 63 |
| 133 | Тест | Умножение и деление десятичных дробей. | Контрольно – измерительные материалы. Математика 5 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2014. – 96 с. | 68 – 69 |
6 класс
Входное тестирование по алгебре 6 класс.
Вариант 1.
Вычислите .
Вычислите 34707 : 69
Представьте в виде неправильной дроби 7.
Замените неправильную дробь смешанным числом.
Вычислите 3,34 + 28,7.
Вычислите .
Вычислите 20,4 : 0,8
Округлите число 0,6539до сотых.
Расположите в порядке убывания числа 3,78; 3,784; 3,7801.
Выразите в метрах 0,002 км.
Найдите площадь квадрата, сторона которого 11 см.
Сколько процентов составляет число 17 от 100?
В магазин привезли 62 т картофеля. До обеда продали 15% всего количества. Сколько картофеля осталось еще продать?
22 ученика класса, что составляет 55% всего количества, учатся без троек. Сколько человек в классе?
Один из смежных углов равен 230. Вычислите градусную меру второго смежного угла.
Вычислите 52 + 22.
Вариант 2.
Вычислите .
Вычислите 18252 : 36
Представьте в виде неправильной дроби 4.
Замените неправильную дробь смешанным числом.
Вычислите 6,35 – 3,5.
Вычислите .
Вычислите 20,7 : 0,9
Округлите число 0,2513до десятых.
Расположите в порядке убывания числа 1,4302; 1,43; 1,437.
Выразите в тоннах 16 кг.
Найдите периметр квадрата, сторона которого 13 см.
Сколько процентов составляет число 13 от 100?
В магазин привезли 28 т картофеля. До обеда продали 18% всего количества. Сколько картофеля осталось еще продать?
В заводском цехе работают 18 женщин, что составляет 45% всех рабочих цеха. Сколько всего рабочих в цехе?
Один из смежных углов равен 1030. Вычислите градусную меру второго смежного угла.
Вычислите 62 – 22.
Контрольная работа №1: «Делимость чисел»
Вариант 1.
Найдите:
а) наибольший общий делитель чисел 24 и 18;
б) наименьшее общее кратное чисел 12 и 15.
Разложите на простые множители число 546.
Какую цифру можно записать вместо звездочки в числе 681*, чтобы оно
а) делилось на 9; б) делилось на 5; в) было кратно 6.
Выполните действия:
а) 7 – 2,35 + 0,435; б) 1,763 : 0,086 – 0,34 16.
Найдите произведение чисел а и b, если их наименьшее общее кратное равно 420, а наибольший общий делитель равен 30.
Вариант 2.
Найдите:
а) наибольший общий делитель чисел 28 и 42;
б) наименьшее общее кратное чисел 20 и 25.
Разложите на простые множители число 510.
Какую цифру можно записать вместо звездочки в числе 497*, чтобы оно
а) делилось на 3; б) делилось на 10; в) было кратно 9.
Выполните действия:
а) 9 – 3,46 + 0,535; б) 2,867: 0,094 + 0,31 15.
Найдите наименьшее общее кратное чисел m и n, если их произведение равно 7 200, а наибольший общий делитель равен 40.
Контрольная работа №2: «Сравнение, сложение и вычитание дробей с разными знаменателями»
Вариант 1.
Сократите:
Выполните действия: а) б) в) .
Решите уравнение: а) ; б) 5,86x + 1,4x = 76,23
В первые сутки теплоход прошел всего пути, во вторые сутки – на пути больше, чем впервые. Какую часть всего пути теплоход прошел за эти двое суток?
Найдите четыре дроби, каждая из которых больше и меньше .
Вариант 2.
Сократите: .
Выполните действия: а) ; б) ; в) .
Решите уравнение: а) ; б) 6,28y – 2,8y = 36,54.
В первый день засеяли всего поля, во второй день засеяли на поля меньше, чем в первый. Какую часть поля засеяли за эти два дня?
Найдите четыре дроби, каждая из которых больше и меньше .
Контрольная работа №3: «Сложение и вычитание смешанных чисел»
Вариант 1.
Сравните числа: а) б) в)
Найдите значение выражения:
а) б) в) г)
На автомашине планировали перевезти сначала т груза, а потом еще т. Однако перевезли на т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине?
Решите уравнение:
а) б) .
Представьте дробь в виде суммы трех дробей, у каждой из которых числитель равен 1.
Вариант2.
Сравните числа: а) б) в) 0,72 и
Найдите значение выражения:
а) б) в) г) .
С одного опытного участка рассчитывали собрать т пшеницы, а с другого т. Однако с них собрали на т больше. Сколько тонн пшеницы собрали с этих двух участков?
Решите уравнение:
а) б)
Представьте дробь в виде суммы трех дробей, у каждой из которых числитель равен 1.
Контрольная работа №4: «Умножение дробей. Нахождение дроби от числа»
Вариант 1.
1. Найдите произведение:
а) ; б) ; в) .
2. Выполните действия: .
3. Фермерское хозяйство собрало 960 т зерна. 75% собранного зерна составляла пшеница, а остатка – овса. Сколько тонн овса собрало фермерское хозяйство?
4. В один пакет насыпали кг сахара, а в другой - в 4 раза больше. На сколько больше сахара насыпали во второй пакет, чем в первый?
5. Не приводя к общему знаменателю, сравните дроби и .
Вариант 2.
1. Найдите произведение:
а) ; б) ; в) .
Выполните действия: .
3. Во время субботника заводом было выпущено 150 холодильников. этих холодильников было отправлено в больницы, а 60% остатка – в детские сады. Сколько холодильников было отправлено в детские сады?
4. Масса гуся кг, а масса страуса в 7 раз больше. На сколько килограммов масса гуся меньше массы страуса?
5. Не приводя к общему знаменателю, сравните дроби: и .
Контрольная работа №5 «Деление обыкновенных дробей»
Вариант 1.
Выполните действия:
а) б) в)
г) д) .
За кг конфет заплатили 15 р. Сколько стоит 1 кг этих конфет?
Решите уравнение:
а) б) ( 3,1x + x) : 0,8 = 2,05.
У Сережи и Пети всего 69 марок. У Пети марок в раза больше, чем у Сережи. Сколько марок у каждого из мальчиков?
Представьте в виде дроби выражение .
Вариант 2.
Выполните действия:
а) б) в)
г) д) .
За кг печенья заплатили 6 р. Сколько стоит 1 кг этого печенья?
Решите уравнение:
а) б) ( 7,1у – у) : 0,6 = 3,05.
В два железнодорожных вагона погрузили 91 т угля. Во втором вагоне оказалось в раза больше. Сколько угля погрузили в каждый вагон?
Представьте в виде дроби выражение .
Контрольная работа №6 «Нахождение числа по его дроби».
Вариант 1.
Найдите значение выражения:
а) б) в) .
2. Решите уравнение .
Вспахали поля, что составило 210 га. Какова площадь всего поля?
Заасфальтировали 35% дороги, после чего осталось заасфальтировать еще 13 км. Какова длина всей дороги?
0,9 от 20% числа р равны 5,49. Найдите число р.
Вариант 2.
Найдите значение выражения:
а) б) в) .
Решите уравнение .
Заасфальтировали дороги, что составило 45 км. Какова длина всей дороги?
Вспахали 45% поля, после чего осталось вспахать еще 165 га. Какова площадь всего поля?
0,7 от 40% числа d равны 2,94. Найдите число d.
Контрольная работа №7: «Отношения и пропорции».
Вариант 1.
Решите уравнение: 1,3 : 3,9 = х : 0,6.
Для изготовления 8 одинаковых приборов требуется 12 кг цветных металлов. Сколько килограммов цветных металлов потребуется для изготовления 6 таких приборов?
Для перевозки груза потребовалось 14 автомашин грузоподъемностью 4,5 т. Сколько потребуется автомашин грузоподъемностью 7 т для перевозки.
Найдите значение выражения:
а) ; б)
Сначала цена товара понизилась на 15%, а потом его новая цена повысилась на 15%. Стал товар дешевле или дороже его первоначальной стоимости?
Вариант 2.
Решите уравнение: у : 4,2 = 3,4 : 5,1.
При изготовлении 9 одинаковых приборов потребовалось 300 г серебра. Сколько серебра потребуется для изготовления 6 таких приборов?
Для перевозки груза потребовалось 14 автомашин грузоподъемностью 4,5 т. Сколько потребуется автомашин грузоподъемностью 7 т для перевозки этого же груза?
Найдите значение выражения:
а) ; б)
Сначала цена товара повысилась на 12%, а через год новая цена понизилась на 12%. Стал товар дешевле или дороже первоначальной стоимости?
Контрольная работа №8 «Длина окружности и площадь круга»
Вариант 1.
Найдите значение выражения:
а) ; б) .
Какую длину имеет на карте отрезок, изображающий расстояние 85 км, если масштаб карты1 : 1000000?
На чертеже в одном и том же масштабе изображены два стержня. Первый на чертеже имеет длину 5,2 см, а второй 6,4 см. Какова длина первого стержня в действительности, если действительная длина второго стержня 0,96 м?
Найдите площадь круга, если длины окружности этого круга равны 24,8 см. (Число π ≈ 3,1).
Найдите длину окружности, если длина её радиуса 2,25 дм. (Число π ≈ 3,14).
Площадь земельного участка прямоугольной формы 6а. Найдите площадь прямоугольника, изображающего этот участок на плане масштаб которого 1 : 500.
Вариант 2.
Найдите значение выражения:
а) ; б) .
Какую длину имеет на карте отрезок, изображающий расстояние в 45 км, если масштаб карты1 : 1 000 000?
На чертеже изображён напильник с ручкой. Длина напильника на чертеже 4,2 см, а длина ручки 1,5 см. Какова длина ручки напильника в действительности, если длина напильника в действительности равна 25,2 см?
Найдите площадь круга, если длины
окружности этого круга равны 12,4 см. (Число π ≈ 3,1).Найдите длину окружности, если длина её радиуса 3,25 дм. (Число π ≈ 3,14).
Площадь земельного участка прямоугольной формы 6а. Найдите площадь этого прямоугольника в действительности, если чертёж выполнен в масштабе 1 : 5.
Контрольная работа №9: «Положительные и отрицательные числа»
Вариант 1.
Отметьте на координатной прямой точки А (3), В ( – 4), С ( – 4,5), D (5,5), Е ( – 3). Какие из отмеченных точек имеют противоположные координаты?
Отметьте на координатной прямой точку А ( – 6), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки В, С, D, Е, если В правее А на 20 клеток, С – середина отрезка АВ, точка D левее точки С на 5 клеток и Е правее точки D на 10 клеток. Найдите координаты точек В, С, D и Е.
Сравните числа:
а) – 1,5 и – 1,05; б) – 2,8 и 2,7; в) и .
Найдите значение выражения:
а) ; б) ; в) .
Сколько целых чисел расположено между числами – 26 и 105?
Вариант 2.
Отметьте на координатной прямой точки М (– 7 ), N ( 4 ), K ( 3,5 ), P (– 3,5 ) и S (– 1). Какие из отмеченных точек имеют противоположные координаты?
Отметьте на координатной прямой точку А ( 3 ), приняв за единичный отрезок длину двух клеток тетради. Отметьте на этой прямой точки M, N, K и Р, если М левее А на 18 клеток, N – середина отрезка АM, точка K левее точки N на 6 клеток, а Р правее точки N на 7 клеток. Найдите координаты точек M, N, K и Р.
Сравните числа:
а) 3,6 и – 3,7; б) – 8,3 и – 8,03; в) и .
Найдите значение выражения:
а) ; б) ; в) .
Сколько целых чисел расположено между числами – 157 и 44?
Контрольная работа №10 «Сложение и вычитание положительных и отрицательных чисел».
Вариант 1.
Выполните действия:
а) – 3,8 – 5,7; б) – 8,4 + 3,7; в) 3,9 – 8,4;
г) – 2,9 + 7,3; д) ; е) .
Найдите значение выражения ( – 3,7 – 2,4 ) – + 5,9.
Решите уравнение: а) х + 3,12 = – 5,43; б) .
Найдите расстояние между точками А (– 2,8) и В (3,7) на координатной прямой.
Напишите все целые значения n, если .
Вариант 2.
Выполните действия:
а) – 3,5 + 8,1; б) – 2,9 – 3,6; в) – 7,5 + 2,8;
г) 4,5 – 8,3; д) ; е) .
Найдите значение выражения – ( – 1,8 – 4,3 ) – 5,7.
Решите уравнение: а) 5,23 + х = – 7,24; б) .
Найдите расстояние между точками C (–4,7) и D (–0,8) на координатной прямой.
Напишите все целые значения y, если .
Вариант 3.
Выполните действия:
а) – 7,5 + 4,2; б) – 4,7 + 2,9; в) – 3,7 – 5,8;
г) 3,7 – 5,6; д) ; е) .
Найдите значение выражения ( 3,9 – 5,8 ) – + 1,1.
Решите уравнение: а) 4,31 – х = 5,18; б) .
Найдите расстояние между точками M (–7,1) и N (4,2) на координатной прямой.
Напишите все целые значения m, если .
Вариант 4.
Выполните действия:
а) – 7,4 – 2,9; б) – 4,1 + 2,8; в) 8,7 – 9,4;
г) – 3,7 + 5,6; д) ; е) .
Найдите значение выражения – ( – 3,9 – 2,2 ) – 5,3.
Решите уравнение: а) х – 3,22= – 8,19; б) .
Найдите расстояние между точками K (–0,2) и P (–3,1) на координатной прямой.
Напишите все целые значения z, если .
Контрольная работа №11 «Умножение и деление положительных и отрицательных чисел».
Вариант 1.
Выполните действия:
а) ; б) ; в) ; г)
Выполните действия:
Выразите числа и в виде приближенного значения десятичной дроби до сотых.
Найдите значение выражения: .
Найдите корни уравнения: .
Вариант 2.
Выполните действия:
а) ; б) ; в) ; г)
Выполните действия:
Выразите числа и в виде приближенного значения десятичной дроби до сотых.
Найдите значение выражения: .
Найдите корни уравнения: .
Контрольная работа №12 «Раскрытие скобок. Подобные слагаемые»
Вариант 1.
Раскройте скобки и найдите значение выражения:
23,6 + ( 14,5 – 30,1 ) – (6,8 – 1,9).
Упростите выражение: .
Решите уравнение: .
Купили 0,8 кг колбасы и 0,3 кг сыра. За всю покупку заплатили 3,28р. Известно, что 1 кг колбасы дешевле 1 кг сыра на 0,3 р. Сколько стоит 1 кг сыра?
При каких значениях, а верно: ?
Найдите значение выражения – 8n – (4n – 6k), если k – 2n = 11.
Найдите значение выражения предварительно его, упростив
– 4(8х – 9у) + 3(6х – 4у), если х = – 2,8, у = 0,9.
Найдите значение выражения, применив распределительное свойство умножения:
а) ; б) .
Вариант 2.
Раскройте скобки и найдите значение выражения:
17,8 – (11,7 + 14,8) – (3,5 – 12,6).
Упростите выражение:.
Решите уравнение:.
Купили 1,2 кг конфет и 0,8 кг печенья. За всю покупку заплатили 5,96 р. Известно, что 1 кг конфет дороже 1 кг печенья на 1,3 р. Сколько стоит 1 кг конфет?
При каких значениях m верно: ?
Найдите значение выражения 9х – (3х + 2у), если 3х – у=19.
Найдите значение выражения предварительно его, упростив
3(5m – 4n) – 4(3m – 2n), если m = – 0,2, n = 0,7.
Найдите значение выражения, применив распределительное свойство умножения:
а) ; б) .
Контрольная работа №13 «Решение уравнений»
Вариант 1.
Решите уравнение: 0,7 + 0,3 ( х + 2 ) = 0,4 ( х – 3 ).
В первом букете было в 4 раза меньше роз, чем во втором. Когда к первому букету добавили 15 роз, а ко второму 3 розы, то в обоих букетах роз стало поровну. Сколько роз было в каждом букете первоначально?
Сумма двух чисел равна 138. Найдите эти числа, если одного из них равны 80% другого.
При каких значениях х выражения будут равны?
Найдите два корня уравнения .
Вариант 2.
Решите уравнение: 0,5 ( х – 3 ) = 0,6 ( х + 4 ) – 2,6.
В первой корзине было в 3 раза больше ягод, чем во второй. Когда из первой корзины взяли 8 кг ягод, а во вторую добавили 14 кг ягод, то в корзинах ягод стало поровну. Сколько килограммов ягод было в каждой корзине первоначально?
Сумма двух чисел равна 48. Найдите эти числа, если 40% одного из них равны другого.
При каких значениях х выражения будут равны?
Найдите два корня уравнения: .
Контрольная работа №14 «Координаты на плоскости»
Вариант 1.
Отметьте на координатной плоскости точки А (–4;0),
В (2;6), С (–4;3), D (4;–1). Проведите луч АВ и отрезок СD. Найдите координаты точек пересечения луча АВ и отрезка СD.
Постройте угол, равный 100
. Отметьте внутри угла точку С. Проведите через точку С прямые параллельные сторонам угла.Постройте угол МАР, равный 35
, и отметьте на стороне АМ точку D. Проведите через точку D прямые, перпендикулярные сторонам угла МАР.Уменьшаемое равно а, вычитаемое равно в. Чему будет равен результат, если от уменьшаемого отнять разность этих чисел?
Придумать и построить фигуры на плоскости записать координаты построенных точек.
Вариант 2.
На координатной плоскости проведите прямую МN через точки М (–4; –2) и N (5;4) и отрезок КD, соединяющий точки
К (–9;4) и D (–6; –8). Найдите координаты точек пересечения отрезка КD и прямой МN.
Постройте угол, равный 140
. Отметьте внутри угла точку и проведите через неё прямые, параллельные сторонам угла.Постройте угол СМК, равный 45
. Отметьте на стороне МС точку А и проведите через неё прямые, перпендикулярные сторонам угла СМК.Делимое равно а, делитель равен в (а и в не равны нулю). Чему будет равно произведение делителя и частного этих чисел?
Придумать и построить фигуры на плоскости записать координаты построенных точек.
Итоговая контрольная работа № 15 6 класс.
Вариант 1
Часть I
1. Укажите верное утверждение:
А. 3 делитель 26; Б. 0 делитель 5;
В. 4 делитель 2; Г. 37 делитель 814.
2. Какое из данных чисел кратно 5?
А. 678 905; Б. 55 556; В. 458 907; Г. 6 7904 369.
3. Сократите дробь
А. 5; Б. В. Г. Сократить нельзя.
4. Выполните вычитание:
А. Б. В. Г.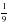 
5. Турист проходит в среднем км в час. Какое расстояние он пройдёт за ч?
Ответ:____________
6. Укажите в соответствии взаимно обратные числа.
1) 
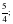2) 3) 4)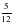 
А) 1,4; Б) 0,8; В) 2,4; Г) 1,5.
7. Найдите площадь круга, диаметр которого равен 8 см.
Ответ:___________
8. У какого из данных чисел наибольший модуль?
А. – 34,5; Б. 34,34; В. – 0,0997; Г. 0,769.
9. Раскройте скобки в выражении – (х + 4у – 3с)
А. – х + 4у – 3с; Б. х – 4у + 3с;
В. – х – 4у + 3с; Г. Другой ответ.
10. Решите уравнение 4,2х + 5 = – 7,6.
Ответ:______________
Часть II
1. (2 балла) Найдите значение выражения
2. (4 балла) Определите, при каком значении х значение выражения больше значения на 2.
3. (6 баллов) Найдите число а, если от а на 13 больше, чем 30% от а.
Вариант 2
Часть I
1. Укажите верное утверждение:
А. 33 кратно 11; Б. 17 кратно 0;
В. 45 кратно 2; Г. 565 кратно 15.
2. Сколько делителей у числа 18?
А. Три. Б. Пять. В. Шесть. Г. Другой ответ.
3. Сократите дробь
А. Б. В. Сократить нельзя. Г.
4. Выполните вычитание:
А. Б. В. Г.
5. Скорость течения реки км/ч. Какое расстояние пройдёт плот по течению реки за ч?
Ответ:____________
6. Укажите в соответствии взаимно обратные числа.
1) 2) 3) 4)
А. Б. В. Г.
7. Найдите площадь круга, радиус которого равен 5 см.
Ответ:__________
8. Какое из данных чисел наибольшее?
А. Б. В. Г.
9. Раскройте скобки в выражении – (2а – b + с)
А. – 2а – b – с. Б. – 2а – b + с.
В. –2а + b – с. Г. Другой ответ.
10. Решите уравнение – 0,25х + 0,8 = 1,3
Ответ:_____________
Часть II
1. (2 балла) Найдите значение выражения
2. (4 балла) Определите, при каком значении х значение выражения больше значения выражения на 1.
3. (6 баллов) Найдите число т, если от т равны 30% от числа т + 10.
Вариант 3
Часть I
1. Укажите верное утверждение:
А. 5 делитель 125; Б. 13 делитель 28;
В. 6 делитель 2; Г. 0 делитель 7.
2. Какое из данных чисел кратно 3?
А. 645 106; Б. 37 272; В. 58 127; Г. 7 295 224.
3. Сократите дробь
А. ; Б. 4 В. Г. Сократить нельзя.
4. Выполните вычитание:
А. Б. В. 4 Г.
5. Велосипедист проезжает в среднем км в час. Какое расстояние он проедет за ч?
Ответ:____________
6. Укажите в соответствии взаимно обратные числа.
1) 5; 2) 3) 4)
А) 1,6; Б) 1,3; В) 3,2; Г) 0,2.
7. Найдите площадь круга, диаметр которого равен 16 см.
Ответ:___________
8. У какого из данных чисел наименьший модуль?
А. – 0,1; Б. – 12,37; В. – 0,0345; Г. 1,23.
9. Раскройте скобки в выражении – (с + 7b – а)
А. – с – 7b + а; Б. – с + 7b + а;
В. – с + 7b – а; Г. Другой ответ.
10. Решите уравнение 0,7х – 1,82 = 0,8х + 3,46
Ответ:______________
Часть II
1. (2 балла) Найдите значение выражения
2. (4 балла) Определите, при каком значении х значение выражения больше значения на 3.
3. (6 баллов) Найдите число р, если от р на 9 больше, чем 40% от р.
Вариант 4
Часть I
1. Укажите верное утверждение:
А. 13 кратно 10; Б. 12 кратно 36;
В. 46 кратно 23; Г. 5 кратно 0.
2. Сколько делителей у числа 18?
А. Шесть. Б. Пять. В. Семь. Г. Другой ответ.
3. Сократите дробь
А. Б. В. Сократить нельзя. Г.
4. Выполните вычитание:
А. Б. В. Г.
5. Скорость течения реки км/ч. Какое расстояние пройдёт плот по течению реки за ч?
Ответ:____________
6. Укажите в соответствии взаимно обратные числа.
1) 2) 3) 4)
А. Б. В. Г.
7. Найдите площадь круга, радиус которого равен 6 см.
Ответ:__________
8. Какое из данных чисел наибольшее?
А. Б. В. Г.
9. Раскройте скобки в выражении – (3х + 2у – с)
А. – 3х + 2у – с; Б. – 3х + 2у + с;
В. – 3х – 2у + с; Г. Другой ответ.
10. Решите уравнение 3,6 + 2х = 5х + 1,2
Ответ:_____________
Часть II
1. (2 балла) Найдите значение выражения
2. (4 балла) Определите, при каком значении х значение выражения больше значения выражения на 1.
3. (6 баллов) Найдите число а, если от а на 2 больше, чем 20% от а.
Ответы.
Часть 1.
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вариант 1 | Г | А | Б | Б | 5 км | 1→Б; 2→Г 3→А; 4→В | 50,24 см2 | А | В | х = – 3 |
| Вариант 2 | А | В | А | Г | км | 1→В; 2→А; 3→Г; 4→Б | 78,5 см2 | Г | В | х = – 2 |
| Вариант 3 | А | Б | В | Б | км | 1→Г; 2→Б; 3→А; 4→В | 200,96 см2 | В | А | х = – 52,8 |
| Вариант 4 | В | А | Г | Б | км | 1→Б; 2→Г; 3→В; 4→А | 113,04 см2 | А | В | х = 0,8 |
Часть II
| | 1 | 2 | 3 |
| Вариант 1 | | х =23 | а =90 |
| Вариант 2 | | х = – 15 | т = 40 |
| Вариант 3 | 2,2 | х = 80 | р = 40 |
| Вариант 4 | | х = – 13 | а = 90 |
Для оценивания результатов выполнения работ учащимися применяются два количественных показателя: традиционная отметка («2», «3», «4» и «5») и рейтинг: от 0 до 22 баллов, назначение рейтинга – расширение диапазона традиционной отметки.
Рейтинг формируется путём подсчёта общего количества баллов, полученных учащимися за выполнение первой и второй частей работы. За каждое верно решённое задание первой части учащемуся начисляется 1 балл. Во второй части работы около каждого задания указано количество баллов, которое засчитываются в рейтинговую оценку ученика при верном выполнении этого задания и характеризуют относительную сложность этого задания в работе.
Критерии оценивания
| Отметка | Количество баллов |
| «3» | 5 – 8 |
| «4» | 9 – 15 |
| «5» | 16 – 22 |
| № урока | Вид контроля | Тема | Источник | Страница |
| 27 | Тест | Сокращение дробей. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 14 – 15 |
| 34 | Тест | Сравнение, сложение и вычитание дробей с разными знаменателями. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 18 – 19 |
| 49 | Тест | Умножение дробей. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 20 – 21 |
| 64 | Тест | Умножение и деление обыкновенных дробей. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 26 – 27 |
| 115 | Тест | Сложение отрицательных чисел. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 44 – 45 |
| 122 | Тест | Умножение положительных и отрицательных чисел. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 54 – 55 |
| 125 | Тест | Деление положительных и отрицательных чисел. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 56 – 57 |
| 144 | Тест | Решение уравнений. | Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с. | 64 – 65 |
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКИХ СРЕДСТВ ОБУЧЕНИЯ
Основная литература
Контрольно – измерительные материалы. Математика 5 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2014. – 96 с.
Контрольно – измерительные материалы. Математика 6 класс/ Сост. Л. П. Попова. – 3-е изд., перераб. – М.: ВАКО, 2013. – 96 с.
Учебник: Математика. 5 класс/ Н. Я. Виленкин, В.И.Жохов, А.С.Чесноков, С. И. Шварцбурд – М.: Мнемозина, 2008.
Учебник: Математика. 6 класс: учеб. для общеобразоват. учрежд. / Виленкин Н. Я., В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд/. - М.: Мнемозина, 2009.
Оборудование
Дидактические материалы.
Технические средства обучения: мультимедийный проектор.
Аудиторная доска с магнитной поверхностью.
Комплект инструментов классных: линейка, транспортир, циркуль.
Полезное для учителя
Распродажа видеоуроков!
1500 руб.
2500 руб.
1500 руб.
2500 руб.
1440 руб.
2400 руб.
1240 руб.
2070 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства