Рабочая программа «Математика» 5 - 6 классы

Муниципальное бюджетное общеобразовательное учреждение

«Лицей № 17»

Рабочая программа

«Математика»

5 - 6 классы

Берёзовский 2014

Муниципальное бюджетное общеобразовательное учреждение

«Лицей № 17»

Рабочая программа

«Математика»

5 - 6 классы

	Составитель:
	Петрова В.А., учитель математики МБОУ «Лицей № 17»

Программа обсуждена Программа утверждена на

на заседании методического педагогическом совете

объединения протокол № __от ______2014г. протокол № ___ от ______2014г. Директор лицея______Л.И. Ляскина Руководитель МО ______В.А. Петрова

Березовский 2014

Оглавление

Пояснительная записка 4

Содержание курса обучения 5 класса 7

Требования к уровню подготовки учащихся к окончанию 5 класса 8

Тематическое планирование учебного материала курса математики. 5 класс. 11

Содержание курса обучения 6 класса 14

Требования к уровню подготовки учащихся к окончанию 6 класса 14

Тематическое планирование учебного материала курса математики. 6 класс. 18

Контрольные работы за курс математики 5 класса 20

Контрольные работы за курс математики 6 класса 35

Литература для обучающихся 52

Литература для педагога 53

Пояснительная записка

Рабочая программа «Математика» для учащихся 5-6 классов составлена на основе Федерального государственного образовательного стандарта основного общего образования по математике, федерального перечня учебников, рекомендованных или допущенных к использованию в образовательном процессе в образовательных учреждениях, базисного учебного плана, авторского тематического планирования учебного материала и требований к результатам общего образования, представленных в Федеральном образовательном государственном стандарте общего образования, с учетом преемственности с примерными программами для начального общего образования.

Данная рабочая программа ориентирована на использование учебника И.И. Зубаревой, А.Г. Мордковича (М.: Мнемозина).

Математическое образование в основной школе складыва­ется из следующих содержательных компонентов: арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистикии логики. В своей совокупности они отража­ют богатый опыт обучения математике в нашей стране, учи­тывают современные тенденции отечественной и зарубеж­ной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно – емком и практически значимом материале.

Изучение математики в 5 – 6 классах направлено на достижение следующих целей:

• овладение системой математических зна­ний и умений, необходимых для примене­ния в практической деятельности, изучения смежных дисциплин, продолжения образо­вания;

• интеллектуальное развитие, формирование качеств личности, необходимых челове­ку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логи­ческого мышления, элементов алгоритми­ческой культуры, пространственных пред­ставлений, способности к преодолению трудностей;

• формирование представлений об идеях и ме­тодах математики как универсального языка науки и техники, средства моделирования яв­лений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, формирование понимания значи­мости математики для научно-технического прогресса.

Задачи обучения:

• приобретение математических знаний и уме­ний;

• овладение обобщенными способами мысли­тельной, творческой деятельности;

• освоение компетенций (учебно-познаватель­ной, коммуникативной, рефлексивной, лич­ностного саморазвития, информационно-тех­нологической, ценностно-смысловой).

• построение образовательного процесса с уче­том индивидуальных возрастных, психологи­ческих и физиологических особенностей об­учающихся.

Достижение вышеуказанных целей осуществ­ляется в процессе формирования следующих ком­петенций:

• учебно-познавательной (постановка цели и ор­ганизация ее достижения, умение пояснить свою цель; организация планирования, ана­лиза, рефлексии, самооценки своей учебно­познавательной деятельности; постановка вопросов к наблюдаемым фактам, поиск причины явлений, обозначение своего по­нимания или непонимания по отношению к изучаемой проблеме; постановка позна­вательной задачи и выдвижение гипотезы; выбор условий проведения наблюдения или опыта; выбор необходимого оборудования, владение измерительными навыками, работа с инструкциями; использование элементов ве­роятностных и статистических методов позна­ния; описание результатов, формулирование выводов; устное и письменное выступление о результатах своего исследования с использо­ванием компьютерных средств и технологий: текстовые и графические редакторы, презен­тации);

• коммуникативной (умение работать в груп­пе, готовность к речевому взаимодействию и взаимопониманию);

• рефлексивной (способность и готовность к са­мооценке, самоконтролю и самокоррекции);

• личностного саморазвития (овладение спо­собами деятельности в соответствии с соб­ственными интересами и возможностями, обеспечивающими физическое, духовное и интеллектуальное саморазвитие, эмоцио­нальную саморегуляцию и самоподдержку);

• информационно-технологической (умение ориентироваться, самостоятельно искать, анализировать, производить отбор, преобра­зовывать, сохранять, интерпретировать и осу­ществлять перенос информации и знаний при помощи реальных технических объектов и ин­формационных технологий);

• ценностно-смысловой (способность видеть и понимать окружающий мир, ориентировать­ся в нем, осознавать свою роль и предназна­чение, уметь выбирать целевые и смысловые установки для своих действий и поступков, принимать решения).

Образовательные технологии:

• информационно-коммуникационные;

• здоровьесберегающие;

• использования в обучении игровых методов: ролевых, деловых и других видов обучающих игр;

• проблемно-поисковый метод;

• элементы проектного метода обучения.

Признано, что основными технологиями развивающего обучения являются проблемно – поисковая, исследовательская технологии. Именно они позволяют создать такое образовательное пространство, в котором ученик является субъектом процесса обучения.

Применение этих технологий обеспечивается строгим соблюдением такого дидактического принципа, как принцип систематичности и последовательности изложения материала.

Основной организационной формой процесса обучения математики является урок. При реализации программы планируются различные виды уроков: урок изучения нового материала, урок-практикум по решению задач, уроки обобщения и систематизации учебного материала, комбинированные уроки, уроки исследования, игровые уроки.

Помимо контрольных работ система оценивания включает следующие виды контроля:

• фронтальный опрос;

• индивидуальная работа по карточкам;

• проверка домашней работы;

• самостоятельная работа;

• тестовая работа;

• математический диктант;

• практическая работа;

• контрольная работа;

• устный зачёт.

Учебное и учебно-практическое обеспечение

• Таблицы по математике для 5 классов;

• Таблицы по математике для 6 классов;

• таблицы выдающихся математиков;

• доска магнитная с координатной сеткой;

• комплект классных чертежных инструментов: линейка, транспортир, угольник (30°, 60°), угольник (45°, 45°), циркуль;

комплекты демонстрационных планиметри­ческих фигур и стереометрических тел.

Рабочая программа рассчитана на 420учебных часов согласно учебному плану МОУ «Лицей №17», из расчета 6 часов в неделю.

Согласно учебному плану (недельный) лицея для преподавания математики в 5 и 6 классах из Федерального компонента отводится 5ч и 1 ч из компонента образовательного учреждения, т.е. по 6 часов в неделю, всего 35 учебных недель, 210 ч в год в каждом из классов.

Содержание курса обучения 5 класса

Натуральные числа. Десятичная система счис­ления. Числовые и буквенные выражения. Пря­мая. Отрезок, сравнение отрезков, длина отрезка. Луч. Ломаная. Координатный луч. Прямоугольник. Округление чисел, прикидка результатов действий. Вычисления с многозначными числами, законы арифметических действий. Формулы. Уравнения. Упрощение выражений. Математическая модель, математический язык.

Обыкновенные дроби. Деление с остатком. Обыкновенные дроби. Отыскание части от целого и целого по его части. Основное свойство дроби. Правильные и неправильные дроби. Окружность и круг. Смешанные числа. Сложение и вычитание обыкновенных дробей и смешанных чисел. Умноже­ние и деление обыкновенной дроби на натуральное число.

Геометрические фигуры. Определение угла. Раз­вернутый угол. Сравнение и измерение углов. Бис­сектриса угла. Треугольник, площадь треугольника. Свойство углов треугольника. Расстояние между точками. Масштаб. Расстояние от точки до прямой. Перпендикулярные прямые. Серединный перпенди­куляр. Свойство биссектрисы угла.

Десятичные дроби. Понятие десятичной дроби, чтение и запись десятичных дробей. Умножение и деление десятичной дроби на 10, 100, 1000 и т. д. Перевод величин в другие единицы измерения. Сравнение, сложение и вычитание десятичных дро­бей. Умножение десятичных дробей. Степень чис­ла. Среднее арифметическое. Деление десятичной дроби на натуральное число, на десятичную дробь. Понятие процента. Задачи на проценты. Микро­калькулятор.

Геометрические тела. Прямоугольный параллеле­пипед, развертка прямоугольного параллелепипеда. Объем прямоугольного параллелепипеда.

Введение в вероятность. Достоверные, невозмож­ные и случайные события. Комбинаторные задачи.

Требования к уровню подготовки учащихся к окончанию 5 класса

В результате освоения курса математики 5 класса учащиеся должны овладеть следующими знаниями, умениями и навыками.

Личностным результатом изучения предмета яв­ляется формирование следующих умений и качеств:

• представление о математической науке как сфере человеческой деятельности, о ее зна­чимости в развитии цивилизации;

• креативность мышления, инициатива, наход­чивость, активность при решении математи­ческих задач.

Метапредметным результатом изучения курса яв­ляется формирование универсальных учебных дейст­вий (УУД).

Регулятивные УУД:

• самостоятельно обнаруживать и формулиро­вать учебную проблему, определять цель УД;

• выдвигать версии решения проблемы, осо­знавать (и интерпретировать в случае необ­ходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;

• составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);

• работая по плану, сверять свои действия с це­лью и при необходимости исправлять ошибки самостоятельно (в том числе и корректировать план);

• в диалоге с учителем совершенствовать само­стоятельно выбранные критерии оценки.

Познавательные УУД:

• проводить наблюдение и эксперимент под ру­ководством учителя;

• осуществлять расширенный поиск инфор­мации с использованием ресурсов библиотек и Интернета;

• создавать и преобразовывать модели и схемы для решения задач;

• осуществлять выбор наиболее эффектив­ных способов решения задач в зависимости от конкретных условий;

• анализировать, сравнивать, классифициро­вать и обобщать факты и явления;

• давать определения понятиям.

Коммуникативные УУД:

• самостоятельно организовывать учебное взаи­модействие в группе (определять общие цели, договариваться друг с другом и т. д.);

• в дискуссии уметь выдвинуть аргументы и контраргументы;

• учиться критично относиться к своему мне­нию, с достоинством признавать ошибочность своего мнения и корректировать его;

• понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргу­менты), факты (гипотезы, аксиомы, теории);

• уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Предметным результатом изучения курса являет­ся сформированность следующих умений.

Предметная область «Арифметика»

• Выполнять устно арифметические действия: сложение и вычитание двузначных чисел и де­сятичных дробей с двумя знаками, умножение однозначных чисел, однозначного на двузнач­ное число, деление на однозначное число, десятичной дроби с двумя знаками на одно­

значное число; сложение и вычитание обык­новенных дробей с однозначными числите­лями и знаменателями; умножение и деление обыкновенной дроби с однозначным числи­телем и знаменателем на натуральное число;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную — в виде десятичной, процен­ты — в виде дроби и дробь - в виде процентов;

• находить значения числовых выражений, со­держащих целые числа и десятичные дроби; обыкновенные дроби и смешанные числа;

• округлять целые и десятичные дроби, выпол­нять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; переводить одни единицы измерения в другие;

• решать текстовые задачи, включая задачи, связанные с дробями и процентами.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе с использованием при не­обходимости справочных материалов, кальку­лятора;

• устной прикидки и оценки результата вычис­лений; проверки результата вычисления с ис­пользованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальны­ми свойствами рассматриваемых процессов и явлений.

Предметная область «Алгебра»

• Переводить условия задачи на математиче­ский язык;

• использовать методы работы с простейшими математическими моделями;

• осуществлять в выражениях и формулах чис­ловые подстановки и выполнять соответству­ющие вычисления;

• изображать числа точками на координатном луче;

• определять координаты точки на координат­ном луче;

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выраже­ниях и формулах числовые подстановки и вы­полнять соответствующие вычисления;

• решать текстовые задачи алгебраическим ме­тодом.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составле­ния формул, выражающих зависимости между реальными величинами.

Предметная область «Геометрия»

• Пользоваться геометрическим языком для описания предметов окружающего мира;

• распознавать геометрические фигуры, разли­чать их взаимное расположение;

• изображать геометрические фигуры, распо­знавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;

• в простейших случаях строить развертки про­странственных тел;

• вычислять площади, периметры, объемы про­стейших геометрических фигур (тел) по фор­мулам.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных геометрических задач, связанных с нахождением изученных геоме­трических величин (используя при необходи­мости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Предметная область «Вероятность и статистика»

• Иметь представление о достоверном, невоз­можном и случайном событии;

• решать простейшие комбинаторные задачи перебором вариантов; методом построения дерева возможных вариантов.

Тематическое планирование учебного материала курса математики. 5 класс.

6 часов в неделю, всего 210

№ пара­графа/ пункта учебника	Тема		Коли­ чество часов
	Глава I. Натуральные числа (57 ч)
1	Десятичная система счисления		4
2	Числовые и буквенные выражения		4
3	Язык геометрических рисунков		4
4	Прямая. Отрезок. Луч		2
5	Сравнение отрезков. Длина отрезка		2
6	Ломаная		3
7	Координатный луч		2
	Контрольная работа № 1 «Сравнение натуральных чисел, прямая, отрезок, ломаная, координатный луч»		1
	Анализ контрольной работы		1
8	Округление натуральных чисел		4
9	Прикидка результата действия		3
10	Вычисления с многозначными чис­лами		5
	Контрольная работа № 2 «Округле­ние чисел, вычисления с многозначны­ми числами»		1
	Анализ контрольной работы		1
11	Прямоугольник		2
12	Формулы		2
13	Законы арифметических действий		2
14	Уравнения		2
15	Упрощение выражений		4
16	Математический язык		2
17	Математическая модель		2
	Контрольная работа № 3 «Уравне­ния, упрощение выражения»		1
	Анализ контрольной работы		1
	Зачёт №1 по теме «Натуральные числа»		2
Глава II. Обыкновенные дроби (43ч)
18	Деление с остатком		4
19	Обыкновенные дроби		2
20	Отыскание части от целого и целого по его части		4
21	Основное свойство дроби		5
22	Правильные и неправильные дроби. Смешанные числа		4
23	Окружность и круг		3
	Контрольная работа № 4 «Деление и дроби»		1
	Анализ контрольной работы
24	Сложение и вычитание обыкновен­ных дробей		6
25	Сложение и вычитание смешанных чисел		6
26	Умножение и деление обыкновен­ной дроби на натуральное число		4
	Контрольная работа № 5 «Арифме­тические действия с обыкновенными дробями»		1
	Анализ контрольной работы		1
	Зачёт №2 по теме «Обыкновенные дроби»		2
Глава III. Геометрические фигуры (31 ч)
27		Определение угла. Развернутый угол	2
28		Сравнение углов наложением	2
29		Измерение углов	2
30		Биссектриса угла	2
31		Треугольник	3
32		Площадь треугольника	3
33		Свойство углов треугольника	3
34		Расстояние между двумя точками. Масштаб	2
35		Расстояние от точки до прямой. Перпендикулярные прямые	2
36		Серединный перпендикуляр	3
37		Свойство биссектрисы угла	3
		Контрольная работа № 6 «Геоме­трические фигуры»	1
		Анализ контрольной работы	1
		Зачёт №3 по теме «Геометрические фигуры»	2
Глава IV. Десятичные дроби (46 ч)
38		Понятие десятичной дроби. Чтение и запись десятичных дробей	2
39		Умножение и деление десятичной дроби на 10, 100, 1000 и т. д.	3
40		Перевод величин в другие единицы измерения	3
41		Сравнение десятичных дробей	3
42		Сложение и вычитание десятичных дробей	5
		Контрольная работа № 7 «Сложение и вычитание десятичных дробей»	1
		Анализ контрольной работы	1
43		Умножение десятичных дробей	5
44		Степень числа	3
45		Среднее арифметическое. Деление десятичной дроби на натуральное число	3
46		Деление десятичной дроби на деся­тичную дробь	5
		Контрольная работа № 8 «Умноже­ние и деление десятичных дробей»	1
		Анализ контрольной работы	1
47		Понятие процента	3
48		Задачи на проценты	5
49		Микрокалькулятор	3
		Зачёт №4 по теме «Десятичные дроби»	2
Глава V. Геометрические тела (16 ч)
50		Прямоугольный параллелепипед	1
51		Развертка прямоугольного паралле­лепипеда	6
52		Объем прямоугольного параллеле­пипеда	5
		Контрольная работа № 9 «Геоме­трические тела»	1
		Анализ контрольной работы	1
		Зачёт №5 по теме «Геоме­трические тела»	2
Глава VI. Введение в вероятность (4 ч)
53		Достоверные, невозможные и слу­чайные события	2
54		Комбинаторные задачи	2
Повторение (13 ч)
		Арифметические действия с нату­ральными числами	1
		Решение арифметических задач	1
		Упрощение выражений	1
		Сложение и вычитание обыкновен­ных дробей и смешанных чисел	1
		Умножение и деление обыкновен­ных дробей на натуральное число	1
		Сравнение, сложение и вычитание десятичных дробей	1
		Умножение и деление десятичных дробей	1
		Арифметические действия с деся­тичными дробями	1
		Проценты	1
		Решение задач на проценты	1
		Итоговая контрольная работа № 10	1
		Анализ контрольной работы	1
		Итоговый урок	1
Всего			210

Содержание курса обучения 6 класса

Положительные и отрицательные числа. Коор­динаты. Поворот, центральная и осевая симме­трия. Параллельность прямых. Координатная пря­мая и координатная плоскость. Положительные и отрицательные числа. Модуль числа. Противо­положные числа. Сравнение чисел. Числовые вы­ражения, содержащие знаки «+» и «—». Алгебраи­ческая сумма и ее свойства. Правило вычисления значения алгебраической суммы двух чисел. Чис­ловые промежутки. Умножение и деление поло­жительных и отрицательных чисел, обыкновенных дробей. Правило умножения для комбинаторных задач.

Преобразование буквенных выражений. Рас­крытие скобок. Упрощение выражений. Решение уравнений. Решение задач с помощью уравнений. Основные задачи на дроби. Окружность. Длина окружности и площадь круга. Шар и сфера.

Делимость натуральных чисел. Делители и крат­ные. Делимость произведения, суммы и разности чисел. Признаки делимости на 2; 3; 4; 5; 9; 10; 25. Простые и составные числа. Разложение числа на простые множители. Наибольший общий дели­тель и наименьшее общее кратное. Взаимно простые числа. Признак делимости на произведение.

Математика вокруг нас. Отношение двух чисел. Диаграммы. Пропорциональность величин. Реше­ние задач с помощью пропорций. Знакомство с ве­роятностью и ее подсчетом.

Итоговое повторение.

Требования к уровню подготовки учащихся к окончанию 6 класса

В результате освоения курса математики 6 класса учащиеся должны овладеть следующими знаниями, умениями и навыками.

Личностным результатом изучения предмета яв­ляется формирование следующих умений и качеств:

• развитие умений ясно, точно и грамотно изла­гать свои мысли в устной и письменной речи, понимать смысл поставленной задачи;

• креативность мышления, общекультурное и интеллектуальное развитие, инициатива, находчивость, активность при решении ма­тематических задач;

• формирование готовности к саморазвитию, дальнейшему обучению;

• выстраивать конструкции (устные и пись­менные) с использованием математической терминологии и символики, выдвигать аргу­ментацию, выполнять перевод текстов с обы­денного языка на математический и обратно;

• стремление к самоконтролю процесса и ре­зультата деятельности;

• способность к эмоциональному восприятию математических понятий, логических рассу­ждений, способов решения задач, рассматри­ваемых проблем.

Метапредметным результатом изучения курса является формирование универсальных учебных действий (УУД).

Регулятивные УУД:

• самостоятельно обнаруживать и формулиро­вать учебную проблему, определять цель УД;

• выдвигать версии решения проблемы, осо­знавать (и интерпретировать в случае необ­ходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;

• составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);

• разрабатывать простейшие алгоритмы на ма­териале выполнения действий с натуральны­ми числами, обыкновенными и десятичными дробями, положительными и отрицательными числами;

• сверять, работая по плану, свои действия с це­лью и при необходимости исправлять ошибки самостоятельно (в том числе и корректировать план);

• совершенствовать в диалоге с учителем само­стоятельно выбранные критерии оценки.

Познавательные УУД:

• формировать представление о математической науке как сфере человеческой деятельности, о ее значимости в развитии цивилизации;

• проводить наблюдение и эксперимент под ру­ководством учителя;

• осуществлять расширенный поиск инфор­мации с использованием ресурсов библиотек и Интернета;

• определять возможные источники необхо­димых сведений, анализировать найденную информацию и оценивать ее достоверность;

• использовать компьютерные и коммуника­ционные технологии для достижения своих целей;

• создавать и преобразовывать модели и схемы для решения задач;

• осуществлять выбор наиболее эффектив­ных способов решения задач в зависимости от конкретных условий;

• анализировать, сравнивать, классифициро­вать и обобщать факты и явления;

• давать определения понятиям.

Коммуникативные УУД:

• самостоятельно организовывать учебное взаи­модействие в группе (определять общие цели, договариваться друг с другом и т. д.);

• в дискуссии уметь выдвинуть аргументы и контраргументы;

• учиться критично относиться к своему мне­нию, с достоинством признавать ошибочность своего мнения и корректировать его;

• понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты (гипотезы, аксиомы, тео­рии);

• уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Предметным результатом изучения курса являет- сформированность следующих умений.

Предметная область «Арифметика»

• Выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умно­жение однозначных чисел на двузначные, арифметические операции с обыкновенными дробями с однозначным знаменателем и чис­лителем;

• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случа­ях обыкновенную в виде десятичной, процен­ты — в виде дроби и дробь — в виде процентов;

• сравнивать рациональные числа, выполнять арифметические действия с рациональными числами, находить значения числовых выра­жений (целых и дробных), используя пись­менные вычисления;

• округлять целые числа и десятичные дроби, выполнять оценку числовых выражений;

• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; переводить одни единицы измерения в дру­гие;

• обладать знаниями о связи между группами величин (цена, количество, стоимость; ско­рость, время, путь; производительность, вре­мя работы, работа);

• решать текстовые задачи, включая задачи, связанные с отношениями и с пропорцио­нальностью величин, дробями и процентами.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных практических расчетных задач, в том числе с использованием при необхо­димости справочных материалов, калькулятора;

• устной прикидки и оценки результата вычис­лений; проверки результата вычисления с ис­пользованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальны­ми свойствами рассматриваемых процессов и явлений.

Предметная область «Элементы алгебры»

• Переводить условия задачи на математиче­ский язык;

• использовать методы работы с математиче­скими моделями;

• выполнять алгебраические преобразования це­лых выражений и применять их для решения учебных математических задач и задач, возни­кающих в смежных учебных дисциплинах;

• осуществлять в выражениях и формулах чис­ловые подстановки и выполнять соответству­ющие вычисления;

• определять координаты точки на координат­ной прямой;

• изображать числа точками на координатной прямой;

• определять координаты точки на плоскости, строить точки с заданными координатами;

• составлять буквенные выражения и формулы по условиям задач; осуществлять в выраже­ниях и формулах числовые подстановки и вы­полнять соответствующие вычисления;

• решать линейные уравнения и уравнения, сво­дящиеся к ним;

• решать текстовые задачи алгебраическим ме­тодом.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составле­ния формул, выражающих зависимости между реальными величинами.

Предметная область «Элементы геометрии»

• Пользоваться геометрическим языком для описания предметов окружающего мира;

• распознавать геометрические фигуры, разли­чать их взаимное расположение;

• изображать геометрические фигуры, распо­знавать на чертежах, моделях и в окружающей обстановке основные пространственные тела;

• в простейших случаях строить развертки про­странственных тел;

• вычислять площади, периметры, объемы про­стейших геометрических фигур (тел) по фор­мулам.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• решения несложных геометрических задач, связанных с нахождением изученных геоме­трических величин (используя при необходи­мости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).

Предметная область «Элементы вероятности и статистики»

• Воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей;

• решать удобным для себя способом (в том числе с помощью таблиц и графиков) комби­наторные задачи: на перестановку из трех эле­ментов, правило произведения, установление числа пар на множестве из 3—5 элементов;

• строить простейшие линейные, столбчатые и круговые диаграммы;

• производить подсчет вероятностей в простей­ших случаях;

• осуществлять перебор и подсчет числа вари­антов, в том числе в простейших прикладных задачах.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• сравнения и анализа разного рода информации, представленной в виде диаграмм, графиков.

Тематическое планирование учебного материала курса математики. 6 класс.

6 часов в неделю, всего 210

№ пара­графа/ пункта учебника	Тема	Коли­ чество часов
Глава I. Положительные и отрицательные числа. Координаты (84ч)
	Повторение курса 5 класса	4
1	Поворот и центральная симметрия	6
2	Положительные и отрицательные числа. Координатная прямая	5
3	Противоположные числа. Модуль числа	5
4	Сравнение чисел	5
	Контрольная работа №1 «Положительные и отрицательные числа. Координатная прямая. Модуль числа»	1
	Анализ контрольной работы	1
5	Параллельность прямых	3
6	Числовые выражения, содержащие знаки "+", "–"	5
7	Алгебраическая сумма и ее свойства	5
8	Правило вычисления значения алгебраической суммы двух чисел	6
9	Расстояние между точками координатной прямой	3
	Контрольная работа №2 «Алгебраическая сумма чисел»	1
	Анализ контрольной работы	1
10	Осевая симметрия	4
11	Числовые промежутки	3
12	Умножение и деление положительных и отрицательных чисел	5
13	Координаты	2
14	Координатная плоскость	6
15	Умножение и деление обыкновенных дробей	6
16	Правило умножения для комбинаторных задач	3
	Контрольная работа №3 «Координатная плоскость».	1
	Анализ контрольной работы	1
	Зачёт №1 «Положительные и отрицательные числа. Координаты»	2
Глава II. Преобразование буквенных выражений (45ч)
17	Раскрытие скобок	5
18	Упрощение выражений	6
19	Решение уравнений	6
20	Решение задач на составление уравнений	6
	Контрольная работа №4 «Решение уравнений».	1
	Анализ контрольной работы	1
21	Нахождение части от целого и целого по его части	5
22	Окружность. Длина окружности	4
23	Круг. Площадь круга.	4
24	Шар. Сфера	3
	Контрольная работа №5 «Нахождение части от целого и целого по его части».	1
	Анализ контрольной работы	1
	Зачёт №2 по теме «Преобразование буквенных выражений»	2
Глава III. Делимость натуральных чисел (38ч)
25	Делители и кратные	3
26	Делимость произведения	4
27	Делимость суммы и разности чисел	4
28	Признаки делимости на 2, 5, 10, 4 и 25	4
29	Признаки делимости на 3 и 9	4
	Контрольная работа №6 «Признаки делимости чисел».	1
	Анализ контрольной работы	1
30	Простые числа. Разложение числа на простые множители	4
31	Наибольший общий делитель	3
32	Взаимно простые числа. Признак делимости на произведение. Наименьшее общее кратное	6
	Контрольная работа №7 «НОД. НОК».	1
	Анализ контрольной работы	1
	Зачёт №3 по теме «Делимость натуральных чисел»	2
Глава IV. Математика вокруг нас (30ч)
33	Отношение двух чисел	3
34	Диаграммы	3
35	Пропорциональность величин	4
36	Решение задач с помощью пропорций	6
	Контрольная работа №8 «Пропорциональность величин».	1
	Анализ контрольной работы	1
37	Разные задачи	6
38	Первое знакомство с понятием «вероятность»	3
39	Первое знакомство с подсчетом вероятности	3
Повторение (13ч)
	Положительные и отрицательные числа	1
	Алгебраическая сумма чисел	1
	Умножение и деление положительных и отрицательных чисел	1
	Решение текстовых задач на применение всех арифметических действий с обыкновенными дробями.	1
	Упрощение выражений	1
	Решение уравнений	1
	Решение задач на составление уравнений	1
	Делимость натуральных чисел	1
	Проценты	1
	Решение задач на проценты	1
	Итоговая контрольная работа	1
	Анализ контрольной работы	1
	Итоговый урок	1
Всего		210

Контрольные работы за курс математики 5 класса

Контрольная работа № 1

Вариант 1

1. Для числа 12 738 026 запишите:

а) старший разряд;

б) какая цифра стоит в разряде десятков тысяч;

в) в каком разряде стоит цифра 8.

2. Запишите решение задачи в виде числового выражения и найдите его значение:

Данила купил 29 гвоздик, а Маша на 8 меньше. Сколько всего гвоздик они купили?

3. Выполните рисунок по описанию: Луч MN пересекает прямую AB в точке K.

4^О. 1 кг яблок стоит a р., а 1 кг груш – b р. Запишите в виде выражения стоимость двух килограммов яблок и четырех килограммов груш.

5^О. Скорость всадника х км/ч, а поезда – у км/ч. Запишите в виде выражения:

а) скорость сближения всадника и поезда при движении навстречу;

б) скорость удаления при движении в противоположные стороны;

в) скорость сближения, при условии, что поезд догоняет всадника;

г) скорость удаления, при условии, что поезд обогнал всадника.

Вариант 2

1. Для числа 203 574 320 запишите:

а) старший разряд;

б) какая цифра стоит в разряде десятков тысяч;

в) в каком разряде стоит цифра 5.

2. Запишите решение задачи в виде числового выражения и найдите его значение:

В одной коробке было 12 кг конфет, во второй – в 3 раза меньше. Сколько конфет было в двух коробках?

3. Выполните рисунок по описанию: Лучи MN и CD пересекаются в точке K.

4^О. 1 кг картофеля стоит x р., а 1 кг моркови – y р. Запишите в виде выражения: на столько 2 кг картофеля дешевле, чем 5 кг моркови.

5^О. Скорость движения мотоциклаa км/ч, а велосипеда – b км/ч. Запишите:

а) скорость сближения мотоциклаи велосипеда при движении навстречу;

б) скорость удаления при движении в противоположные стороны;

в) скорость сближения, при условии, что мотоциклдогоняет велосипед;

г) скорость удаления, при условии, что мотоциклобогнал велосипед.

Вариант 3

1. Для числа 75 489 956 008 121 запишите:

а) старший разряд;

б) какая цифра стоит в разряде десятков тысяч;

в) в каких разрядах стоит цифра 5.

2. Запишите решение задачи в виде числового выражения и найдите его значение:

У Коли было 5 орехов, у Миши на 3 больше, а у Саши – в 2 раза меньше, чем у Миши. Сколько всего орехов было у ребят?

3. Выполните рисунок по описанию: Прямые АВ и CD пересекаются в точке O. Луч MN пересекает прямые AB и CD в точках K и L.

4^О. 1 литр молока стоит a р., а 1 литр сока – b р. Запишите в виде выражения стоимость трех литров молока и двух литров сока.

5^О. Скорость пешехода х км/ч, а велосипедиста – у км/ч. Запишите в виде выражения:

а) скорость сближения пешехода и велосипедиста при движении навстречу;

б) скорость удаления при движении в противоположные стороны;

в) скорость сближения, при условии, что велосипедист догоняет пешехода;

г) скорость удаления, при условии, что велосипедист обогнал пешехода.

Вариант 4

1. Для числа 6 355 670 881 320 запишите:

а) старший разряд;

б) какая цифра стоит в разряде десятков тысяч;

в) в каких разрядах стоит цифра 5.

2.Запишите решение задачи в виде числового выражения и найдите его значение:

В одной коробке было 10 кг конфет, во второй – в 2 раза меньше, а в третьей – на 3 кг меньше, чем во второй. Сколько конфет было в трех коробках?

3. Выполните рисунок по описанию: Лучи MN и CD пересекаются в точке K. Прямая AB пересекает лучи MN и CD в точках A и B.

4^О. 1 кг творога стоит x р., а 1 кг масла – y р. Запишите в виде выражения: на столько 3 кг масла дороже, чем 2 кг творога.

5^О. Скорость движения автомобиляa км/ч, а велосипеда – b км/ч. Запишите в виде выражения:

а) скорость сближения автомобиля и велосипеда при движении навстречу;

б) скорость удаления при движении в противоположные стороны;

в) скорость сближения, при условии, что автомобиль догоняет велосипед;

г) скорость удаления, при условии, что автомобиль обогнал велосипед.

Контрольная работа № 2

Вариант 1

1. Округлите до тысяч:

а) 75 860; б) 124 320.

2. Не выполняя вычислений, определите старший разряд суммы, разности произведения и частного чисел: 644 и 28.

3. Вычислите: (12 148 + 305  12) : 52.

4^О. За какое время при движении против течения реки теплоход пройдет 180 км, если его собственная скорость 16 км/ч, а скорость течения – 1 км/ч?

5^О. Один маляр за 6 часов окрашивает 72 м², а второму для этого требуется на 2 часа больше. Какую площадь они могут окрасить за 5 часов, при совместной работе?

Вариант 2

1. Округлите до сотен тысяч:

а) 1 599 300; б) 853 000.

2. Не выполняя вычислений определите старший разряд суммы, разности, произведения и частного чисел: 182 и 26.

3. Вычислите: (1860 –  1010 : 5)  12.

4^О. Двигаясь по течению реки, за 4 часа самоходная баржа прошла 48 км. Определите собственную скорость баржи, если скорость течения – 2 км/ч.

5^О. За 8 часов токарь может выточить 24 детали, а его ученик в три раза меньше. Какое количество деталей они могут выточить за 5 часов, работая одновременно?

Вариант 3

1. Округлите до сотен:

а) 94 520; б) 1 790.

2. Не выполняя вычислений определите старший разряд суммы, разности, произведения и частного чисел: 110 552 и 2 126.

2. Вычислите: (5981 –  270 108 : 54)  14.

4^О. За какое время при движении по течению реки лодка пройдет 28 км, если её собственная скорость 6 км/ч, а скорость течения – 1 км/ч?

5^О. Одна бригада за 5 дней убирает урожай с 60 га, а второй для этого требуется на 1 день больше. С какой площади смогут убрать урожай эти бригады за 4 дня, при совместной работе?

Вариант 4

1. Округлите до десятков тысяч:

а) 155 780; б) 230 490.

2. Определите старший разряд суммы, разности, произведения и частного чисел: 28 640 и 5 728.

3. Вычислите: (89 142 + 507  14) : 48.

4^О. Двигаясь против течения реки, за 3 часа катер прошел 60 км. Определите собственную скорость катера, если скорость течения – 2 км/ч.

5^О. За 4 часа мастер может выложить плиткой 16 м², а его ученик в два раза меньше. Какую площадь они могут выложить плиткой за 7 часов, работая одновременно?

Контрольная работа № 3

Вариант 1

1. Упростите выражение и найдите его значение при х = 2

3х + 15х – 8.

2. Решите уравнение: 7y– 2y= 35.

3. Площадь прямоугольника 72 см², а одна из его сторон равна 9 см. Найдите вторую сторону и периметр прямоугольника.

4^О. Для приготовления смеси взяли чай двух сортов: 3 кг чая первого сорта по 220 р. за 1 кг и 7 кг чая второго сорта. Найдите цену чая второго сорта, если цена получившейся смеси – 171 р. за 1 кг.

5^О. По течению катер двигается со скоростью y км/ч, а против течения на 2 км/ч медленнее. Запишите на математическом языке:

а) скорость катера при движении против течения;

б) расстояние, пройденное катером за 6 ч движения по течению, больше расстояния, пройденного им за 3 часа против течения на 78 км.

Вариант 2

1. Упростите выражение и найдите его значение при у = 5

25у + 2у – 7.

2. Решите уравнение: 8х + 4х = 24.

3. Площадь прямоугольника 48 см², а одна из его сторон равна 6 см. Найдите вторую сторону и периметр прямоугольника.

4^О. Для составления смеси взяли 6 кг карамели по 70 р. за 1 кг и 4 кг шоколадных конфет. Найдите цену шоколадных конфет, если цена получившейся смеси – 78 р. за 1 кг.

5^О. По проселочной дороге велосипедист едет со скоростью x км/ч, а по шоссе в 3 раза быстрее. Запишите на математическом языке:

а) скорость велосипедиста на шоссе;

б) за 3 ч езды по шоссе велосипедист проехал на 35 км больше, чем за 2 ч по проселочной дороге.

Вариант 3

1. Упростите выражение и найдите его значение при у = 5

32x+ 2x –7x – 7.

2. Решите уравнение: 18y – 5y + 2y= 45.

3. Периметр прямоугольника 56 см, а одна из его сторон равна 7 см. Найдите площадь прямоугольника.

4^О. Для приготовления напитка смешали персиковый сок с яблочным соком: 5 л персикового сока по 17 р. за 1 л и 3 л яблочного сока. Найдите цену яблочного сока, если цена получившегося напитка – 15 р. 50 к. за 1 л.

5^О. Против течения теплоход двигается со скоростью v км/ч, а по течению на 4 км/ч быстрее. Запишите на математическом языке:

а) скорость теплохода при движении по течению;

б) расстояние, пройденное теплоходом за 5 ч движения по течению, больше расстояния, пройденного им за 2 часа против течения на 94 км.

Вариант 4

1. Упростите выражение и найдите его значение при y= 7

13y + 9y – 7y – 5.

2. Решите уравнение: 17х – 12х + 6x= 55.

3. Периметр прямоугольника 72 см, а одна из его сторон равна 9 см. Найдите площадь прямоугольника.

4^О. Для приготовления кофейного напитка смешали кофе двух сортов: 2 кг кофе «арабика» по 65 р. за 1 кг и 6 кг кофе «мокко». Найдите цену кофе «мокко», если цена получившейся смеси – 55 р. 25 к. за 1 кг.

5^О. По грунтовой дороге автомобиль едет со скоростью у км/ч, а по шоссе в 5 раз быстрее. Запишите на математическом языке:

а) скорость автомобиля на шоссе;

б) за 4 ч езды по шоссе автомобиль проехал на 135 км больше, чем за 2 ч по грунтовой дороге.

Контрольная работа № 4

Вариант 1

1. Представьте данную дробь в виде дроби со знаменателем 6: а) 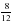; б) .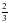

2. Девочка прочитала 25 страниц, что составило 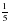книги. Сколько страниц в книге?.

3. Площадь тепличного хозяйства, 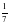которой занята под огурцы, составляет 140 а. Найдите площадь, занятую огурцами

4^О. Сколько километров пройдет катер за 5 часов, двигаясь по течению реки, скорость течения которой 1200 м/ч и это составляет 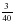собственной скорости катера?

5^О. Две окружности имеют общий центр. Радиус одной окружности – 4 см, а радиус второй окружности составляет 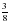диаметра первой. Начертите эти окружности.

Вариант 2

1. Представьте данную дробь в виде дроби со знаменателем 8: а) 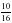; б) .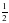

2. В книге 352 страницы. Мальчик прочитал 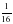книги. Сколько страниц прочитал мальчик?

3. Капустой занято 30 м², что составляет 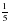площади всего огорода. Найдите площадь огорода.

4^О. Сколько километров пройдет моторная лодка за 4 часа, двигаясь против течения реки, если ее собственная скорость 22 км/ч, а скорость течения составляет 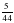собственной скорости катера?

5^О. Две окружности имеют общий центр. Радиус одной окружности – 4 см, и это составляет 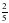диаметра второй окружности. Начертите эти окружности.

Вариант 3

1. Представьте данную дробь в виде дроби со знаменателем 15: а) 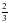; б) .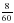

2. Площадь тепличного хозяйства, 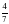которой занята под помидоры, составляет 140 а. Найдите площадь, занятую помидорами.

3. Девочка прочитала 105 страниц, что составило 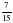книги. Сколько страниц в книге?

4^О. Сколько километров пройдет теплоход за 5 часов, двигаясь по течению реки, скорость течения которой 1500 м/ч и это составляет 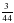собственной скорости теплохода?

5^О. Две окружности имеют общий центр. Радиус одной окружности – 6 см, а радиус второй окружности составляет 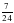диаметра первой. Начертите эти окружности.

Вариант 4

1.Представьте данную дробь в виде дроби со знаменателем 12: а) 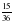; б) .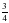

2. Картофелем занято 360 м², что составляет 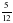всей площади огорода. Найдите площадь огорода.

3. В книге 352 страницы. Мальчик прочитал 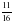книги. Сколько страниц прочитал мальчик?

4^О. Сколько километров пройдет теплоход за 6 часов, двигаясь против течения реки, если его собственная скорость 21 км/ч, а скорость течения составляет 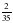собственной скорости катера?

5^О. Две окружности имеют общий центр. Радиус одной окружности – 5 см, и это составляет 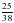диаметра второй окружности. Начертите эти окружности.

Контрольная работа №5

Вариант 1

1. Вычислите:

а) 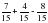; б) + – .

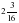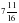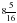2. Выполните действия:

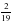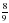а)  5; б) : 3.

3^О. Партия обуви, приобретенная предпринимателем, была продана за 3 дня. В первый день было продано 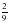числа всех пар обуви, во второй – 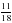. Какая часть обуви была продана в третий день?

4^О. За 3 часа из бассейна через одну трубу выливается 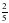, а через другую – 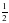всей воды. Какая часть воды выльется из бассейна за 1 час, если открыть обе трубы одновременно?

Вариант 2

1. Вычислите:

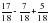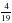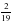а) ; б) 3 – 1 + 5.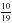

2. Выполните действия:

а) 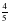: 7; б) 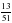 3.

3^О. За первую неделю бригада выполнила 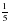всей работы по строительству дома, а за вторую – 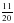всей работы. Какую часть работы осталось выполнить бригаде?

4^О. Один экскаватор за день работы выкапывает 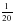часть котлована, а второй – 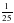. Какую часть котлована выкопают экскаваторы за 4 дня, работая одновременно?

Вариант 3

1. Вычислите:

а) 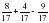; б) – + .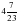

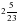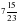2. Выполните действия:

а)  4; г) : 5.

3^О. На садовом участке были выращены огурцы, кабачки и тыквы. Масса огурцов составила , а масса кабачков – массы собранных овощей. Какую часть массы собранных овощей составили тыквы?

4^О. Миша за 3 часа может вскопать 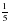площади огорода, а его отец за это же время огорода. Какую часть огорода могут вскопать Миша вместе с отцом за 1 час при одновременной работе?

Вариант 4

1. Вычислите:

а) ; б) 1 + 5 – 6 .

2. Выполните действия:

а) : 5; б)  8.

3^О. За первую минуту спортсмен пробежал , а за вторую – дистанции. Какую часть дистанции ему осталось пробежать?

4^О. Для двух котельных был сделан запас угля. Одна котельная в течение месяца расходует , а вторая – запаса угля. Какую часть угля израсходуют обе котельные за 4 месяца?

Контрольная работа № 6

Вариант 1

1. Начертите угол ABC равный 75. Отметьте внутри угла точку О и проведите через нее прямую, перпендикулярную стороне BC.

2. В треугольнике ABCА составляет 54, а C на 15 меньше. Найдите B треугольника ABC.

3^О. Вычислите: 201  15 – 7042 : 14.

4^О. В двух мешках было 75 кг крупы. После того как из первого мешка продали 12 кг, а из второго 18 кг, в первом мешке крупы оказалось в 2 раза больше, чем во втором. Сколько килограммов крупы было в каждом мешке первоначально?

Вариант 2

1. Начертите угол MNK равный 54. Отметьте внутри угла точку О и проведите через нее прямую, перпендикулярную стороне NM.

2. В треугольнике ABCА составляет 35, а B на 17 больше. Найдите C треугольника ABC.

3^О. Вычислите: 24 032 : 8 + 108  23.

4^О. В двух цистернах было 30 т бензина. После того как из каждой цистерны продали по 6 т, в первой цистерне оказалось в два раза больше бензина, чем во второй. Сколько тонн бензина было в каждой цистерне первоначально?

Вариант 3

1. Начертите угол MNK равный 54. Отметьте внутри угла точку О и проведите через нее прямые, перпендикулярные сторонам угла MNK.

2. В треугольнике ABCB составляет 14, а C в 3 раза больше. Найдите A треугольника ABC.

3^О. Вычислите: 637 637 : 91 – 207  12.

4^О. В трех бидонах 80 л молока. После того, как из одного бидона отлили 8 л, а из другого 12 л, в каждом из них оказалось молока в 2 раза меньше, чем в третьем бидоне. Сколько молока было в каждом бидоне первоначально?

Вариант 4

1. Начертите угол ABC равный 75. Отметьте внутри угла точку О и проведите через нее прямые, перпендикулярные сторонам угла ABC.

2. В треугольнике ABCА составляет 78, а B в 3 раза меньше. Найдите C треугольника ABC.

3^О. Вычислите: 145 261 : 29 – 103  47.

4^О. В три овощные магазина завезли 1600 кг картофеля. После того, как в первом магазине продали 200 кг, а во втором и третьем по 100 кг картофеля, в третьем магазине его осталось в 2 раза больше, чем в каждом из первых двух. Сколько кг картофеля было в каждом магазине первоначально?

Контрольная работа № 7

Вариант 1

1. Вычислите: а) 5,7 + 2,34; б) 1,2 – 0,83.

2. а) Выразите в метрах: 15 дм; 3,4 см; 7 мм.

б) Выразите в килограммах: 940 г; 7,2 т.

3. Длины сторон прямоугольника: 1,2 дм и 25 см. Выразите их в метрах и найдите периметр прямоугольника.

4^О. Мальчик поймал трех рыб. Масса первой рыбы – 0,375 кг, масса второй на 20 г меньше, а масса третьей на 0,11 кг больше массы первой рыбы. Найдите массу трех рыб.

5^О. Составьте выражение для длины ломаной ABCD, если AB = a, BC на 8,45 см меньше AB, а CD на 1,27 дм больше AB и упростите его.

Вариант 2

1. Вычислите: а) 6,83 + 15,3; б) 8,9 – 5,42.

2. а) Выразите в метрах: 3,2 дм; 543 см; 5 мм.

б) Выразите в килограммах: 56 г; 2,7 т.

3. Длины сторон прямоугольника: 3,8 дм и 54 см. Выразите их в метрах и найдите периметр прямоугольника.

4^О. Яблоко, груша и апельсин имеют массу 0,85 кг. Масса апельсина – 360 г, а груша на 0,158 кг легче. Найдите массу яблока.

5^О. Составьте выражение для длины ломаной ABCD, если AB = х, BC на 12,71 см меньше AB, а CD на 2,85 дм больше AB и упростите его.

Вариант 3

1. Вычислите: а) 15,7 + 2,341; б) 17,3 – 8,562.

2. а) Выразите в метрах: 5 дм; 2,54 см; 0,57 мм.

б) Выразите в килограммах: 0,32 г; 6,4 т.

3. Длины сторон треугольника: 2,5 дм, 30 см, 120 мм. Выразите их в метрах и найдите периметр треугольника.

4^О. Масса трех искусственных спутников 1,751 т. Масса первого спутника 6,6 ц, масса второго – на 73 кг больше. Найдите массу третьего спутника.

5^О. Составьте выражение для длины ломаной ABCD, если AB = у, BC на 7,35 см меньше AB, а CD на 5,12 дм больше AB и упростите его.

Вариант 4

1. Вычислите: а) 1,683 + 12,9; б) 15,2 – 6,587.

2. а) Выразите в метрах: 3,2 дм; 36,8 см; 0,08 мм.

б) Выразите в килограммах: 0,32 г; 6,4 т.

3. Длины сторон треугольника: 5,1 дм, 29 см, 340 мм. Выразите их в метрах и найдите периметр треугольника.

4^О. Слон, тигр и зубр вместе имеют массу 6,98 т. Масса слона 5,9 т, а тигр на 55,2 ц легче. Определите массу зубра (в кг).

5^О. Составьте выражение для длины ломаной ABCD, если AB = х, BC на 2,93 см меньше AB, а CD на 4,31 дм больше AB и упростите его.

Контрольная работа № 8

Вариант 1

1. Вычислите: а) 8,3  6; б) 2,06  1,5; в) 9,76 : 3,2.

2. Найдите среднее арифметическое чисел: 4,2; 4,1; 4,1; 4,3; 3,9.

3^О. За 400 г сыра и 1,2 кг колбасы заплатили 126 р. 80 к. Какова цена1 кг колбасы, если 1 кг сыра стоит 95 р?

4^О. На двух складах было 210,2 т картофеля. После того, как с первого склада было продано 24,5 т, а со второго 10,8 т, на первом складе картофеля оказалось в 2 раза больше, чем на втором. Сколько тонн картофеля было на каждом складе первоначально?

Вариант 2

1. Вычислите: а) 3,4  5; б) 3,08  6,7; в) 7,8 : 1,2.

2. Найдите среднее арифметическое чисел: 3,2; 4,5; 2,9; 3,1; 4,2.

3^О. За 80 см шелка и 2,5 м шерсти заплатили 336 р. 40 к. Какова цена 1 м шерсти, если 1 м шелка стоит 58 р.

4^О. В двух бидонах было 51 л молока. Когда из первого бидона отлили 16,2, а из второго 7,2 литра, то во втором бидоне молока оказалось в 4 раза больше, чем в первом. Сколько литров молока было в каждом бидоне первоначально?.

Вариант 3

1. Вычислите: а) 78,56  1,05; б) 46,508 : 1,51; в) 0,000135 : 2,7.

2. На соревнованиях по гимнастике двое судей оценили выступление спортсмена в 9,4 балла, трое в 9,5 балла и еще трое в 9,6 балла. Найдите средний балл спортсмена.

3^О. За 600 г масла и 1,4 кг творога заплатили 103 р. 80 к. Какова цена 1 кг творога, если 1 кг масла стоит 75 р?

4^О. В два магазина завезли 5,28 ц рисовой крупы. После того, как из первого магазина продали 1,3 ц, а из второго 2,54 ц крупы, то в первом магазине крупы осталось в 2 раза больше, чем во втором. Сколько центнеров крупы завезли в каждый магазин первоначально?

Вариант 4

1. Вычислите: а) 2,06  29,35; б) 51,456 : 1,28; в) 0,00245 : 3,5.

2. На соревнованиях по парному фигурному катанию трое судей выставили оценку 5,4 балла, двое по 5,3 балла, еще двое по 5,5 балла и один – 5,6 балла. Найдите средний балл спортсменов.

3^О. За 90 см ситца и 3,4 м полотна заплатили 148 р. 10 к. Какова цена 1 м полотна, если 1 м ситца стоит 21 р.?

4^О. В двух коробках 1,77 кг конфет. После того, как из первой коробки съели 0,56 кг, а из второй 0,91 кг конфет, то во второй коробке конфет осталось в 3 раза меньше, чем в первой. Сколько кг конфет было в каждой коробке первоначально?

Контрольная работа № 9

Вариант 1

1. Сметана содержит 20% жира. Сколько жира в 500 г сметаны?

2. В лесопарке посажено 15 кленов, что составляет 1% всех деревьев. Сколько деревьев в лесопарке?

3. Объем комнаты 45,36 м³. Найдите высоту потолка комнаты, если её площадь – 16,8 м².

4^О. С поля, засаженного капустой, в первый день было вывезено 58% урожая, а во второй – остальные 33,6 тонны. Сколько тонн капусты было вывезено с поля?

5^О. Найдите массу 1 м³ сплава, если слиток этого сплава, имеющий форму прямоугольного параллелепипеда с измерениями 2,9 дм, 15 см и 0,8 м имеет массу 281,88 кг.

Вариант 2

1. Сыр содержит 35% жира. Сколько жира в 400 г сыра?

2. Петрушкой засеяно 3 м², что составляет 1% площади огорода. Найдите площадь огорода.

3. Найдите высоту потолка спортивного зала, если его объем равен 5465,6 м³, а площадь пола – 854 м².

4^О. За первую неделю работы тротуарной плиткой было выложено 47% площади тротуара, а за вторую – остальные 561,8 м². Какова площадь тротуара?

5^О. Найдите массу 1 м³ кирпича, если один кирпич с измерениями 2 дм, 15 см и 0,1 м имеет массу 2,7 кг.

Вариант 3

1. В состав нержавеющей стали входит 1,8% хрома. Найдите массу хрома в слитке стали массой 5 кг.

2. Сливки содержат 21,2% жира. Сколько нужно сливок, чтобы получить 74,2 кг сливочного масла?

3. До какого уровня залита вода в бассейн, имеющий форму прямоугольного параллелепипеда со сторонами 10,5 м и 30 м, если ее объем равен 787,5 м³.

4^О. За первую неделю уборки урожая в саду было собрано 17% урожая яблок, а затем остальные 20,418 т. Сколько тонн яблок было собрано в саду?

5^О. Найдите массу 1 м³ сплава, если слиток этого сплава, имеющий форму прямоугольного параллелепипеда с измерениями 0,25 м, 8,5 см и 1,2 дм имеет массу 20,655 кг.

Вариант 4

1. Железная руда содержит 7,8% железа. Найдите массу железа в трех тоннах руды.

2. Сахарный тростник содержит 9% сахара. Сколько тростника потребуется, чтобы получить 144 кг сахара.

3. Найдите площадь поверхности воды в аквариуме, если 15 л воды заполняют его на 2,5 дм (1л = 1 дм³).

4^О. За первую неделю работы было отремонтировано 54% площади дорожного покрытия, а за вторую – остальные 667 м². Какова площадь отремонтированного дорожного покрытия?

5^О. Найдите массу 1 м³ бетонного блока для фундамента, если один блок с измерениями 1,5 м, 4 дм и 60 см имеет массу 900 кг.

Контрольная работа № 10

Вариант 1

1. Вычислите: (8,3 + 4,72)  (5,5 – 3,45).

2. Решите уравнение: 3,5x= 7,21.

3. В первом овощехранилище на 5,6 т картофеля больше, чем во втором, а в двух овощехранилищах вместе 80 т картофеля. Сколько тонн картофеля во втором овощехранилище?

4. Постройте с помощью транспортира угол BAC, равный 35, и отложите на луче AB отрезок AM длиной 6 см. Используя угольник, проведите через точку M прямую перпендикулярную AC и найдите площадь образовавшегося треугольника (в м²). Ответ округлите до сотых.

5. После того, как была продана четверть конфет, вес ящика с конфетами уменьшился на 24%. Определите массу пустого ящика, если масса ящика с конфетами – 60 кг.

Вариант 2

1. Вычислите: (7,6 + 5,85)  (10,9 – 4,86).

2. Решите уравнение: 6,5x = 26,52.

3. На первом складе на 7,6 т угля меньше, чем на втором, а на двух складах вместе 100 т угля. Сколько тонн угля на втором складе?

4. Постройте прямоугольник ABCD со сторонами AB = 5 см, AD = 8 см. Проведите луч AM, пересекающий BС в точке M так, чтобы угол BAM оказался равным 40. Выполните необходимые измерения и найдите площадь образовавшегося треугольника BAM (в м²). Ответ округлите до сотых.

5. После того, как была продана половина конфет, вес ящика с конфетами уменьшился на 45 %. Определите массу пустого ящика, если масса ящика с конфетами – 50 кг.

Вариант 3

1. Вычислите: (6,4 + 7,72) · (13,8 – 5,75).

2. Решите уравнение: 2,5y = 12,65.

3. В первой канистре на 4,8 л бензина больше, чем во второй, а в двух канистрах вместе 60 л бензина. Сколько литров бензина в первой канистре?

4. Постройте с помощью транспортира угол BAC, равный 55, и отложите на луче AС отрезок AM длиной 6 см. Используя угольник, проведите через точку M прямую перпендикулярную AC и найдите площадь образовавшегося треугольника (в м²). Ответ округлите до сотых.

5. После того, как была продана треть конфет, вес ящика с конфетами уменьшился на 32%. Зная, что полный ящик с конфетами весил 45 кг, определите, сколько весит пустой ящик.

Вариант 4

1. Вычислите: (4,1 + 7,95) · (7,4 – 5,32).

2. Решите уравнение: 5,5m = 38,72.

3. На первом складе на 9,8 т угля меньше, чем на втором, а на двух складах вместе 100 т угля. Сколько тонн угля на первом складе?

4. Постройте прямоугольник ABCD со сторонами AB = 4 см, AD = 6 см. Проведите луч AM, пересекающий СD в точке M так, чтобы угол DAM оказался равным 25. Выполните необходимые измерения и найдите площадь треугольника MAD(в м²). Ответ округлите до сотых.

5. После того, как одна пятая часть конфет была съедена, вес коробки с конфетами уменьшился на 15%. Зная, что полная коробка весила 0,4 кг, определите, сколько весит пустая коробка.

Контрольные работы за курс математики 6 класса

Контрольная работа №1

Вариант 1

1. Отметьте на координатной прямой числа:

2; –3,7; 3,5; –1,5.

Запишите:

а) наибольшее число;

б) наименьшее число;

в) число, имеющее наибольший модуль;

г) число, имеющее наименьший модуль.

2. Запишите число, противоположное данному:

а) 0,5; б) –7; в) 0.

3. Запишите x, если:

а) –х = 5; б) х = –; в) х = 0.

4^О. Сравните числа и их модули:

а) –5,8 и –0,1; б) –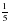 и –.

5^О. Вычислите:

а) –; б) – .

Вариант 2

1. Отметьте на координатной прямой числа:

–2; 2,5; 3; –4.

Запишите:

а) наибольшее число;

б) наименьшее число;

в) число, имеющее наибольший модуль;

г) число, имеющее наименьший модуль.

2. Запишите число, противоположное данному:

а) –10; б) 0; в) .

3. Запишите x, если:

а) х = ; б) х = 0; в) –х = –5,2.

4^О. Сравните числа и их модули:

а) –8,3 и –3,8; б) – и –.

5^О. Вычислите:

а) + ; б) – .

Вариант 3

1. Отметьте на координатной прямой числа:

–4,5; –1,8; 4; 3,2.

Запишите:

а) наибольшее число;

б) наименьшее число;

в) число, имеющее наибольший модуль;

г) число, имеющее наименьший модуль.

2. Запишите число, противоположное данному:

а) 0; б) –7,2; в) .

3. Запишите x, если:

а) х = 0; б) х = –; в) –х = 3.

4^О. Сравните числа и их модули:

а) –84,7 и 7,48; б) – и –.

5^О. Вычислите:

а) – ; б) – .

Вариант 4

1. Отметьте на координатной прямой числа:

4; –5; 1; –1,75.

Запишите:

а) наибольшее число;

б) наименьшее число;

в) число, имеющее наибольший модуль;

г) число, имеющее наименьший модуль.

2. Запишите число, противоположное данному:

а) –8; б) 0; в) 4,6.

3. Запишите x, если:

а) х = ; б) –х = –10; в) х = 0.

4^О. Сравните числа и их модули:

а) 3,48 и –84,3; б) – и –.

5^О. Вычислите:

а) – ; б) + .

Контрольная работа №2

Вариант 1

1. Найдите значение выражения:

а) –8 + 5;	в) –10 – 9;
б) 17 – 25;	г) –45 + 60.

2. Вычислите:

а) ; б) –; в) .

3. Найдите значение алгебраической суммы

–4,1 + (–8,3) – (–7,3) – (+1,9).

4^О. В магазин завезли 700 кг овощей, которые были проданы за 3 дня. В первый день было продано 40% овощей, во второй – 58% остатка. Определите массу овощей, проданных в третий день.

5^О. Предприниматель закупил партию сахара, которая была продана за три дня. В первый день было продано 36 ц, что составило 40% всей партии, во второй день – 35% остатка. Определите массу сахара, проданного в третий день.

Вариант 2

1. Найдите значение выражения:

а) –7 –15;	в) –16 + 20;
б) 23 – 40;	г) –9 + 3.

2. Вычислите:

а) ; б) ; в) .

3. Найдите значение алгебраической суммы

–8,9 + (+18) – (+1,1) – (–12).

4^О. Туристический теплоход был в пути три дня. В первый день он прошел 210 км, что составило 35% всего пути, а во второй – 40% оставшегося расстояния. Сколько километров прошел теплоход в третий день?

5^О. Предприятием по изготовлению пластиковой тары было изготовлено 5000 бутылок, которые были проданы за три дня. В первый день было продано 30% этого количества, а во второй – 70% остатка. Какое количество бутылок было продано в третий день?

Вариант 3

1. Найдите значение выражения:

а) 1,8 – 2,2;	в) –2,18 – 1,54;
б) –0,14 + 0,17;	г) –7,8 + 5,6.

2. Вычислите:

а) ; б) ; в) .

3. Найдите значение алгебраической суммы

–(–5,4) + (–2,8) + 4,6 – (+15,2).

4^О. За три часа работы бригада по уборке снега очистила 43 750 м² дорожного покрытия. За первый час было убрано 32% этой площади, а за второй – 46% оставшейся. Какая площадь была очищена за третий час работы?

5^О. Предприниматель закупил ткань трех видов: шелк, шерсть и ситец. За шелк было уплачено 5760 р., что составило 45% общей стоимости товара. Из суммы, уплаченной за ситец и шерсть, 20% составила стоимость ситца. Определите стоимость шерсти.

Вариант 4

1. Найдите значение выражения:

а) –6,4 + 2,4;	в) –7,4 + 15,7;
б) –1,32 – 0,78;	г) 3,25 – 4,17.

2. Вычислите:

а) ; б) ; в) .

3. Найдите значение алгебраической суммы

–9,7 – (–15,3) + (–0,3) + 14,7.

4^О. На приобретение учебников по истории, биологии и географии школа затратила 32 400 р. За учебники по истории заплатили 28% этой суммы, а за учебники по биологии – 40% остатка. Определите стоимость учебников по географии.

5^О. Котлован для бассейна был отрыт за три недели. За первую неделю вывезли 448 м³ грунта, что составило 28% объема котлована. За вторую неделю вывезли 42% остального вынутого грунта. Каков объем грунта, вывезенного за третью неделю?

Контрольная работа №3

Вариант 1

1. Вычислите:

а) –0,4  7,1; б) ; в) .

2. Отметьте на координатной плоскости точки A(–7;–2), B(2;4), C(1;–5), D(–3;–1).

Запишите координаты точки пересечения отрезка AB и прямой CD.

3 ^О. Найдите значение выражения

(2,4 + 0,78)  (–0,5) – (8,57 – 19,826) : 2,01.

4^О. Дана аналитическая модель числового промежутка: –4 х 3.

Постройте его геометрическую модель и составьте соответствующую символическую запись.

Вариант 2

1. Вычислите:

а) 2,4  (–0,8); б) ; в) .

2. Отметьте на координатной плоскости точки:

A(–5;1), B(5;5), C(–2;8), D(4;–7).

Запишите координаты точки пересечения отрезка AB и прямой CD.

3 ^О. Найдите значение выражения

(4,3 – 6,58)  2,5 + (–16,8 + 70,98) : (–8,4).

4^О. Дана аналитическая модель числового промежутка: х –4.

Постройте его геометрическую модель и составьте соответствующую символическую запись.

Вариант 3

1. Вычислите:

а) 0,7  (–2,8); б) ; в) .

2. Отметьте на координатной плоскости точки A(0;–10), B(4;–2), C(–7;6), D(3;1).

Запишите координаты точки пересечения прямой AB и луча CD.

3 ^О. Найдите значение выражения

–6,4  2,05 + 0,72  5,5 –23,712 : (17,5 – 28,9).

4^О. Дана аналитическая модель числового промежутка: –3 х 4.

Постройте его геометрическую модель и составьте соответствующую символическую запись.

Вариант 4

1. Вычислите:

а) 1,2  (–0,75); б) ; в) .

2. Отметьте на координатной плоскости точки A(–9;0), B(5;–6), C(8;5), D(2;–1).

Запишите координаты точки пересечения отрезка AB и луча CD.

3 ^О. Найдите значение выражения

8,5  (4,1 – 9,58) – 7,32 : (–2,4) + (–4,2) : 2,8.

4^О. Дана аналитическая модель числового промежутка: х 5.

Постройте его геометрическую модель и составьте соответствующую символическую запись.

Контрольная работа №4

Вариант 1

1. Упростите выражение 6(3a – b) – 2(a – 3b).

2. Решите уравнение 10 – 2(3x + 5) = 4(x – 2).

3. В городе два овощных склада. По ошибке на один из них завезли в 4 раза больше картофеля, чем на другой. Чтобы уравнять количество картофеля на обоих складах, пришлось с первого склада перевезти на второй 630 т картофеля. Сколько тонн картофеля было завезено на каждый склад первоначально?

4^О. Вычислите:

.

5^О. Цена яблок – 30 р., а цена груш – 40 р. за 1 кг.

а) На сколько процентов груши дороже яблок?

б) На сколько процентов яблоки дешевле груш?

Вариант 2

1. Упростите выражение 5(4x – y) – 3(y + 2x).

2. Решите уравнение 7(x – 5) + 1 = 2 – 3(2x –1).

3. В результате ошибки, при комплектовании составов пассажирских поездов один состав оказался в полтора раза длиннее другого. Чтобы уравнять число вагонов в обоих поездах, от первого состава отцепили 4 вагона и прицепили их ко второму составу. Сколько вагонов было в каждом составе первоначально?

4 ^О. Вычислите:

.

5^О. Зимние ботинки стоят 2000 р., а осенние 1500 р.

а) На сколько процентов зимние ботинки дороже осенних?

б) На сколько процентов осенние ботинки дешевле зимних?

Вариант 3

1. Упростите выражение –2(8a + 7b) + 4(a – 2b).

2. Решите уравнение 5(2x – 3) – 2(3 – 2x) = 15 – 6(x + 1).

3. Расстояние между двумя городами автомобиль преодолевает за 3 ч. Если бы его скорость была на 15 км/ч больше, то на этот путь эму потребовалось бы 2,4 ч. Определите скорость автомобиля и расстояние между городами.

4 ^О. Вычислите:

.

5^О. Цена карамели – 75 р., а цена шоколадных конфет – 225 р. за 1 кг.

а) На сколько процентов шоколадные конфеты дороже карамели?

б) На сколько процентов карамель дешевле шоколадных конфет?

Вариант 4

1. Упростите выражение 9(2x – 3y) – 8(y – x).

2. Решите уравнение 7(4 – 3x) – (8,5 – x) = 4 – 3(x –8).

3. Расстояние между двумя городами автомобиль преодолевает за 3 ч, а автобус, скорость которого на 18 км/ч меньше – за 3,75 ч. Определите скорость автомобиля и расстояние между городами.

4^О. Вычислите:

.

5^О. Стоимость железнодорожного билета 1800 р., а билета на самолет (по тому же маршруту) – 2700 р.

а) На сколько процентов билет на самолет дороже железнодорожного билета?

б) На сколько процентов железнодорожный билет дешевле билета на самолет?

Контрольная работа №5

Вариант 1

1. Считая, что  = 3,14, определите длину окружности и площадь круга, если радиус R = 5 см.

2. Кукурузой занято 84 га, что составляет площади всего поля. Определите площадь поля.

3. Площадь поля 84 га, из них занято картофелем. Определите площадь, занятую картофелем.

4^О. В первый день Маша прочитала 36% книги, а во второй остатка, после чего ей осталось прочитать 48 страниц. Сколько страниц в книге?

5^О. Вычислите: 8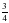 2 – 10 3.

Вариант 2

1. Считая, что  = 3,14, определите длину окружности и площадь круга, если радиус R = 7 см.

2. Площадь поля 75 га, из них занято картофелем. Определите площадь, занятую картофелем.

3. Картофелем занято 75 га, что составляет площади всего поля. Определите площадь поля.

4^О. За первый месяц со склада было вывезено хранившегося там запаса муки, а за второй 15% оставшейся муки, после чего на складе осталось 76.5 т муки. Сколько муки было заложено на хранение на склад?

5^О. Вычислите: –10 : 1 + 3 : 1.

Вариант 3

1. Считая, что  = 3,14, определите длину окружности и площадь круга, если радиус R = 2,5 см.

2. За день турист прошел 24 км, что составило 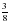длины намеченного маршрута. Определите длину маршрута.

3. Бригада получила задание отремонтировать 24 км дорожного покрытия. За неделю было выполнено 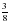этой работы. Сколько километров дороги отремонтировала бригада за неделю?

4^О. При подготовке к математической олимпиаде Миша решал задачи. В первую неделю он решил 55% всех задач, во вторую остатка, а в третью 36 задач. Сколько задач решил Миша при подготовке к олимпиаде?

5^О. Вычислите: 2   – 11 : 3.

Вариант 4

1. Считая, что  = 3,14, определите длину окружности и площадь круга, если радиус R = 4,5 см.

2. Банка, объем которой 630 см³, заполнена водой на своего объема. Найдите объем воды в банке.

3. В банку налито 630 см³ воды, что составляет всего объема банки. Найдите объем банки.

4^О. Бригада по озеленению за первую неделю работы посадила 16% саженцев, за вторую от числа оставшихся саженцев, а за третью – остальные 504 саженца. Сколько саженцев посадила бригада за три недели?

5^О. Вычислите: –3 : 1 + 1 : 1.

Контрольная работа №6

Вариант 1

1. Даны числа 1724, 3965, 7200, 1134.

Выберите те из них, которые делятся:

а) на 2;

б) на 3;

в) на 5.

2. Используя признаки делимости, сократите дробь:

а) ; б) .

3. Можно ли сделать три одинаковых букета из 42 тюльпанов, 21 нарцисса и 6 веточек мимозы?

4^О. Найдите частное: 18ab : (6a).

5^О. На двух складах хранилось 450 т овощей. После того как с одного склада перевезли на другой 75 т овощей, на втором складе овощей стало в 2 раза больше, чем на первом. Сколько тонн овощей было на каждом складе первоначально?

Вариант 2

1. Даны числа 8141, 3615, 4833, 3240.

Выберите те из них, которые делятся:

а) на 3;

б) на 5;

в) на 9.

2. Используя признаки делимости, сократите дробь:

а) ; б) .

3. Имеется 18 карандашей, 36 ручек и 5 блокнотов. Можно ли из них сделать 9 одинаковых наборов?

4^О. Найдите частное: 15xy : (5x)

5^О. В двух кабинетах было 68 стульев. После того как из одного кабинета в другой перенесли 9 стульев, в первом кабинете стульев оказалось в 3 раза меньше, чем во втором. Сколько стульев было в каждом кабинете первоначально?

Вариант 3

1. Даны числа 4875, 2520, 1270, 1719.

Выберите те из них, которые делятся:

а) на 5;

б) на 9;

в) на 10.

2. Используя признаки делимости, сократите дробь:

а) ; б) .

3. Купили 25 белых роз, красных – в 3 раза больше, а желтых – на 15 больше, чем белых. Можно ли из этих цветов составить 5 одинаковых букетов?

4^О. Найдите частное: 21mn : (7m)

5^О. В двух библиотеках было 792 книги. После того, как из одной библиотеки было передано в другую 60 книг, во второй библиотеке книг стало в 2 раза больше, чем в первой. Сколько книг было в каждой библиотеке первоначально?

Вариант 4

1. Даны числа 1710, 1919, 4155, 7428.

Выберите те из них, которые делятся:

а) на 2;

б) на 3;

в) на 10.

2. Используя признаки делимости, сократите дробь:

а) ; б) .

3. Имеется 20 синих карандашей, красных – в 2 раза больше, а простых – на 5 больше, чем синих. Можно ли их них составить 10 одинаковых наборов?

4^О. Найдите частное: 20cd : (4d)

5^О. В двух коробках было 80 пар носков. После того как из одной коробки переложили в другую 14 пар носков, оказалось, что в ней количество носков стало в 3 раза меньше, чем во второй. Сколько пар носков было в каждой коробке первоначально?

Контрольная работа №7

Вариант 1

1. Разложите на простые множители числа: а) 126; б) 84.

2. Найдите: а) НОД (126; 84); б) НОК(126; 84).

3. Сократите дробь .

4^О. Вычислите: .

5^О. Найдите значение выражения

 + 1: .

Вариант 2

1. Разложите на простые множители числа: а) 105; б) 924.

2. Найдите: а) НОД (105; 924); б) НОК(105; 924).

3. Сократите дробь .

4^О. Вычислите: .

5^О. Найдите значение выражения

 + 1 : .

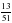Вариант 3

1. Разложите на простые множители числа: а) 630; б) 252.

2. Найдите: а) НОД (630; 252); б) НОК(630; 252).

3. Сократите дробь .

4^О. Вычислите: .

5^О. Найдите значение выражения

 + 1: .

Вариант 4

1. Разложите на простые множители числа: а) 495; б) 825.

2. Найдите: а) НОД (495; 825); б) НОК(495; 825).

3. Сократите дробь .

4^О. Вычислите: .

5^О. Найдите значение выражения

 + 1 : .

Контрольная работа №8

Вариант 1

1. Для изготовления сплава взяли золото и серебро в отношении 2 : 3. Определите, сколько килограммов каждого металла в слитке этого сплава массой 7,5 кг.

2. Перед посадкой семена моркови смешивают с песком в отношении 2 : 5. Определите массу семян, если песка потребовалось 200 г.

3. Для изготовления 12 деталей требуется 0,48 кг металла. Сколько деталей можно изготовить из 0,8 кг металла?

4^О. Вычислите:  + .

5^О. Двигаясь со скоростью 64 км/ч, автобус прибыл в пункт назначения через 3,5 ч. На сколько меньше времени ему потребовалось бы на этот путь, если бы он двигался со скоростью 89,6 км/ч?

Вариант 2

1. Для изготовления 42 кг земляной смеси использовали песок и чернозем в отношении 2 : 5. Определите массу песка и массу чернозема в этой смеси.

2. Для приготовления опары смешали молоко и муку в отношении 3 : 2. Сколько взяли молока (в килограммах), если муки было взято 5 кг?

3. Расход бензина на 760 км составил 49,4 л. Сколько бензина потребуется на 1140 км?

4^О. Вычислите:  + .

5^О. 18 самосвалов одинаковой грузоподъемности могут вывезти грунт за 200 поездок. Сколько самосвалов надо добавить, чтобы сократить число поездок до 150?

Вариант 3

1. Для изготовления смеси взяли чай двух сортов в отношении 3 : 1. Найдите массу чая каждого сорта в 54 кг смеси.

2. Для опрыскивания растений в воде растворяют медный купорос в отношении 1 : 500. Сколько литров воды потребуется, чтобы развести 20 г медного купороса (масса 1 л воды – 1 кг)?

3. Для окрашивания 72 м² поверхности требуется 10,8 л краски. Сколько краски потребуется для окрашивания 126 м² поверхности?

4^О. Вычислите:  + .

5^О. Для расфасовки крупы понадобилось 50 пакетов вместимостью 0,9 кг. На сколько больше пакетов вместимостью 0,5 кг потребуется для расфасовки того же количества муки?

Вариант 4

1. Для изготовления начинки для пирога смешали курагу с черносливом в отношении 4 : 1. Определите массу каждого компонента в 37 кг начинки.

2. Для приготовления молочного коктейля смешивают молоко с мороженым в отношении 5 : 2. Сколько потребуется мороженого на 3 л молока (считаем, что масса 1 л молока – 1 кг)?

3. Для изготовления 15 платьев требуется 48 м ткани. Сколько ткани потребуется на изготовление 22 таких же платьев?

4^О. Вычислите:  + .

5^О. Двигаясь со скоростью 75 км/ч, поезд прибыл в пункт назначения через 4,2 ч. На сколько поезд должен увеличить скорость, чтобы сократить время в пути до 3 ч?

Итоговая контрольная работа за курс 6 класса

Вариант 1

1. Вычислите: .

2. Выполните действия: .

3. Упростите выражение 5(3 + 2x) – 2(12 – 8x).

4. В одной цистерне в 4 раза меньше нефти, чем во второй. После того как в первую цистерну добавили 20 т нефти, а из второй откачали 19 т, нефти в обеих цистернах стало поровну. Сколько тонн нефти было в каждой цистерне первоначально?

5. Туристы были в пути 3 дня. В первый день они преодолели 36% всего расстояния, во второй 52% оставшегося, а в третий – 54 км. Найдите длину всего пути.

Вариант 2

1. Вычислите: .

2. Выполните действия: .

3. Упростите выражение –7(6x + 3) – 5(4 – x).

4. На одном складе было в 2,5 раза меньше овощей, чем на второй. После того как на первый склад завезли 180 т овощей, а на второй 60 т, овощей на обоих складах стало поровну. Сколько тонн овощей было на каждом складе первоначально?

5. Поле, площадью 18 га вспахали за 3 дня. В первый день вспахали 35% всего поля, а во второй 40% оставшейся площади. Сколько гектаров вспахали в третий день?

Вариант 3

1. Вычислите: .

2. Выполните действия: .

3. Упростите выражение –3(4 –2x) + 7(x – 2).

4. В одном мешке в полтора раза больше муки, чем во втором. После того как из первого мешка достали 35 кг муки, а из второго 17 кг, муки в обоих мешках стало поровну. Сколько килограммов муки было в каждом мешке первоначально?

5. Картофель, закупленный предпринимателем, был продан в три магазина. В первый магазин было продано 25% всего картофеля, во второй – 60% остатка, а в третий остальные 1,5 т. Определите массу картофеля, закупленного предпринимателем.

Вариант 4

1. Вычислите: .

2. Выполните действия: .

3. Упростите выражение 4(3x – 1) – 8(2x + 5).

4. На одной стоянке было в 3 раза меньше автомашин, чем на второй. После того как на первую стоянку приехали 18 автомашин, а со второй уехали 10, автомашин на обеих стоянках стало поровну. Сколько автомашин было на каждой стоянке первоначально?

5. На выполнение домашних заданий по математике, литературе и географии Митя потратил 1 ч 40 мин. На математику у него ушло 40% этого времени, на литературу – 45% остального. Сколько времени Митя выполнял задание по географии?

Литература для обучающихся

1. Зубарева, И.И. Математика. 5 класс. Учебник для учащихся общеобразовательных учреждений [Текст] / И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2012. − 270с.

2. Зубарева, И.И. Математика. 6 класс. Учебник для учащихся общеобразовательных учреждений [Текст] / И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2012. − 264с.

3. Зубарева, И.И. Математика. 5 класс. Рабочая тетрадь №1, №2[Текст]/ И.И. Зубарева. – М.: Мнемозина, 2011.

4. Зубарева, И.И. Математика. 6 класс. Рабочая тетрадь №1, №2[Текст]/ И.И. Зубарева. – М.: Мнемозина, 2011.

5. Зубарева, И.И. Математика. 5 класс. Самостоятельные работы[Текст]/ И.И. Зубарева, И.П. Лешенкова, М.С. Мильштейн.– М: Мнемозина, 2012.

6. Зубарева, И.И. Математика. 6 класс. Самостоятельные работы[Текст] / И.И. Зубарева, И.П. Лешенкова, М.С. Мильштейн.– М: Мнемозина, 2012.

7. Математика 5 класс. [Электронный ресурс]. Серия 1С: школа, платформа 1С: Образование 3.0,2011.

8. Математика 6 класс. [Электронный ресурс]. Серия 1С: школа, платформа 1С: Образование 3.0,2011.

Литература для педагога

1. Зубарева, И.И. Математика. 5 класс. Учебник для учащихся общеобразовательных учреждений [Текст] / И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2012. − 270с.

2. Зубарева, И.И. Математика. 6 класс. Учебник для учащихся общеобразовательных учреждений [Текст] / И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2012. − 264с.

3. Зубарева, И.И. Математика. 5 класс. Самостоятельные работы[Текст]/ И.И. Зубарева, И.П. Лешенкова, М.С. Мильштейн.– М: Мнемозина, 2012.

4. Зубарева, И.И. Математика. 6 класс. Самостоятельные работы[Текст]/ И.И. Зубарева, И.П. Лешенкова, М.С. Мильштейн.– М: Мнемозина, 2012.

5. Зубарева, И.И. Математика. 5-6 классы[Текст]:Методическое пособие для учителя/И.И. Зубарева, А.Г. Мордкович.– М: Мнемозина, 2008.

6. Математика 5 класс. [Электронный ресурс]. Серия 1С: школа, платформа 1С: Образование 3.0,2011.

7. Математика 6 класс. [Электронный ресурс]. Серия 1С: школа, платформа 1С: Образование 3.0,2011.