Данная программа по алгебре и началам математического анализа для 10 класса рассчитана на 105 часов из расчета 3 часа в неделю. Программа составлена на основе программы «Алгебра и начала математического анализа 10-11 классы», авторы И.И. Зубарева, А.Г. Мордкович, М.: Мнемозина 2009, учебника А.Г. Мордковича «Алгебра и начала математического анализа 10 - 11» М: Мнемозина 2014.
Определение функции, способы её задания, свойства функций. Обратная функция.
Знакомство с моделями «числовая окружность» и «числовая окружность на координатной плоскости». Синус, косинус как координаты точки числовой окружности, тангенс и котангенс. Тригонометрические функции числового аргумента и связи между ними. Тригонометрические функции углового аргумента, радианная мера угла. Функции y=sin x, y═cos x, их свойства и графики. Формулы приведения. Периодичность функций y=sin x, y═cos x.
Решение тригонометрических уравнений методом введения новой переменной и разложения на множители; однородные тригонометрические уравнения.
Синус и косинус суммы и разности аргументов. Тангенс суммы разности аргументов. Формулы двойного аргумента, формулы понижения степени. Формулы половинного угла. Преобразования сумм тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование выражения А sin x + В cos x к виду С sin (x + t).
Преобразования простейших тригонометрических выражений.
Числовые последовательности (определение, параметры, свойства). Понятие предела последовательности (на наглядно-интуитивном уровне). Существование предела монотонной ограниченной последовательности (простейшие случаи вычисления пределов последовательности: длина окружности и площадь круга как пределы последовательностей; вычисление суммы бесконечной геометрической прогрессии). Предел функции на бесконечности и в точке.
Приращение аргумента, приращение функции. Определение производной: задачи, приводящие к понятию производной, определение производной, ее геометрический и физический смысл, алгоритм отыскания производной.
Вычисление производных: формулы дифференцирования для функций у = С, у = kx+m,
y = x, y = 1/x, y =√x, y = sin x, y = cos x), правила дифференцирования (суммы, произведения, частного), дифференцирование функций y = x ³, y = tg x, y = ctg x, y = xª , дифференцирование функции y = f (kx + m).
Уравнение касательной к графику функции.
Применение производной для исследования функций: исследование функций на монотонность, отыскание точек экстремума, построение графиков функций. Отыскание наибольших и наименьших значений непрерывной функции на промежутке, задачи на отыскание наибольших и наименьших значений величин.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком.
• значение математической науки для решения задач, возникающих в теории и практике; широту и в тоже время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
• значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
• возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
• вероятностный характер различных процессов окружающего мира.
| № урока | Дата | Тема урока | Кол-во часов | Элементы содержания | Требования к уровню подготовки | Контроль за усвоением знаний |
|
| Глава1. Числовые функции (5ч) |
|
| 1 чет 1 | 02.09 |
Числовая функция. |
2 | Понятие функции. Область определения и область значений функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, ограниченность функции, непрерывность. Четные и нечетные функции. Обратная функция.
| Уметь находить значения функции, заданной формулой, таблицей, графиком по ее аргументу. Уметь находить значение аргумента по значению функции, заданной графиком или таблицей. Уметь определять свойства функции по ее графику.
|
|
| 2 | 03.09 |
Числовая функция. |
|
| 3 | 05.09 | Свойства функции.
| 2 |
|
| 4 | 09.09 | Свойства функции.
|
|
| 5 | 10.09 | Обратная функция. | 1 |
|
|
| Глава2. Тригонометрические функции(32ч) |
|
| 6 | 12.09 | Входная контрольная работа по расписанию. | 1 |
|
| К.р. |
| 7 | 16.09 | Числовая окружность. | 2 | Радианная мера угла. Поворот точки вокруг начала координат. Основные тригонометрические формулы. Тригонометрические тождества. Тригонометрические функции.
| Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц. Выполнять тождественные преобразования тригонометрических выражений с помощью справочного материала.
|
|
| 8 | 17.09 | Числовая окружность. |
|
| 9 | 19.09 | Числовая окружность на координатной плоскости. | 2 |
|
| 10 | 24.09 | Числовая окружность на координатной плоскости. |
|
| 11 | 03.10 | Синус и косинус. Тангенс и котангенс. | 5 |
|
| 12 | 04.10 | Синус и косинус. Тангенс и котангенс. |
|
| 13 | 07.10 | Синус и косинус. Тангенс и котангенс. | Т.д. |
| 14 | 08.10 | Синус и косинус. Тангенс и котангенс. |
|
| 15 | 09.10 | Синус и косинус. Тангенс и котангенс. |
|
| 16 | 09.10 | Контрольная работа №1 «Числовые функции» | 1 | К.р. |
| 17 | 10.10 | Тригонометрические функции числового аргумента. | 3 | Радианная мера угла. Поворот точки вокруг начала координат. Основные тригонометрические формулы. Тригонометрические тождества. Тригонометрические функции. Формулы приведения.
| Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц. Уметь применять формулы приведения для вычисления значения тригонометрических функций тупых углов, для упрощения выражений. |
|
| 18 | 14.10 | Тригонометрические функции числового аргумента. |
|
| 19 | 15.10 | Тригонометрические функции числового аргумента. |
|
| 20 | 17.10 | Тригонометрические функции углового аргумента. | 2 |
|
| 21 | 18.10 | Тригонометрические функции углового аргумента. |
|
| 22 | 21.10 | Формулы приведения. | 3 |
|
| 23 | 22.10 | Формулы приведения. | С.р. |
| 24 | 24.10 | Формулы приведения. |
|
| 25 | 28.10 | Контрольная работа №2 «Тригонометрические функции» | 1 |
|
| К.р. |
| 26 | 29.10 | Функция y=sin x, ее свойства и график. | 2 | Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса углов. Определение тригонометрических функций, их свойства, графики.
| Знать свойства тригонометрических функций 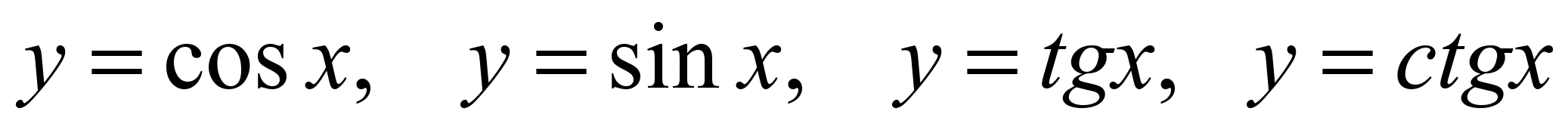 и уметь строить их графики. и уметь строить их графики.
|
|
| 27 | 31.10 | Функция y=sin x, ее свойства и график. |
|
| 2 чет 28 | 11.11 | Функция y=cos x, ее свойства и график. | 2 |
|
| 29 | 12.11 | Функция y=cos x, ее свойства и график. |
|
| 30 | 14.11 | Периодичность функций y=sin x, y=cos x. | 2 |
|
| 31 | 18.11 | Периодичность функций y=sin x, y=cos x. |
|
| 32 | 19.11 | Преобразование графиков тригонометрических функций. | 3 |
|
| 33 | 21.11 | Преобразование графиков тригонометрических функций. |
|
| 34 | 25.11 | Преобразование графиков тригонометрических функций. |
|
| 35 | 26.11 | Функции y=tg x, y=ctg x, их свойства и графики. | 2 | Пр.р. |
| 36 | 28.11 | Функции y=tg x, y=ctg x, их свойства и графики. |
|
| 37 | 02.12 | Контрольная работа №3 «Функции y=sin x, y=cos x, y=tg x, y=ctg x». | 1 |
|
| К.р. |
|
| Глава3. Тригонометрические уравнения (14ч) |
|
| 38 | 03.12 | Арккосинус. Решение уравнения cos t=a. | 3 | Арккосинус, арксинус, арктангенс, арккотангенс. Основные правила решения простейших тригонометрических уравнений. | Знать определение арккосинуса, арксинуса, арктангенса, арккотангенса, правила решения простейших тригонометрических уравнений. Уметь решать тригонометрические уравнения. |
|
| 39 | 05.12 | Арккосинус. Решение уравнения cos t=a. |
|
| 40 | 09.12 | Арккосинус. Решение уравнения cos t=a. |
|
| 41 | 10.12 | Арксинус. Решение уравнения sin t=a. | 3 |
|
| 42 | 12.12 | Арксинус. Решение уравнения sin t=a. |
|
| 43 | 16.12 | Арксинус. Решение уравнения sin t=a. |
|
| 44 | 17.12 | Арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a. | 1 | С.р. |
| 45 | 19.12 | Административная контрольная работа за 1 полугодие по расписанию. | 1 | К.р. |
| 46 | 23.12 | Арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a. | 1 |
|
| 47 | 24.12 | Решение тригонометрических уравнений. | 4 |
|
| 48 | 26.12 | Решение тригонометрических уравнений. | Основные правила решения простейших тригонометрических уравнений. | Уметь решать тригонометрические уравнения. |
|
| 3 чет
49 |
| Решение тригонометрических уравнений. |
|
| 50 |
| Решение тригонометрических уравнений. |
|
| 51 |
| Контрольная работа №4 «Решение тригонометрических уравнений». | 1 |
|
| К.р. |
|
| Глава4. Преобразование тригонометрических выражений (14ч) |
|
| 52 |
| Синус и косинус суммы и разности аргументов. | 3 | Основные тригонометрические тождества: синус и косинус суммы и разности аргументов, тангенс суммы и разности аргументов, формулы двойного аргумента, преобразование сумм тригонометрических функций в произведения. | Знать основные тригонометрические тождества. уметь применять тригонометрические тождества при преобразовании выражений. |
|
| 53 |
| Синус и косинус суммы и разности аргументов. |
|
| 54 |
| Синус и косинус суммы и разности аргументов. |
|
| 55 |
| Тангенс суммы и разности аргументов. | 2 |
|
| 56 |
| Тангенс суммы и разности аргументов. |
|
| 57 |
| Формулы двойного аргумента. | 3 |
|
| 58 |
| Формулы двойного аргумента. |
|
| 59 |
| Формулы двойного аргумента. |
|
| 60 |
| Преобразование сумм тригонометрических функций в произведения. | 2 |
|
| 61 |
| Преобразование сумм тригонометрических функций в произведения. |
|
| 62 |
| Преобразование произведений тригонометрических функций в суммы. | 2 | Т.д. |
| 63 |
| Преобразование произведений тригонометрических функций в суммы. |
|
| 64 |
| Преобразование тригонометрических выражений. | 1 |
|
| 65 |
| Контрольная работа №5 «Преобразование тригонометрических выражений» | 1 |
|
| К.р. |
|
| Глава5. Производная(27ч) |
|
| 66 |
| Предел последовательности. | 1 | Понятие о пределе и непрерывности функции. Понятие производной. Производная степенной функции. Производная суммы, произведения и частного двух функций. Производные тригонометрических функций.
| Знать определение предела функции, производной, правила вычисления производных. Уметь вычислять производные. |
|
| 67 |
| Сумма бесконечной геометрической прогрессии. | 2 |
|
| 68 |
| Сумма бесконечной геометрической прогрессии. |
|
| 69 |
| Предел функции. | 2 |
|
| 70 |
| Предел функции. |
|
| 71 |
| Определение производной. | 2 |
|
| 72 |
| Определение производной. |
|
| 73 |
| Вычисление производных. | 3 | Пр.р. |
| 74 |
| Вычисление производных. |
|
| 75 |
| Вычисление производных. |
|
| 76 |
| Контрольная работа №6 «Производная». | 1 |
|
| К.р. |
| 77 |
| Уравнение касательной. | 2 | Уравнение касательной, применение производной при исследовании функций. Возрастание, убывание функции, экстремумы. | Знать уравнение касательной, признаки возрастания и убывания функции, точек экстремума. Уметь составлять уравнение касательной, исследовать функцию на монотонность, экстремумы. |
|
| 78 |
| Уравнение касательной. |
|
| 4 чет 79 |
| Применение производной для исследования функций на монотонность и экстремумы. | 4 |
|
| 80 |
| Применение производной для исследования функций на монотонность и экстремумы. |
|
| 81 |
| Применение производной для исследования функций на монотонность и экстремумы. |
|
| 82 |
| Применение производной для исследования функций на монотонность и экстремумы. |
|
| 83 |
| Построение графиков функций. | 3 | С.р. |
| 84 |
| Построение графиков функций. | Построение графиков функций. | Уметь строить графики функций. |
|
| 85 |
| Построение графиков функций. |
|
| 86 |
| Контрольная работа №7 «Применение производной для исследования функций». | 1 |
|
| К.р. |
| 87 |
| Применение производной для нахождения наибольших и наименьших значений величин. | 3 | Применение производной при нахождении наибольшего и наименьшего значения. | Уметь использовать производную при исследовании функции, при отыскании наибольшего и наименьшего значения. |
|
| 88 |
| Применение производной для нахождения наибольших и наименьших значений величин. |
|
|
| 89 |
| Применение производной для нахождения наибольших и наименьших значений величин. |
|
|
| 90 |
| Задачи на отыскание наибольших и наименьших значений величин. | 2 |
|
| 91 |
| Задачи на отыскание наибольших и наименьших значений величин. |
|
|
|
| 92 |
| Контрольная работа № 8 «Применение производной для нахождения наибольших и наименьших значений величин». | 1 |
|
| К.р. |
|
| Итоговое повторение(13ч) |
|
| 93 |
| Повторение. Решение тригонометрических уравнений. | 4 |
|
|
|
| 94 |
| Повторение. Решение тригонометрических уравнений. |
|
|
|
| 95 |
| Повторение. Решение тригонометрических уравнений. |
|
|
|
| 96 |
| Повторение. Решение тригонометрических уравнений. |
|
|
|
| 97 |
| Повторение. Преобразование тригонометрических выражений. | 4 |
|
|
|
| 98 |
| Повторение. Преобразование тригонометрических выражений. |
|
|
|
| 99 |
| Повторение. Преобразование тригонометрических выражений. |
|
|
|
| 100 |
| Повторение. Преобразование тригонометрических выражений. |
|
|
|
| 101-102 |
| Итоговая контрольная работа по расписанию. | 2 |
|
| К.р. |
| 103 |
| Повторение. Производная. | 3 |
|
|
|
| 104 |
| Повторение. Производная. |
|
|
|
| 105 |
| Повторение. Производная. |
|
|
|
|
|
| Итого: 105 часов. |
|
|
|
|
















