Пояснительная записка
Данная учебная рабочая программа ориентирована на учащихся 9 класса и реализуется на основе следующих нормативных правовых документов:
Федеральный закон «Об образовании в Российской Федерации» от 29 декабря 2012 г № 273-ФЗ;
Приказ МО и науки РФ от 05.03.2004г №1089 «Об утверждении Федерального компонента государственных стандартов начального, общего, основного общего и среднего (полного) общего образования»;
Примерные программы, созданные на основе федерального компонента государственного образовательного стандарта;
Программы. Математика. 5 – 6 классы. Алгебра. 7 – 9 классы. Алгебра и начала анализа. 10 – 11 классы / авт.-сост. И. И. Зубарева, А. Г. Мордкович.
Приказ МО и науки РФ от 31.03.2014г №253 «Об утверждении федерального перечня учебников, рекомендуемых к использованию при имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;
Приказ Министерства образования Оренбургской области от 13.08.2014 г. № 01-21/1063 «Об утверждении регионального базисного учебного плана и примерных учебных планов для общеобразовательных организаций Оренбургской области»;
Образовательная программа образовательной организации МБОУ «Буртинская СОШ»
Учебный план МБОУ «Буртинская СОШ» на 2014-2015 учебный год;
Календарный учебный график.
Образовательная деятельность осуществляется на основании лицензии серии РО №049433 от 06.03.2012г. на бессрочный срок деятельности.
Цели обучения с учетом специфики учебного предмета.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
в направлении личностного развития
формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие интереса к математическому творчеству и математических способностей;
в метапредметном направлении
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
в предметном направлении
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Задачи обучения по предмету.
Образовательные и воспитательные задачи обучения алгебре должны решаться комплексно с учетом возрастных особенностей обучающихся, специфики алгебры как учебного предмета, определяющего её роль и место в общей системе школьного обучения и воспитания.
Задачами обучения математики являются:
Приобретение математических знаний и умений;
освоение компетенций (учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, информационно-технологической, ценностно-смысловой).
формирование элементов самостоятельной интеллектуальной деятельности на основе овладения математическими методами познания окружающего мира (умения устанавливать, описывать, моделировать и объяснять количественные и пространственные отношения);
развитие основы логического, знаково-символического и алгоритмического мышления; пространственного воображения; математической речи; умения вести поиск информации и работать с ней;
развитие познавательных способностей;
воспитывать стремление к расширению математических знаний;
способствовать интеллектуальному развитию, формированию качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, интуиции, логического мышления, пространственных представлений, способности к преодолению трудностей;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
готовность к сотрудничеству с другими людьми, доверие к другим людям, коллективизм;
ответственность за принятые решения, действия и поступки перед самим собой и другими людьми;
обеспечить уровневую дифференциацию в ходе обучения;
сформировать устойчивый интерес учащихся к предмету
духовно-нравственное развитие личности, предусматривающее, с учётом специфики начального этапа обучения математике, принятие нравственных установок созидания, справедливости, добра, становление основ гражданской российской идентичности, любви и уважения к своему Отечеству;
формирование математического языка и математического аппарата как средства описания и исследования окружающего мира и как основы компьютерной грамотности;
реализация возможностей математики в формировании научного мировоззрения учащихся, в освоении ими научной картины мира с учётом возрастных особенностей учащихся;
овладение системой математических знаний, умений и навыков, необходимых для повседневной жизни и для продолжения образования в средней школе;
расширение класса функций, свойства и графики которых известны учащимся; дальнейшее формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, её области определения, ограниченности, непрерывности, наибольшего и наименьшего значений на заданном промежутке;
развитие представление о числе и роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контр примеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства
В основу курса алгебры для 9 класса положены такие принципы как:
Целостность и непрерывность, означающие, что данная ступень является важным звеном единой общешкольной подготовки по математике.
Научность в сочетании с доступностью, строгость и систематичность изложения (включение в содержание фундаментальных положений современной науки с учетом возрастных особенностей обучаемых
Практико-ориентированность, обеспечивающая отбор содержания, направленного решение простейших практических задач планирования деятельности, поиска нужной информации.
Принцип развивающего обучения (обучение ориентировано не только на получение новых знаний, но и активизацию мыслительных процессов, формирование и развитие у школьников обобщенных способов деятельности, формирование навыков самостоятельной работы).
Место предмета
Предмет алгебра относится к образовательной области «Математика», изучается в течение 7 – 9 классов, впервые начинает изучаться в 7 классе. На изучение предмета в 9 классе отводится 4 часа в неделю: всего 136 часа за учебный год. (1 час добавлен из школьного компонента Учебного плана). Предусмотрено 6 тематических контрольных работ , 1 итоговая контрольная работа за 1 полугодие и 1 итоговая контрольная работа по учебному материалу алгебры 9 класса.
Данная рабочая программа полностью отражает базовый уровень подготовки обучающихся по разделам программам. Программа рассчитана на 1 год обучения.
Программа построена с учетом принципов системности, научности и доступности, а также преемственности и перспективности между различными разделами курса
Общая характеристика курса алгебры в 9 классе.
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы.
Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно – научного цикла, в частности к физике. Развитие логического мышления учащихся при обучении математике способствует усвоению предметов гуманитарного цикла. Практические умения и навыки математического характера необходимы для трудовой и профессиональной подготовки школьников.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира.
Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладения навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству.
Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, периодических и др.) для формирования у школьников представления о роли математики в развитии цивилизации и культуры.
При изучении алгебры обогащаются представления о современной картине мира и методов его исследования, развиваются представления о числе и роли вычислений в человеческой практике, используются функционально-графические представления для описания и анализа реальных зависимостей.
Особенностью курса является то, что он базируется на функционально - графическом подходе. Это выражается в том, что какой бы класс функций, уравнений и выражений не изучался, построение материала практически всегда осуществляется по жёсткой схеме: Функция – Уравнения – Преобразования.
Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.
Содержание учебного предмета
ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ 8 КЛАССА (5 Ч.)
Входная диагностика
Глава I. НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ (19 Ч.)
Линейное и квадратное неравенство с одной переменной, частное и общее решение, равносильность, равносильные преобразования. Рациональные неравенства с одной переменной, метод интервалов, кривая знаков, нестрогие и строгие неравенства. Элемент множества, подмножество данного множества, пустое множество. Пересечение и объединение множеств. Системы линейных неравенств, частное и общее решение системы неравенств.
Контрольная работа № 1 по теме «Неравенства с одной переменной. Системы и совокупности неравенств»
Основная цель:
· формирование представлений о частном и общем решении рациональных неравенств и их систем, о неравенствах с модулями, о равносильности неравенств;
· овладение умением совершать равносильные преобразования, решать неравенства методом интервалов;
· расширение и обобщение сведений о рациональных неравенствах и способах их решения: метод интервалов, метод замены переменной.
Глава II. системы уравнений (21 ч.)
Рациональное уравнение с двумя переменными, решение уравнения с двумя переменными р(х;у) = 0, равносильные уравнения с двумя переменными, равносильные преобразования. Формула расстояния между двумя точками координатной плоскости. График уравнения (х - а)2 + {у - b)2 = r2. Система уравнений с двумя переменными, решение системы уравнений с двумя переменными. Метод подстановки, метод алгебраического сложения, метод введения новых переменных, графический метод. Равносильность систем уравнений. Системы уравнений как математические модели реальных ситуаций.
Контрольная работа № 2 по теме «Системы уравнений»
Основная цель:
· формирование представлений о системе двух рациональных уравнений с двумя переменными, о рациональном уравнении с двумя
переменными;
· овладение умением совершать равносильные преобразования, решать уравнения и системы уравнений с двумя переменными;
· отработка навыков решения уравнения и системы уравнений различными методами: графическим, подстановкой, алгебраического
сложения, введения новых переменных.
Глава III. Числовые функции (29 ч.)
Функция, область определение и множество значений функции. Аналитический, графический, табличный, словесный способы задания функции. График функции. Монотонность (возрастание и убывание) функции, ограниченность функции снизу и сверху, наименьшее и наибольшее значения функции, непрерывная функция, выпуклая вверх или вниз. Исследование элементарных функций: у = С, у = kx + т,
у = kx2, у=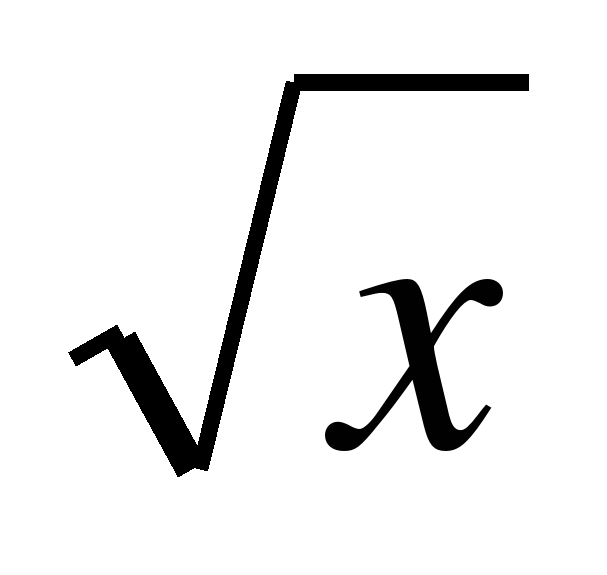
, 
=
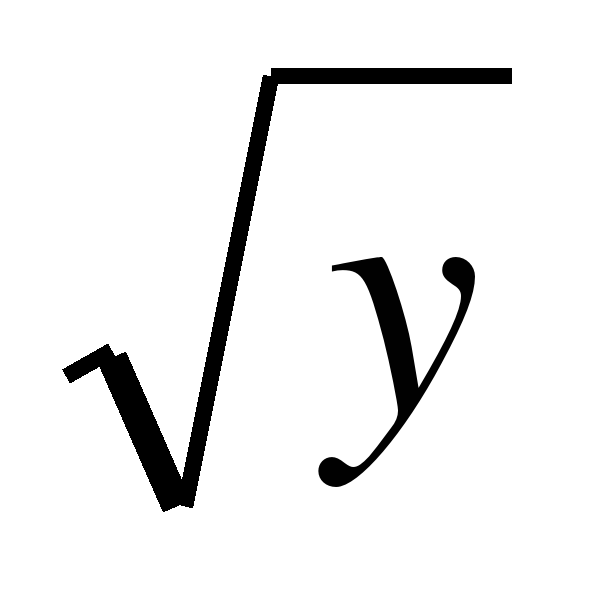, у =
, у =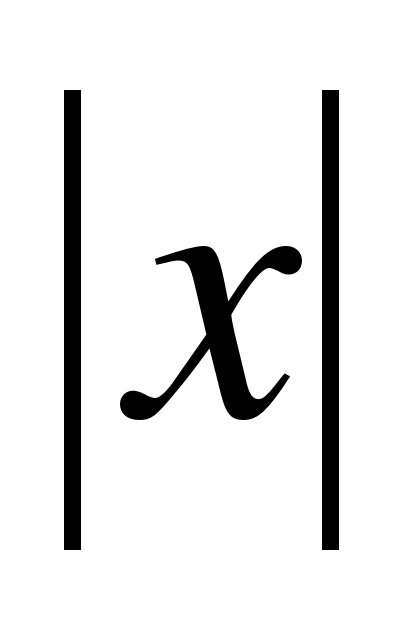 ах2 + bх + с. Четная и нечетная функции. Алгоритм исследования функции на четность. Графики четной и нечетной функций. Степенные функции с натуральным показателем, их свойства и графики. Свойства и графики степенных функций с четным и нечетным показателями, с отрицательным целым показателем.
Контрольная работа № 3 по теме «Числовые функции и их свойства».
Контрольная работа № 4 по теме «Числовые функции и их свойства»
Основная цель:
· формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, её области
определения, области значения; о различных способах задания функции: аналитическом, графическом, табличном, словесном;
· овладение умением применения четности или нечетности, ограниченности, непрерывности, монотонности функций;
· формирование умений находить наибольшее и наименьшее значение на заданном промежутке, решая практические задачи;
· формирование понимания того, как свойства функций отражаются на поведении графиков функций
Глава IV. Прогрессии (22 ч.)
Числовая последовательность. Способы задания числовой последовательности(аналитический, словесный, рекуррентный). Свойства числовых последовательностей, монотонная последовательность, возрастающая последовательность, убывающая последовательность. Арифметическая прогрессия, её разность, возрастающая прогрессия, конечная прогрессия, формула n-го члена арифметической прогрессии, формула суммы членов конечной арифметической прогрессии, характеристическое свойство арифметической прогрессии. Геометрическая прогрессия, знаменатель прогрессии, возрастающая прогрессия, конечная прогрессия, формула n-го члена геометрической прогрессии, формула суммы членов конечной геометрической прогрессии, характеристическое свойство геометрической прогрессии. Прогрессии и банковские расчеты.
Контрольная работа № 5 по теме «Арифметическая прогрессия».
Основная цель:
· формирование преставлений о понятии числовой последовательности, арифметической и геометрической прогрессиях как частных случаях числовых последовательностей; о трех способах задания последовательности: аналитическом, словесном и рекуррентном;
· сформировать и обосновать ряд свойств арифметической и геометрической прогрессий, свести их в одну таблицу;
· овладение умением решать текстовые задачи, используя свойства арифметической и геометрической прогрессии.
Глава V. элементы комбинаторики, статистики и теории вероятностей (20 ч)
Методы решения простейших комбинаторных задач (перебор вариантов, построение дерева вариантов, правило умножения). Факториал. Перестановки. Размещения. Сочетания. Общий ряд данных и ряд данных конкретного измерения, варианта ряда данных, её кратность, частота и процентная частота, сгруппированный ряд данных, многоугольники распределения. Объем, среднее арифметическое, размах, мода, медиана, среднее значение. Вероятность. Событие (случайное, достоверное, невозможное). Несовместные события. Противоположные события. Вероятность суммы двух событий. Вероятность противоположного события. Классическая вероятностная схема. Классическое определение вероятности. Статистическая устойчивость. Статистическая вероятность.
Контрольная работа № 6 по теме «Элементы комбинаторики, статистики и теории вероятностей».
Основная цель:
· формирование преставлений о всевозможных комбинациях, о методах статистической обработки результатов измерений, полученных при проведении эксперимента, о числовых характеристиках информации;
· овладеть умением решения простейших комбинаторных и вероятностных задач.
ГЛАВА VI. ИТОГОВОЕ ПОВТОРЕНИЕ И ПОДГОТОВКА К ЭКЗАМЕНУ (17 Ч)
Итоговая контрольная работа № 7.
Основная цель – подготовить учащихся к итоговой аттестации.
Список умений, на овладение которых может быть направлена работа по повторению:
– выполнение преобразований целых и дробных выражений, действия над степенями с целыми показателями;
– выполнение преобразований числовых выражений, содержащих квадратные корни;
– нахождение значений буквенных выражений при заданных значениях букв;
– решение линейных и квадратных уравнений, простейших дробно-рациональных уравнений;
– решение систем двух уравнений первой степени и систем, в которых одно из уравнений – второй степени;
– решение задач методом уравнений;
– решение линейных неравенств и их систем, неравенств второй степени, применение свойств неравенств для оценки значений выражений;
– построение и чтение графиков линейной и квадратичной функций, прямой и обратной пропорциональностей;
– вычисление координат точек пересечения прямых, прямой и параболы, нахождение нулей функций, вычисление координат точек пересечения графиков с осями координат;
– интерпретация графиков реальных зависимостей.
Повторение построено следующим образом: на первом уроке повторяются, обобщаются и систематизируются полученные знания по данной теме, затем на втором уроке в классе проводится тест по этой теме, где задания расположены по возрастанию уровня сложности, задания с выбором ответа или с кратким ответом. На следующем уроке производится работа над ошибками: полный разбор заданий, где допущены ошибки и рефлексия. Такое повторение материала дает возможность учащимся понять, на что нужно обратить внимание, это поможет учащимся сориентироваться в экзаменационных требованиях, понять критерии оценивания работы.
Тематическое планирование
| № | Тема раздела | Кол-во час | Характеристика основных видов деятельности |
| по авторской прогр | по данной РП |
|
|
| Повторение | 4 | 5 | Распознавать линейные и квадратные неравенства; решать рациональные неравенства и системы неравенств; использовать теоретико – множественную символику; использовать в письменной математической речи обозначения и графические изображения числовых множеств. |
| Глава I. Неравенства и системы неравенств | 18 | 19 |
| 1 | Линейные и квадратные неравенства | 3 | 4 |
| 2 | Рациональные неравенства. | 5 | 5 |
| 3 | Множество операций над ними | 4 | 4 |
| 4 | Системы рациональных неравенств. | 5 | 5 |
|
| Контрольная работа № 1 | 1 | 1 |
| Глава II. Системы уравнений | 21 | 21 | Определять является ли пара чисел решением системы уравнений; Строить графики уравнений с двумя переменными; решать системы уравнений второй степени различными способами (графическим, подстановки, алгебраического сложения, введение новых переменных); решать текстовые задачи с помощью систем уравнений второй степени. |
| 5 | Основные понятия.
| 6 | 6 |
| 6 | Методы решения систем уравнений.
| 6 | 6 |
| 7 | Система уравнений как математические модели реальных ситуаций. | 8 | 8 |
|
| Контрольная работа № 2
| 1 | 1 |
| Глава III. Числовые функции | 29 | 29 | Вычислять значения функция заданных формулами; Составлять таблицы значений функций; Использовать функциональную символику для записи ; Использовать функционально – графическое представление для исследования и решения уравнений; Уметь находить область определения функции и область значения функции, ограниченность функции, наибольшее и наименьшее значение функции, возрастания и убывания функции, четности и нечетности функции, строить и читать графики функций; уметь в построении графиков степенной функции и их прочтении; . |
| 8 | Определение числовой функции. Область определения, область значений функции | 5 | 5 |
| 9 | Способы задания функции. | 3 | 3 |
| 10 | Свойства функции.
| 5 | 5 |
| 11 | Четные и нечетные функции. | 3 | 3 |
|
| Контрольная работа № 3 | 1 | 1 |
| 12 |
Функция у = хn (n  N), их свойства и график. | 4 | 4 |
| 13 | Функция у = х-n (n N), их свойства и график. | 4 | 4 |
| 14 | Функция у = 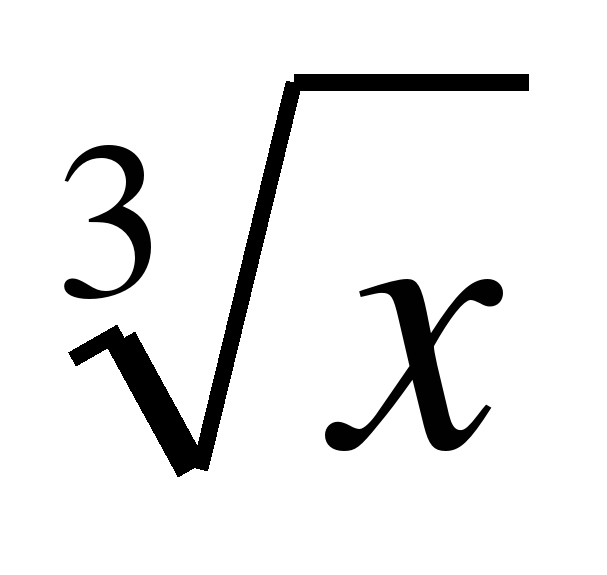 ,её свойства и график. | 3 | 3 |
|
| Контрольная работа № 4 | 1 | 1 |
|
| Глава IV. Прогрессии | 22 | 22 | Применять индексные обозначения, строить речевые высказывания с использованием терминологии, связанной с понятием числовой последовательности; Находить члены числовой последовательности по формуле и применять свойства в ходе выполнения упражнений; решать задачи, используя формулу n – го члена арифметической и геометрической прогрессии, решать задачи с использованием формул суммы n первых членов арифметической и геометрической прогрессии, находить суммы членов конечной геометрической прогрессии. |
| 15 | Числовые последовательности.
|
6
| 6 |
| 16 | Арифметическая прогрессии.
| 7 | 7 |
| 17 | Геометрическая прогрессия. | 8 | 8 |
|
| Контрольная работа № 5
| 1 | 1 |
| Глава V. Элементы логики, комбинаторики, статистики и теории вероятности | 20 | 20 | Выполнять перебор всех возможных вариантов для пересчета объектов и комбинаций; применять правило комбинаторного умножения для решения на нахождение числа объектов или комбинации; решать задачи на определение достоверных, невозможных и случайных событий, перебор вариантов; кратности варианта, частоты варианта ; извлекать информацию из таблиц и диаграмм; выполнять вычисления по табличным данным; организовать информацию в виде таблиц и диаграмм. |
| 18 | Комбинаторные задачи. Самостоятельная работа | 5 | 5 |
| 19 | Статистика – дизайн информации | 5 | 5 |
| 20 | Простейшие вероятностные задачи. Самостоятельная работа | 5 | 5 |
| 21 | Экспериментальные данные и вероятности событий | 4 | 4 |
| | Контрольная работа № 6 | 1 | 1 |
| VI. Итоговое повторение
| 21 | 18 |
|
|
| Итоговая контрольная работа за 1 полугодие | 0 | 1 |
|
|
| Итоговая контрольная работа | 1 | 1 |
|
| Итого: |
| 136 | 136 |
|
В рабочую программу внесены следующие изменения:
Из итогового повторения были добавлены по 1 часу на:
В 9 классе обучается 13 человек. Состав класса не однородный:
3 ученика (23%) имеют высокие результаты;
30 % обучающихся в данном классе имеют низкий уровень подготовки (ребята не умеют переключаться с одного вида деятельности на другой, плохо развиты навыки самостоятельной работы, работают в медленном темпе).
Поэтому учебным планом школы на 2014 -2015 учебный год на изучение алгебры в 9 классе выделен дополнительно 1 час из школьного компонента, что способствует расширению и углублению знаний и умений, а также развитию способностей, математического мышления, интересов сильных учащихся по предмету, и отработку навыков у слабых учеников, также подготовки выпускников к сдаче экзамена за курс основной школы в форме ГИА.
Данная программа составлена с учетом требований к математической подготовке учащихся и соответствует требованиям государственной программы.
Общая характеристика учебного процесса.
Учебный процесс осуществляется в классно – урочной форме в виде комбинированных, контрольно-проверочных и др. типов уроков. При организации учебного процесса будет обеспечена последовательность изучения учебного материала: новые знания опираются на недавно пройденный материал; обеспечено поэтапное раскрытие тем с последующей их реализацией.
Ведущими методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, частично-поисковый, проектно-исследовательский.
(рассказ; объяснение, лекция, беседа, применение наглядных пособий; дифференцированные задания, самостоятельная работа; взаимопроверка, самопроверка, дидактическая игра; решение проблемно-поисковых задач).
Формы организации учебного процесса: индивидуальные, групповые, фронтальные, индивидуально-групповые.
Конкретные формы организации обучения по ведущим целям:
Формирование знаний: лекция, конференция.
Формирование умений и навыков: практикум, деловая игра, тренинг.
Закрепление и систематизация знаний: семинар, соревнования.
Проверка знаний: самостоятельная работа, математический диктант, контрольная работа.
Формы организации учебной деятельности учащихся носят индивидуальный характер, предусмотрена работа в парах, работа в малых группах. Временные рамки решения многих задач не ограничиваются одним уроком и допускают разные уровни достижения. Для отработки и проверки знаний запланированы уроки с применением ИКТ (математические диктанты, тестовый контроль, устный счет, объяснение нового материала). Для дифференцированного подхода к учащимся используются разноуровневые контрольные работы, домашние проверочные работы для учащихся.
Основные типы уроков:
урок изучения нового учебного материала;
урок закрепления и применения знаний;
урок обобщающего повторения и систематизации знаний;
урок контроля знаний и умений.
Основным типом урока является комбинированный.
Повторение на уроках проводится в следующих видах и формах:
повторение и контроль теоретического материала;
разбор и анализ домашнего задания;
устный счет;
математический диктант;
индивидуальные задания по карточкам;
Формы контроля: текущий и итоговый.
Текущий контроль проводится с целью проверки усвоения изучаемого и проверяемого программного материала; содержание определяются учителем с учетом степени сложности изучаемого материала.
Используются следующие формы и методы контроля усвоения материала: устный контроль (индивидуальный опрос, устная проверка знаний); письменный контроль (контрольные работы, графические диктанты, тесты), проверка домашнего задания.
Формой промежуточной и итоговой аттестации являются: контрольная работа; проверочная работа; самостоятельная работа; диктант; тест.
Для итогового контроля составлены итоговые контрольные работы.
Контрольные работы составлены по крупным блокам материала или главам учебника, есть итоговая контрольная работа. В каждой работе по 5-6 заданий, первые три из них соответствуют уровню обязательной подготовки, последние задания по уровню сложности более продвинутые. На выполнение контрольной работы отводится 40-45 минут
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему результатов обучения, которых должны достичь все учащиеся, оканчивающие 7 класс. Эти требования структурированы по трём компонентам: знать, уметь, использовать приобретённые знания и умения в практической деятельности и повседневной жизни.
Механизмы формирования ключевых компетенций учащихся.
Программа предполагает, что успех формирования компетенций определяется рядом условий:
настроенностью учащихся на необходимость определенных действий
четкостью и доступностью изложения цели и задач, которые уч-ся должны решать в ходе учебной деятельности
полнотой и ясностью представления о структуре формируемого умения, показом учителем способов выполнения той или иной работы
организацией деятельности учащихся по овладению отдельными действиями или их совокупностью с использованием системы задач
применение деятельностного подхода обучения
Требования к уровню подготовки выпускников.
В результате изучения ученик должен:
знать/понимать:
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения; примеры их применения при решении математических и практических задач;
как математически определённые функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Арифметика
уметь:
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить из одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты – в виде дроби и дробь – в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь:
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять арифметические действия с алгебраическими дробями с одинаковыми и разными знаменателями;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение на множители; выполнять тождественные преобразования;
применять свойства арифметических квадратных корней для вычисления значений и осуществлять преобразования выражений, содержащих операцию извлечения квадратного корня;
решать линейные, квадратные и рациональные уравнения, сводящиеся к ним;
решать системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать задания, содержащие модуль числа;
оперировать с выражениями, содержащими степень с отрицательным целым показателем;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой; определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем,
строить и читать графики функций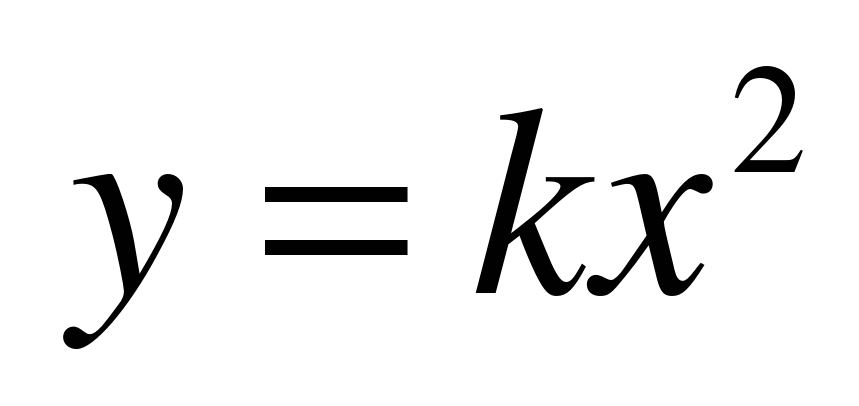 
, 
, 
;
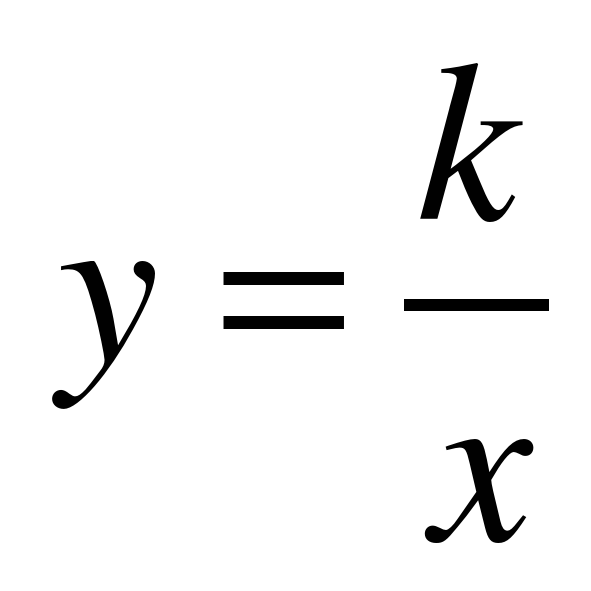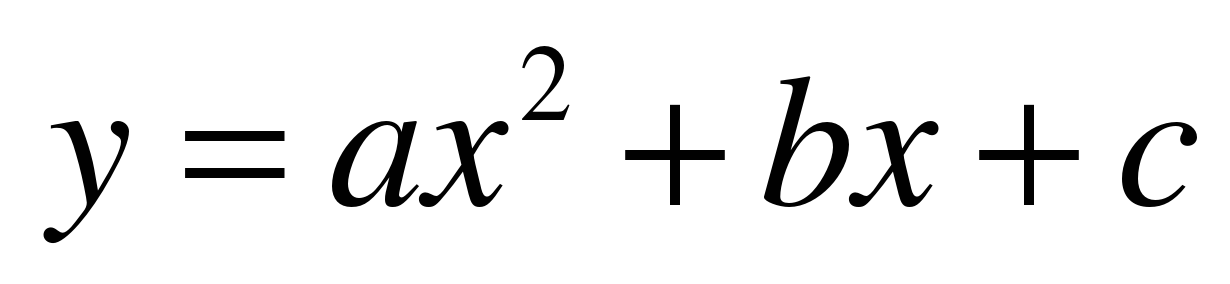строить и читать графики функций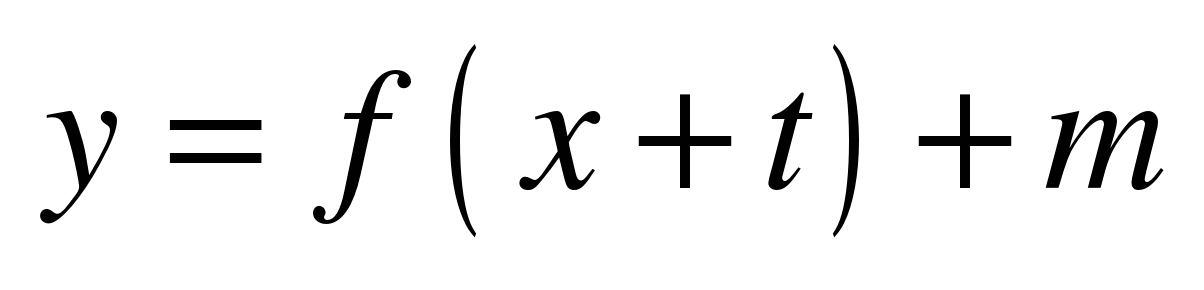 
на основе графика функции 
;
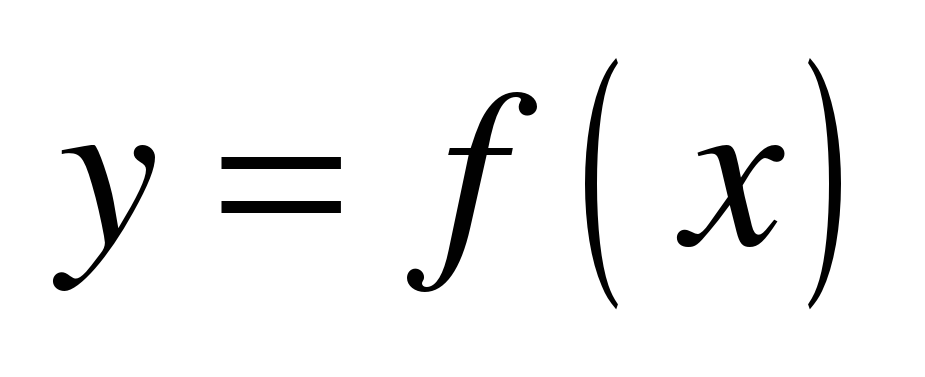строить график функции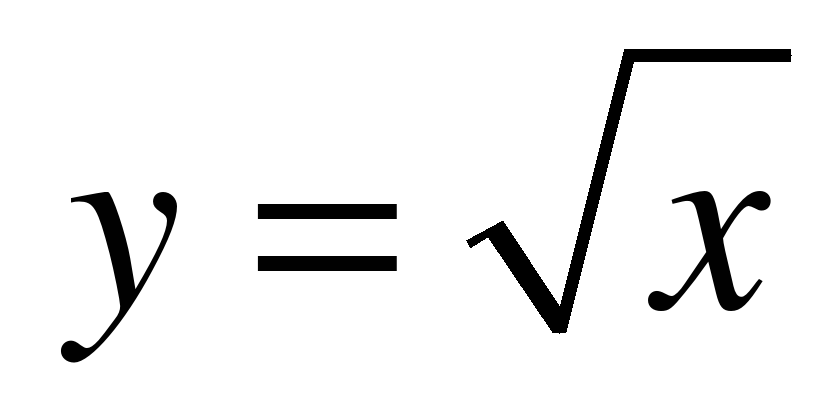 
;
исследовать функцию на монотонность.
строить графики изученных функций;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчётов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами;
Элементы логики, комбинаторики, статистики и теории вероятностей
уметь:
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
распознавать логически некорректных рассуждений;
решать учебные и практические задачи, требующих систематического перебора вариантов;
сравнивать шансы наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путём систематического перебора возможных вариантов, а также с использованием правила умножения;
вычислять средние значения результатов измерений; находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, оценке вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Обоснование выбора УМК, на основе которого ведется преподавание предмета.
Для обучения в 7-11 классах выбрана содержательная линия А.Г.Мордковича, рассчитанная на 5 лет. В девятом классе реализуется третий год обучения. Выбранный учебник входит в логически завершенную линию алгебры А.Г.Мордковича и является логическим продолжением курса алгебры в 8 классе. Автором учебника А.Г.Мордкович разработано тематическое планирование, рассчитанное на 4 часа в неделю (136 часов в год).
Учебно-методическое и информационное обеспечение курса
Состав учебно - методического комплекта:
Литература:
Для учителя
1. Александрова Л.А. Алгебра. 9 класс. Контрольные работы для учащихся общеобразовательных учреждений /Под ред. А.Г. Мордковича.
2. Александрова Л.А. Алгебра. 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений /Под ред. А.Г. Мордковича.
3. Государственный стандарт основного общего образования по математике.
4. Мордкович А.Г. Алгебра.7-9 кл.: Методическое пособие для учителя.
5. Программы. Математика. 5-6 классы. Алгебра. 7 – 9 классы. Алгебра и начала анализа. 10 – 11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович.
6. Интерактивная математика. 5-9. //Электронное учебное пособие для основной школы/ - «ДОС», 2003. «Дрофа», 2003.
7. Ким Е.А. Алгебра. 9 класс. Поурочные планы (по учебнику А.Г.Мордковича)/Авт.- сост.Е.А. Ким.
8. Лысенко Ф.Ф.. Подготовка к итоговой аттестации.
9. Математика, 5-11 классы. Практикум. //Учебное электронное издание.
10. Математика. 5-9 классы: развернутое тематическое планирование. Базовый уровень. Линия И. И. Зубаревой, А. Г.Мордковича
11. А. Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина. Алгебра. 9 класс.Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина.
12. А. Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина.. Алгебра. 9 класс. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович.
13. Мордкович А.Г., П. В. Семенов. События. Вероятности. Статистическая обработка данных. 7-9 классы: дополнительные главы к курсу алгебры для общеобразовательных учреждений.
14. Мордкович А.Г., Тульчинская Е.Е. Алгебра: Тесты для 7- 9 кл. общеобразовательных учреждений. – 2-е изд.
15. Мордкович А.Г. Алгебра.7-9 кл.: Методическое пособие для учителя.
16. Примерная программа основного общего образования по математике.
Список литературы для учащихся:
1. А. Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина. Алгебра. 9 класс. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина.
2. А. Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина.. Алгебра. 9 класс. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович.
3. Александрова Л.А. Алгебра. 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений /Под ред. А.Г. Мордковича.
4. Лысенко Ф.Ф.. Подготовка к итоговой аттестации. Издательство «Легион».
6.Мордкович А.Г., Тульчинская Е.Е. Алгебра: Тесты для 7- 9 кл. общеобразовательных учреждений.
Информационно-компьютерная поддержка учебного процесса
Для информационно-компьютерной поддержки учебного процесса предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:
Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет – ресурсов:
Министерство образования РФ: http://www.informika.ru/; http://www.ed.gov.ru/; http://www.edu.ru/.
Тестирование online: 5–11 классы: http://www.kokch.kts.ru/cdo/.
Педагогическая мастерская, уроки в Интернет и многое другое: http://teacher.fio.ru, http://www.zavuch.info/, http://festival.1september.ru, http://school-collection.edu.ru, http://www.it-n.ru, http://www.prosv.ru., www.mioo.ru, www.math.ru
Новые технологии в образовании: http://edu.secna.ru/main/.
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru.
Сайты «Мир энциклопедий»:
http://www.rubricon.ru/; http://www.encyclopedia.ru; http://ru.wiktionary.org
Критерии и нормы оценки знаний, умений и навыков
обучающихся по алгебре.
Учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
Среди погрешностей выделяются ошибки и недочеты.
Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.
Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Оценка ответа учащихся при устном и письменном опросе производится по пятибалльной системе.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им задания.
Итоговые отметки (за тему, четверть, курс) выставляются по состоянию знаний на конец этапа обучения с учетом текущих отметок.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя.
Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).
имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных контрольных работ учащихся.
Отметка «5» ставится в следующих случаях:
работа выполнена полностью.
в логических рассуждениях и обоснованиях нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
Отметка «3» ставится, если:
Отметка «2» ставится, если:
| Тесты «5» - 96-100% «4» - 75 -95% «3» - 60- 94% «2» - менее 60%.
| Устно (по карточкам) «5» - правильные ответы на все вопросы. «4» - на основной вопрос ответ верный, но на дополнительные не ответил или допустил ошибку. «3» - затруднился, дал не полный ответ, отвечал на доп. вопросы. «2» - не знает ответ и на дополнительные вопросы отвечает с трудом. |
Тексты контрольных работ
22
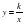. Функция 
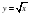. Свойства квадратного корня
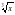,её свойства и график. 
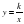. Функция 
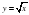. Свойства квадратного корня
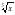,её свойства и график. 
