| № п/п | Тема урока | Элементы содержания урока | Тип урока | Требования к уровню подготовки обучающихся | Дополнительные знания, умения (требования повышенного уровня) |
|
| Повторение (5 часов) |
|
| Совместные действия над обыкновенными и десятичными дробями | Основное свойство дроби, арифметические действия над обыкновенными дробями, арифметические действия над десятичными дробями | Комбинированный | Уметь выполнять действия умножения и деления обыкновенных дробей, умножения смешанных чисел, деления числа на обыкновенную дробь. | Умение решать уравнения и задачи различного уровня сложности с помощью смешанных дробей. |
|
| Решение задач с помощью уравнений | Задачи на составление уравнений, задачи на проценты, задачи на пропорцию, задачи на движение | Комбинированный | Уметь записать и решить уравнение к задаче, в которой величины обратно пропорциональны; Уметь решать задачи на составление уравнений, на движение;
| Уметь решать наиболее рациональным способом задачи на составление уравнений, на проценты, на пропорцию, на движение, выполнять и оформлять тестовые задания, подбирать аргументы для обоснования найденной ошибки |
|
| Входной контроль | Индивидуальное решение контрольных заданий | Урок контроля, оценки и коррекции знаний
| Уметь обобщать и систематизировать знания оп основным темам курса математики 6 класса | Уметь обобщать и систематизировать знания оп основным темам курса математики 6 класса, решая задачи повышенной сложности |
|
| Математический язык. Математическая модель (13 часов) |
|
| Основная цель: | Формирование представлений о целостности и непрерывности курса математики 5 и 6 класса. Обобщить и систематизировать знания о числовых выражениях, о допустимых и недопустимых значениях переменной выражения, о математических утверждений, о математическом языке; о выполнении действий, по арифметическим законам сложения и умножения, действия с десятичными дробями, действия с обыкновенными дробями. Овладение навыками решения задач, составляя математическую модель реальной ситуации. Развитие логического, математического мышления и интуиции, творческих способностей в области математики. |
|
| Числовые и алгебраические выражения | числовые выражения, значение числового выражения, значение алгебраического выражения, допустимые и недопустимые значения переменной, алгебраические выражения, порядок выполнения действий, арифметические законы сложения и умножения, действия с десятичными дробями, действия с обыкновенными дробями. | Комбинированный | Знают понятия: числовое выражение, алгебраическое выражение, значение выражения, переменная, допустимое и недопустимое значение переменной. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. | Умеют находить значение числового выражения значение алгебраического выражения при заданных значениях переменных. Воспроизведение прослушанной и прочитанной информации с заданной степенью свернутости. Подбор аргументов для объяснения решения, участие в диалоге. |
|
| Комбинированный | Умеют находить значение алгебраического выражения при заданных значениях переменных. Восприятие устной речи, проведение информационно-смыслового анализа текста и лекции, приведение и разбор примеров. | Умеют находить значение алгебраического выражения при заданных значениях переменных рациональным способом. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
| Частично-поисковый | Умеют определять значения переменных, при которых имеет смысл выражение. Участие в диалоге, отражение в письменной форме своих решений, работа с математическим справочником, формирование умения выполнения и оформления тестовых заданий. | Учащиеся умеют определять, какие значения переменных для данного выражения являются допустимыми, недопустимыми; делают вывод о том, имеет ли смысл данное числовое выражение. Умеют участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение. |
|
| Что такое математический язык | математическое буквенное выражение, математические утверждения, математический язык. | Комбинированный
| Знают понятие математического языка. Умеют осуществлять «перевод» выражений с математического языка на обычный язык и обратно. Могут дать оценку информации, фактам, процессам, определять их актуальность. | Учащиеся умеют «переводить» математические правила, законы в символическую форму, осуществлять «обратный перевод». Могут самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. |
|
| Частично-поисковый |
|
| Что такое математическая модель | математическая модель, реальные ситуации, словесная модель, алгебраическая модель, графическая модель, геометрическая модель. | Проблемное изложение | Знают понятие математической модели. Умеют составлять математическую модель реальной ситуации, используя математический язык. Поиск нескольких способов решения, аргументация рационального способа, проведение доказательных рассуждений. | Умеют решать текстовые задачи, используя метод математического моделирования. Воспроизведение теории прослушанной с заданной степенью свернутости, участие в диалоге, подбор аргументов для объяснения ошибки. |
|
| Проблемный
| Умеют решать текстовые задачи, выделяя три этапа математического моделирования. Адекватное восприятие устной речи, проведение информационно-смыслового анализа текста, приведение примеров. | Используют для познания окружающего мира различные методы (наблюдение, измерение, моделирование). Восприятие устной речи, участие в диалоге, формирование умения составлять и оформлять таблицы, приведение примеров. |
|
| Поисковый |
|
| Линейное уравнение с одной переменной | Уравнение с одной переменной, уравнение с одной неизвестной, решения уравнения, корень уравнения, решить уравнение, равносильные уравнения, линейное уравнение с одной перемнной, стандарнтый вид уравнения | Комбинированный | Учащиеся знают понятие линейного уравнения и числа его корней Воспроизведение теории прослушанной с заданной степенью свернутости, участие в диалоге, подбор аргументов для объяснения ошибки. Учащиеся умеют определять, является ли пара чисел решением линейного уравнения с одной неизвестной. Восприятие устной речи, участие в диалоге, запись главного, приведение примеров. | Учащиеся понимают, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики. Восприятие устной речи, участие в диалоге, формирование умения составлять и оформлять таблицы, приведение примеров. Могут работать с тестовыми заданиями. |
|
| Проблемный |
|
| Координатная прямая | координатная прямая, координатная ось, координаты точки, модуль числа, открытый луч, числовой луч, интервал, полуинтервал, отрезок, числовые промежутки. |
Комбинированный
| Имеют представление о координатной прямой, о координатах точки, о модуле числа, о числовых промежутках. Составление алгоритмов, отражение в письменной форме результатов деятельности, могут заполнять математические кроссворды. | Умеют отмечать на координатной прямой точку с заданной координатой, определять координату точки; определять вид промежутка. Отражение в письменной форме своих решений, могут пользовать чертежными инструментами, рассуждать и обобщать, аргументировано отвечать на вопросы собеседников. |
|
| Проблемный |
|
| Контрольная работа № 1 по теме: «Математический язык» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение обобщения и систематизации знаний по основным темам курса математики 6 класса. Владение умением предвидеть возможные последствия своих действий. | Учащиеся могут свободно пользоваться умением обобщения и систематизации знаний по задачам повышенной сложности. Владение навыками контроля и оценки своей деятельности. |
|
Линейная функция (11 часов) |
|
|
Формирование представлений о прямоугольной системе координат, об абсциссе, ординате, о числовых промежутках, о числовых лучах, о линейной функции и ее графике. Формирование умений построения графика линейной функции, исследования взаимного расположение графиков линейных Функций. Овладение умением применения алгоритма отыскания координат точки, заданной в прямоугольной системе координат, алгоритма построения точки в прямоугольной системе координат, алгоритма построения графика линейного уравнения 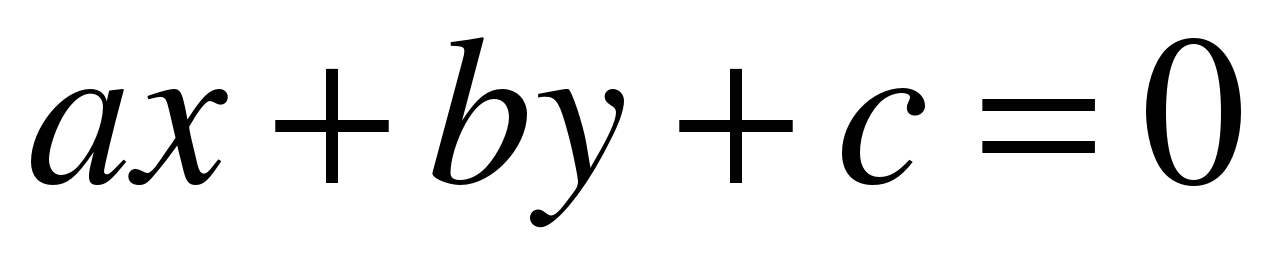 Овладение навыками решения линейного уравнения с двумя переменными 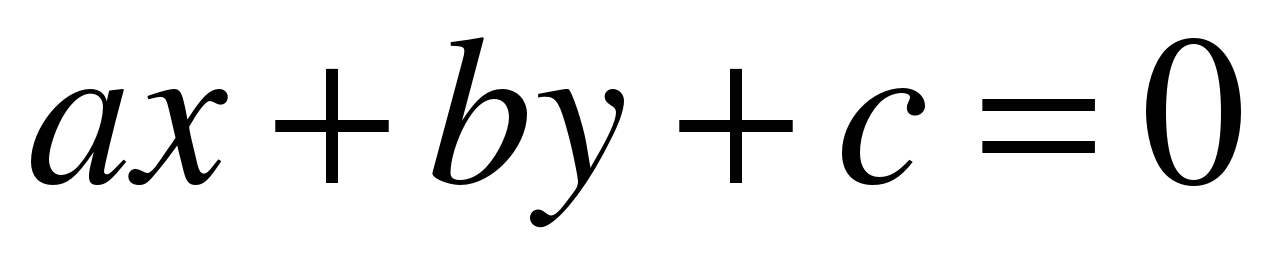 . . |
|
| Координатная плоскость | ПДСК, начало координат, координатная плоскость, оси координат, координатные углы, абсцисса, ордината, ось абсцисс, ось ординат, алгоритм отыскания координат точки, заданной в прямоугольной системе координат, алгоритм построения точки в прямоугольной системе координат. | Поисковый | Имеют представление о координатной прямой, о координатах точки, о модуле числа, о числовых промежутках. Составление алгоритмов, отражение в письменной форме результатов деятельности, могут заполнять математические кроссворды. (Р) Умеют отмечать на координатной прямой точку с заданной координатой, определять координату точки; определять вид промежутка. Воспроизведение изученной информации с заданной степенью свернутости, подбор формул, соответствующих решению, могут работать по заданному алгоритму. | Учащиеся умеют связывать геометрическую и аналитическую модели промежутка и выбирать адекватное обозначение и символическую запись. Могут, аргументировано отвечать ан поставленные вопросы, правильного оформления решений, аргументировать ошибки, участие в диалоге. Умеют проводить самооценку собственных действий. |
|
| Координатная плоскость |
| Комбинированный | Знают понятия: координатная плоскость, координаты точки. Умеют находить координаты точки на плоскости, отмечать точку с заданными координатами, используя алгоритм построения точки в прямоугольной системе координат. Умеют, аргументировано отвечать на поставленные вопросы, участие в диалоге. | Могут по координатам точки определяют её положение без построения, не производя построения, могут определить, в каком координатном угле расположена точка. Восприятие устной речи, проведение информационно-смыслового анализа текста и лекции, приведение и разбор примеров. Могут выделить и записать главное, могут привести примеры. |
|
| Линейное уравнение с двумя переменными и его график | линейное уравнение с одной переменной, линейное уравнение с двумя переменными, решение уравнения 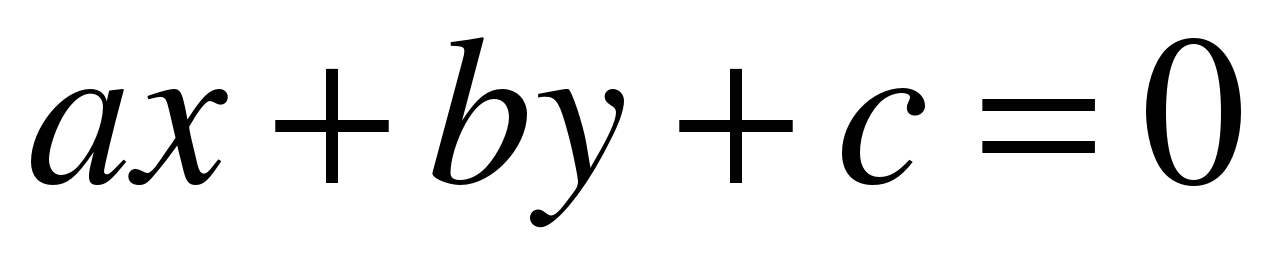 , бесконечно много решений, график уравнения, геометрическая модель, алгоритм построения графика уравнения , бесконечно много решений, график уравнения, геометрическая модель, алгоритм построения графика уравнения | Проблемный | Имеют представление о линейном уравнении с двумя переменными, о решения уравнения ax + by + c = 0, о графике уравнения. Воспроизведение теории прослушанной с заданной степенью свернутости, участие в диалоге, подбор аргументов для объяснения ошибки. | Учащиеся умеют составлять линейное уравнение по заданному корню. Могут на координатной плоскости строить график уравнения. Восприятие устной речи, участие в диалоге, формирование умения составлять и оформлять таблицы, приведение примеров. Могут работать с тестовыми заданиями. |
|
| Линейное уравнение с двумя переменными и его график |
| Комбинированный | Учащиеся умеют определять, является ли пара чисел решением линейного уравнения с двумя неизвестными, строить график уравнения ax + by + c = 0. Восприятие устной речи, участие в диалоге, запись главного, приведение примеров. | Учащиеся умеют находить корень линейного уравнения с двумя переменными, удовлетворяющий заданным условиям. Воспроизведение прослушанной и прочитанной информации с заданной степенью свернутости. |
|
| Линейное уравнение с двумя переменными и его график |
| Поисковый | Учащиеся умеют находить точку пересечения графиков линейных уравнений без построения, выражать в линейном уравнении одну переменную через другую. Формирование умения заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц. | Учащиеся умеют связывать словесную, алгебраическую и геометрическую модели реальной ситуации. Проведение информационно-смыслового анализа текста, выбор главного и основного, приведение примеров, формирование умения работать с чертежными инструментами. (И) |
|
| Линейная функция и ее график | линейная функция, независимая переменная, зависимая переменная, график линейной функции, знак принадлежности, наибольшее значение линейной функции на отрезке, наименьшее значение функции на отрезке, возрастающая линейная функция, убывающая линейная функция. | Комбинированный | Знают понятия: линейная функция, независимая переменная (аргумент), зависимая переменная, график линейной функции. Умеют по формуле определять характер монотонности. Формирование умения заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц. | Умеют преобразовывать линейное уравнение к виду линейной функции 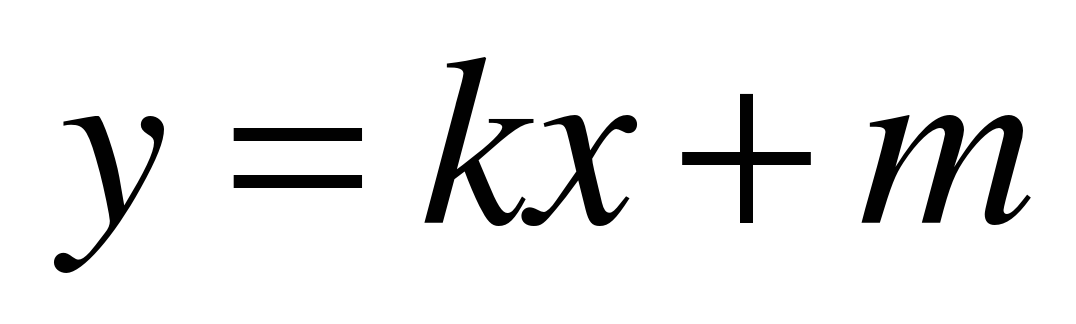 , находить значение функции при заданном значении аргумента, находить значение аргумента при заданном значении функции, строить график линейной функции. Умеют выполнять и оформлять задания программированного контроля. , находить значение функции при заданном значении аргумента, находить значение аргумента при заданном значении функции, строить график линейной функции. Умеют выполнять и оформлять задания программированного контроля. |
|
| Линейная функция и ее график | линейная функция, независимая переменная, зависимая переменная, график линейной функции, знак принадлежности, наибольшее значение линейной функции на отрезке, наименьшее значение функции на отрезке, возрастающая линейная функция, убывающая линейная функция. | Учебный практикум | Умеют преобразовывать линейное уравнение к виду линейной функции 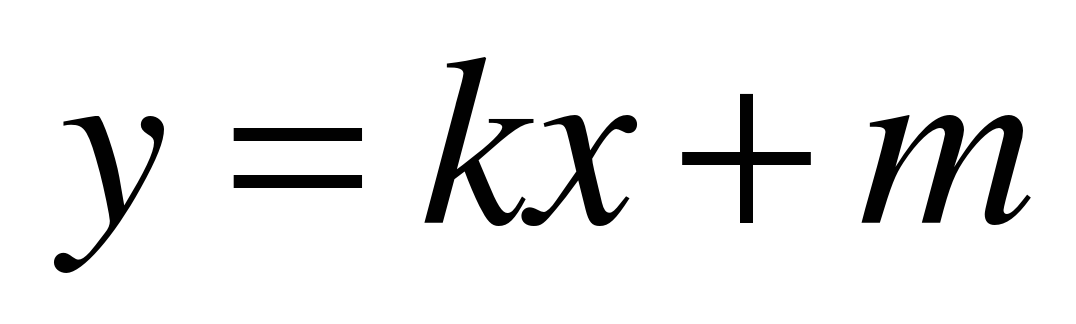 , находить значение функции при заданном значении аргумента, находить значение аргумента при заданном значении функции, строить график линейной функции. Могут излагать информацию, обосновывая свой собственный подход. , находить значение функции при заданном значении аргумента, находить значение аргумента при заданном значении функции, строить график линейной функции. Могут излагать информацию, обосновывая свой собственный подход. | Могут решить линейное неравенство, с помощью графика функции 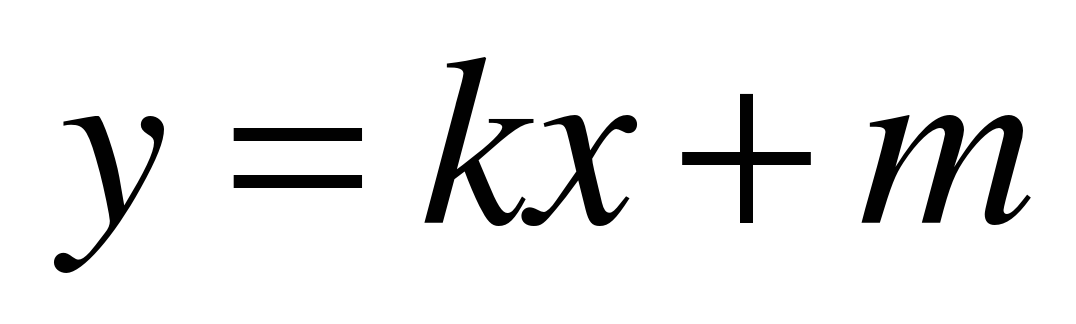 . Могут определить знаки коэффициентов . Могут определить знаки коэффициентов 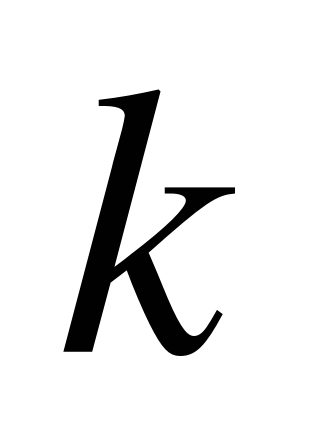 и и 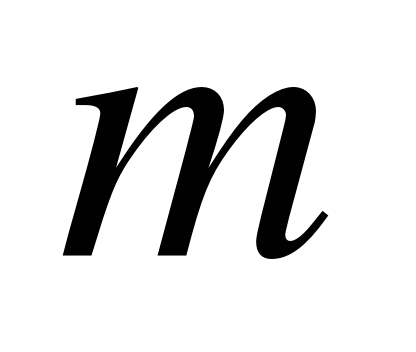 , если известно через какие четверти проходит график. Участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров. , если известно через какие четверти проходит график. Участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров. |
|
| Линейная функция и ее график | Поисковый | Умеют находить координаты точек пересечения графика с координатными осями, координаты точки пересечения графиков двух линейных функций, наибольшее и наименьшее значения функции на заданном промежутке. Умеют участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение. | Могут приводить примеры реальных ситуаций, математическими моделями которых являются линейные функции. Проведение информационно-смыслового анализа текста, выбор главного и основного, приведение примеров, формирование умения работать с чертежными инструментами. Могут найти и устранить причины возникших трудностей. |
|
| Линейная функция y = kx | прямая пропорциональность, коэффициент пропорциональности, график прямой пропорциональности, угловой коэффициент, график линейной функции. | Комбинированный | Знают понятия прямой пропорциональности, коэффициента пропорциональности, углового коэффициента. Умеют находить коэффициент пропорциональности, строить график функции 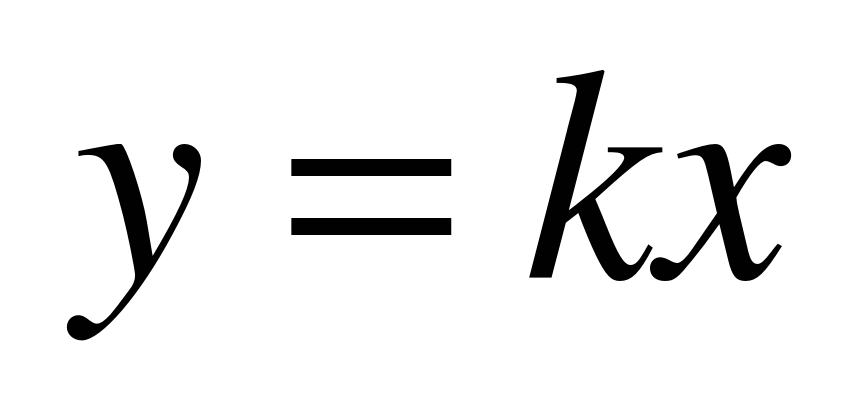 . Умеют определять знак углового коэффициента по графику. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. . Умеют определять знак углового коэффициента по графику. Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. | Умеют доказывать, что графиком прямой пропорциональности является прямая линия. Умеют по графику составлять уравнение прямой линии. Восприятие устной речи, участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров. Могут привести примеры, подобрать аргументы, сформулировать выводы. |
|
| Взаимное расположение графиков линейных функций | графики линейных функций параллельны, графики линейных функций пересекаются, алгебраическое условие параллельности и пересечения графиков линейных функций. | Комбинированный | Умеют определять взаимное расположение графиков по виду линейных функций. Воспроизведение прочитанной информации с заданной степенью свернутости, формирование умения работать по заданному алгоритму. | Могут находить неизвестные компоненты линейных функций, если задано взаимное расположение их графиков. Составление алгоритмов, отражение в письменной форме результатов деятельности, умеют заполнять математические кроссворды. |
|
| Контрольная работа № 2 по теме: «Линейная функция» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение расширять и обобщать знания о построения графика линейной функции, исследования взаимного расположение графиков линейных функций. | Могут самостоятельно выбрать рациональный способ решения линейного уравнения с двумя переменными 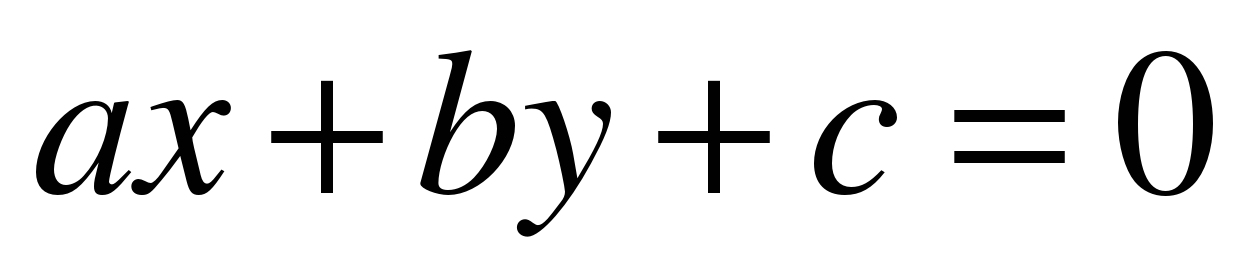 . Владение навыками контроля и оценки своей деятельности. . Владение навыками контроля и оценки своей деятельности. |
|
Системы двух линейных уравнений с двумя переменными (13 часов) |
|
| Формирование представлений о системе двух линейных уравнений с двумя переменными, о несовместности системы, о неопределенной системе уравнении. Овладение умением решения систем линейных уравнений графическим методом, методом подстановки и методом алгебраического сложения. Овладение навыками составления математической модели реальных ситуации в виде системы двух линейных уравнений с двумя переменными. |
|
| Основные понятия
| система уравнений, решение системы уравнений, графический метод решения системы, система несовместима, система неопределенна. | Комбинированный | Знают понятия система уравнений, решения системы уравнений. Умеют определять, является ли пара чисел решением системы уравнений, решать систему линейных уравнений графическим способом. Могут самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | Уверенно владеют понятиями несовместной системы, неопределённой системы. Способны объяснить, почему система не имеет решений, имеет единственное решение, имеет бесконечное множество решений. Осуществляют проверку выводов, положений, закономерностей, теорем. |
|
|
| Учебный практикум | Могут решить графически систему уравнений. Способны объяснить, почему система не имеет решений, имеет единственное решение, имеет бесконечное множество решений. Умеют добывать информацию по заданной теме в источниках различного типа. | Могут к каждому уравнению подобрать второе так, чтобы полученная система не имела решений, имела единственное решение, имела бесконечно много решений. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. |
|
| Метод подстановки | метод подстановки, система двух уравнений с двумя переменными, алгоритм решения системы двух уравнений с двумя переменными методом подстановки. | Комбинированный | Знают алгоритм решения системы линейных уравнений методом подстановки. Умеют решать системы двух линейных уравнений методом подстановки по алгоритму Используют для решения познавательных задач справочную литературу. | Умеют решать системы двух линейных уравнений методом подстановки. Восприятие устной речи, участие в диалоге, умеют, аргументировано отвечать, приведение примеров. Умеют работать по заданному алгоритму, аргументировать ответ или ошибку. |
|
| Учебный практикум | Могут решать системы двух линейных уравнений методом подстановки. Могут выбрать и выполнить задание по своим силам и знаниям, применить знания для решения практических задач. | Могут решать системы двух линейных уравнений методом подстановки, выбирая наиболее рациональный путь Умеют, аргументировано отвечать на поставленные вопросы, участие в диалоге. |
|
| Поисковый | Умеют составлять математическую модель реальной ситуации в виде системы линейных уравнений. Могут отделить основную информацию от второстепенной информации. | Могут уверенно составлять математическую модель реальной ситуации в виде системы линейных уравнений и решать ее. Умеют определять понятия, приводить доказательства. |
|
| Метод алгебраического сложения | система двух уравнений с двумя переменными, метод алгебраического сложения. | Комбинированный | Знают алгоритм решения системы линейных уравнений методом алгебраического сложения. Умеют решать системы двух линейных уравнений методом подстановки по алгоритму. Умеют проводить сравнительный анализ, сопоставлять, рассуждать. | Умеют решать системы двух линейных уравнений методом алгебраического сложения. Проведение информационно-смыслового анализа прочитанного текста, умеют пользоваться справочником для нахождения формул. |
|
|
Метод алгебраического сложения |
| Учебный практикум | Могут решать системы двух линейных уравнений методом алгебраического сложения. Могут проводить анализ данного задания, аргументировать решение, презентовать решения. | Могут решать системы двух линейных уравнений алгебраического сложения, выбирая наиболее рациональный путь. Воспроизведение правил и примеров, могут работать по заданному алгоритму. |
|
|
Метод алгебраического сложения |
| Поисковый | Могут решать системы двух линейных уравнений алгебраического сложения, выбирая наиболее рациональный путь. Отражение в письменной форме своих решений, могут рассуждать и обобщать, участие в диалоге, выступать с решением проблемы. | Учащиеся умеют решать системы линейных уравнений, выбирая наиболее рациональный в данной ситуации метод Подбор аргументов, соответствующих решению, участие в диалоге, могут проводить сравнительный анализ. Умеют формировать вопросы, задачи, создавать проблемную ситуацию. |
|
| Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций | составление математической модели реальной ситуации, система двух линейных уравнений с двумя переменными. | Комбинированный | Имеют представление о системе двух линейных уравнений с двумя переменными. Знают, как составить математическую модель реальной ситуации. Могут выделить и записать главное, могут привести примеры. | Умеют решать текстовые задачи с помощью системы линейных уравнений. Воспроизведение изученной информации с заданной степенью свернутости, подбор аргументов, соответствующих решению, могут правильно оформлять работу. |
|
| Проблемный | Умеют решать текстовые задачи с помощью системы линейных уравнений на движение по дороги и реке. Проведение информационно-смыслового анализа прочитанного текста, составление конспекта, участие в диалоге. | Умеют решать текстовые задачи с помощью системы линейных уравнений на движение по дороги и реке, на части, на числовые величины и проценты. Отражение в письменной форме своих решений, формирование умения рассуждать. |
|
| Частично-поисковый
| Умеют решать текстовые задачи с помощью системы линейных уравнений на части, на числовые величины и проценты. Воспроизведение изученной информации с заданной степенью свернутости, могут работать по заданному алгоритму и правильно оформлять работу. | Умеют решать системы линейных уравнений, выбирая наиболее рациональный путь, умеют решать текстовые задачи повышенного уровня трудности. Участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, составление конспекта, приведение примеров. |
|
|
Учебный практикум
|
|
| Контрольная работа № 3 по теме: «Системы двух линейных уравнений с двумя переменными» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение расширять и обобщать знания о решении систем линейных уравнений графическим методом, методом подстановки и методом алгебраического сложения. | Могут самостоятельно выбрать рациональный способ составления математической модели реальных ситуации в виде системы двух линейных уравнений с двумя переменными. |
|
| Степень с натуральным показателем и ее свойства ( 6 часов) |
|
| Основная цель: | Формирование представлений о степени с натуральным показателем, о степени с нулевым показателем. Формирование умений составления таблицы основных степеней и применение ее при решении заданий. Овладение умением применения свойств степени с натуральным показателем при решении задач, выполнять действие умножение и деление степеней с одинаковыми показателями. Овладение навыками решения уравнений, содержащих степень с натуральным показателем. |
|
| Что такое степень с натуральным показателем | степень с натуральным показателем, степень, основание степени, показатель степени, возведение в степень, четная степень, нечетная степень. | Комбинированный | Знают понятия: степень, основание степени, показатель степени. Умеют возводить числа в степень. Формирование умения заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц. | Умеют находить значения сложных выражений со степенями, представлять число в виде произведения степеней. Проведение информационно-смыслового анализа прочитанного текста, участие в диалоге, приведение примеров.
|
|
| Таблицы основных степеней | степени числа 2, степени числа 3, степени числа 5, степени числа 7, степени составных чисел. | Проблемный | Умеют пользоваться таблицей степеней при выполнении вычислений со степенями. Участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров. | Умеют пользоваться таблицей степеней при выполнении заданий повышенной сложности. Проведение информационно-смыслового анализа текста, выбор главного и основного, приведение примеров, формирование умения работать с чертежными инструментами. |
|
| Свойства степени с натуральным показателем | свойства степеней, доказательство свойств степеней, теорема, условие, заключение. | Комбинированный | Знают правила умножения и деления степеней с одинаковыми основаниями, правило возведения степени в степень. Осуществляют проверку выводов, положений, закономерностей, теорем. | Умеют выводить свойства степени с натуральным показателем, применять их для упрощения выражений со степенями. Умеют добывать информацию по заданной теме в источниках различного типа. |
|
| Поисковый | Умеют применять свойства степеней для упрощения числовых и алгебраических выражений. Могут, аргументировано отвечать на поставленные вопросы, могут осмыслить ошибки и их устранить. Умеют, развернуто обосновывать суждения. | Умеют применять свойства степеней для упрощения сложных алгебраических дробей. Восприятие устной речи, участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров. |
|
| Умножение и деление степеней с одинаковым показателем | степени с разными основаниями, действия с степенями одинакового показателя. | Комбинированный | Знают правила умножения и деления степеней с одинаковыми показателями. Знают, как применять эти правила при вычислениях, для преобразования алгебраических выражений. Умеют определять понятия, приводить доказательства. | Умеют выводить формулы произведения и частного степеней одинаковыми показателями, применять их для упрощения вычислений со степенями. Восприятие устной речи, участие в диалоге, запись главного, приведение примеров. |
|
| Степень нулевым показателем | степень с натуральным показателем, степень с нулевым показателем | Проблемный | Могут находить степень с натуральным показателем. Умеют находить степень с нулевым показателем. Формирование умение работать по заданному алгоритму, доказывать правильность решения с помощью аргументов. | Могут аргументировано обосновать равенство а0 = 1. Умеют находить значения сложных выражений с нулевыми степенями. Составление алгоритмов, отражение в письменной форме результатов деятельности, умеют заполнять математические кроссворды. |
|
| Одночлены. Арифметические операции над одночленами (8 часов) |
|
| Основная цель: | Формирование представлений об одночлене стандартного вида, об арифметических операциях над одночленами, о подобных одно Умеют, развернуто обосновывать суждения членах. Формирование умений представлять одночлен в стандартном виде, выполнять арифметические действия над одночленами. Овладение умением складывать, вычитать, умножать и делить одночлены, а также возводить одночлен в степень Овладение навыками решения задач на составление уравнений, предполагающих приведение подобных слагаемых |
|
| Понятие одночлена. Стандартный вид одночлена | одночлен, стандартный вид одночлена, коэффициент одночлена. | Комбинированный | Знают понятия: одночлен, коэффициент одночлена, стандартный вид одночлена. Умеют находить значение одночлена при указанных значениях переменных. Умеют вступать в речевое общение, участвовать в диалоге. | Умеют приводить к стандартному виду сложные одночлены. Умеют работать по заданному алгоритму, выполнять и оформлять тестовые задания, сопоставлять предмет и окружающий мир. Умеют решать проблемные задачи и ситуации. |
|
| Сложение и вычитание одночленов | подобные одночлены, метод введения новой переменной, алгоритм сложения (вычитания) одночленов | Комбинированный | Знают понятие подобных одночленов, алгоритм сложения (вычитания) одночленов. Воспроизведение прочитанной информации с заданной степенью свернутости, формирование умение правильного оформления решений, умение выбрать из данной информации нужную информацию. | Умеют выполнять сложение и вычитание одночленов, приводя их стандартному виду. Владение диалогической речью, подбор аргументов, формулировка выводов, отражение в письменной форме результатов своей деятельности. Могут отделить основную информацию от второстепенной информации. |
|
| Проблемное изложение | Умеют применять правила сложения и вычитания одночленов для упрощения выражений и решения уравнений. Воспроизведение изученной информации с заданной степенью свернутости, подбор аргументов, соответствующих решению, формирование умения правильно оформлять работу. | Умеют применять правила сложения и вычитания одночленов для упрощения выражений и решения уравнений. Отражение в письменной форме своих решений, формирование умения сопоставлять и классифицировать, участвовать в диалоге. Умеют выполнять и оформлять задания программированного контроля. |
|
| Умножение одночленов. Возведение одночлена в натуральную степень | умножение одночленов, возведение одночлена в натуральную степень, корректная задача, некорректная задача. | Проблемное изложение | Знают алгоритм умножения одночленов и возведения одночлена в натуральную степень. Проведение информационно-смыслового анализа прочитанного текста, составление конспекта, участие в диалоге. | Умеют выполнять умножение и возведение в степень сложных одночленов. Проведение информационно-смыслового анализа прочитанного текста, умеют пользоваться справочником для нахождения формул. |
|
| Умножение одночленов. Возведение одночлена в натуральную степень | умножение одночленов, возведение одночлена в натуральную степень, корректная задача, некорректная задача. | Комбинированный
| Могут применять правила умножения одночленов, возведения одночлена в степень для упрощения выражений. Воспроизведение изученной информации с заданной степенью свернутости, подбор аргументов, соответствующих решению, могут правильно оформлять работу. | Могут свободно представлять данный одночлен в виде степени одночлена, оперируют понятиями «корректная задача», «некорректная задача». Восприятие устной речи, участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров. |
|
| Деление одночлена на одночлен | деление одночлена на одночлен, стандартный вид делителя и делимого, алгоритм деления одночлена на одночлен. | Комбинированный
| Знают алгоритм деления одночленов. Умеют выполнять деление одночленов по алгоритму. Могут применять правило деления одночленов для упрощения алгебраических дробей. | Могут выполнить деление сложных одночленов. Могут делать вывод о корректности операции деления данных одночленов. |
|
| Комбинированный |
|
| Контрольная работа №4 по теме: «Одночлены. Арифметические операции над одночленами» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение расширять и обобщать об арифметических операциях над одночленами. Владение умением предвидеть возможные последствия своих действий. | Могут самостоятельно выбрать рациональный способ решения задач на составление уравнений, приведение подобных слагаемых. Владеют навыками самоанализа и самоконтроля. |
|
| Итоговая контрольная работа за 1 полугодие |
| Урок контроля, оценки |
| |
|
| Многочлены. Арифметические операции над многочленами (15 часов) |
|
| Основная цель: | Формирование представлений о многочлене, о приведение подобных членов многочлена, о стандартном виде многочлена, о формулах сокращенного умножения. Формирование умений представлять многочлен в стандартном виде, выполнять арифметические действия над многочленами. Овладение умением складывать, вычитать, умножать и делить многочлены, вывода и применения формул сокращенного умножения. Овладение навыками решения уравнений, предполагающих применение формул сокращенного умножения. |
|
| Основные понятия | многочлен, члены многочлена, приведение подобных членов многочлена, стандартный вид многочлена, полином. | Проблемное изложение | Имеют представление о многочлене, о действие приведения подобных членов многочлена, о стандартном виде многочлена, о полиноме. Могут приводить сложный многочлен к стандартному виду и находить, при каких значениях переменной он равен 1. Формировать умение выбрать и выполнить задание по своим силам и знаниям, применить знания для решения практических задач. | . Могут приводить сложный многочлен к стандартному виду и записывать его члены в порядке убывания степеней переменной. Восприятие устной речи, проведение информационно-смыслового анализа лекции, составление конспекта, приведение и разбор примеров. Умеют, развернуто обосновывать суждения. |
|
| Сложение и вычитание многочленов | сложение и вычитание многочленов, взаимное уничтожение слагаемых, алгебраическая сумма многочленов, правила составления алгебраической суммы многочленов. |
Комбинированный
| Знают правило составления алгебраической суммы многочленов. Умеют выполнять сложение и вычитание многочленов. Восприятие устной речи, проведение информационно-смыслового анализа лекции, приведение и разбор примеров, участие в диалоге. | Могут выполнять сложение и вычитание многочленов, преобразуя а многочлен стандартного вида, решать уравнения. Участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, составление конспекта, приведение примеров. |
|
| Проблемное изложение |
|
| Умножение многочлена на одночлен | умножение многочлена на одночлен, распределительный закон умножения, вынесение общего множителя за скобки. | Комбинированный | Имеют представление о распределительном законе умножения, о вынесение общего множителя за скобки, об операции умножение многочлена на одночлен. Отражение в письменной форме своих решений, формирование умения рассуждать, выступать с решением проблемы. | Могут применять правило умножения многочлена на одночлен для упрощения выражений, решения уравнений. Восприятие устной речи, проведение информационно-смыслового анализа текста и лекции, составление конспекта, приведение и разбор примеров. Используют для решения познавательных задач справочную литературу. |
|
| Проблемное изложение | Умеют выполнять умножение многочлена на одночлен выносить за скобки одночленный множитель. Отражение в письменной форме своих решений, могут рассуждать и обобщать, участие в диалоге, выступать с решением проблемы. | Учащиеся умеют решать текстовые задачи, используя полученные знания по теме. Могут выполнять и оформлять тестовые задания, подбор аргументов для обоснования найденной ошибки. Могут составлять конспект, проводить сравнительный анализ, сопоставлять, рассуждать. |
|
| Умножение многочлена на многочлен | раскрытие скобок, умножение многочлена на многочлен. | Поисковый | Знают правило умножения многочленов. Умеют выполнять умножение многочленов. Восприятие устной речи, участие в диалоге, могут, аргументировано рассуждать и обобщать, приведение примеров. | Умеют решать текстовые задачи, математическая модель которых содержит произведение многочленов. Проведение информационно-смыслового анализа прочитанного текста, составление конспекта, могут сопоставлять и классифицировать. |
|
| Практикум | Умеют решать текстовые задачи, математическая модель которых содержит произведение многочленов. Могут рассуждать и обобщать, подбор аргументов, соответствующих решению, участие в диалоге. | Могут решать текстовые задачи, выделяя три этапа математического моделирования. Могут решать уравнение, в которых, при упрощении выражения умножаются многочлены. Могут работать с тестовыми заданиями. |
|
| Урок закрепления изученного материала | Учащихся демонстрируют умение расширять и обобщать знания о сложении, вычитании, умножении и делении многочленов. Владение умением предвидеть возможные последствия своих действий. | Могут самостоятельно выбрать рациональный способ решения уравнений, выполнять арифметические действия над многочленами. Владение навыками контроля и оценки своей деятельности |
|
| Формулы сокращенного умножения | квадрат суммы, квадрат разности, разность квадратов, разность кубов, сумма кубов. | Комбинированный | Имеют представление о формулах квадрата суммы и разности, разности квадратов и кубов, сумма кубов. Имеют представление о геометрическом обосновании этих формул. | Могут выводить формулы квадрата суммы и разности, разности квадратов и кубов, сумма кубов. Понимают геометрическое обоснование этих формул. Умеют выполнять преобразования многочленов по формулам. |
|
| Поисковый | Знают, как выполнять преобразования многочленов, вычисления по формулам квадрата суммы и разности, разности квадратов и кубов, сумма кубов. Могут проводить анализ данного задания, аргументировать решение, презентовать решения. | Умеют выполнять преобразования многочленов, вычисления по формулам квадрата суммы и разности, разности квадратов и кубов, сумма кубов. Восприятие устной речи, участие в диалоге, подбор аргументов для ответа на поставленный вопрос, приведение примеров. Отражение в письменной форме своих решений, умение вести диалог. |
|
| Проблемный | Умеют выполнять преобразования многочленов, вычисления по формулам квадрата суммы и разности, разности квадратов и кубов, сумма кубов. |
|
| Исследовательский
| Умеют применять формулы сокращённого умножения для упрощения выражений, решения уравнений. Могут использовать данные правила и формулы, аргументировать решение, формирование умения правильно оформлять работу. | Могут свободно применять формулы сокращённого умножения для упрощения выражений, решения уравнений. Восприятие устной речи, участие в диалоге, умеют, аргументировано отвечать, приведение примеров. Умеют передавать, информацию сжато, полно, выборочно. |
|
| систематизация знаний |
|
| Деление многочлена на одночлен | свойство деления суммы на число, правило деления многочлена на одночлен. | Поисковый | Знают правило деления многочлена на одночлен. Умеют делить многочлен на одночлен. Воспроизведение изученной информации с заданной степенью свернутости, подбор аргументов, соответствующих решению, могут правильно оформлять работу. | Умеют делать вывод о корректности операции деления многочлена на одночлен, умеют выполнять деление многочлена на одночлен. Выполняют поиск неизвестных компонентов деления в сложных случаях. Могут пользовать математическим справочником, рассуждать и обобщать, выступать с решением проблемы, аргументировано отвечать на вопросы собеседников. |
|
| Контрольная работа № 5 по теме: «Многочлены. Арифметические операции над многочленами» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение расширять и обобщать знания о сложении, вычитании, умножении и делении многочленов, вывода и применения формул сокращенного умножения. Владение навыками контроля и оценки своей деятельности | Могут самостоятельно выбрать рациональный способ решения уравнений, предполагающих применение формул сокращенного умножения. Владение умением предвидеть возможные последствия своих действий. |
|
| Разложение многочлена на множители (20 ч) |
|
| Основная цель: | Формирование представлений о разложении многочлена на множители, об алгебраической дроби, о тождествах. Овладение умением вынесения общего множителя за скобки, группировки слагаемых, преобразовывать выражения, используя формулы сокращенного умножения, выделения полного квадрата. Овладение навыками решения уравнений, выделением полного квадрата, решение уравнений, применяя формулы сокращенного умножения. |
|
| Что такое разложение многочлена на множители и зачем оно нужно | разложить на множители, корни уравнения, сокращение дробей, разложение многочлена на множители. | Комбинированный | Имеют представление о корнях уравнения, о сокращение дробей, о разложение многочлена на множители. Подбор аргументов для доказательства своего решения, могут выполнять и оформлять тестовые задания. | Имеют чёткое представление об области применения операции разложения многочлена на множители. Могут решить уравнение и сократить дробь, разложив на множители. Ведение диалога, могут, аргументировано отвечать на поставленные вопросы. |
|
| Вынесение общего множителя за скобки | вынесение общего множителя за скобки, наибольший общий делитель коэффициентов, алгоритм отыскания общего множителя нескольких одночленов. | Поисковый | Знают алгоритм отыскания общего множителя нескольких одночленов. Умеют выполнять вынесение общего множителя за скобки по алгоритму. Могут рассуждать и обобщать, вести диалог, выступать с решением проблемы, аргументировано отвечать на вопросы собеседников. | Умеют выполнять вынесение за скобки общего многочленного множителя, владеют приёмом замены переменной. Отражение в письменной форме своих решений, формирование умения проводить сравнительный анализ пройденных тем. Могут собрать материал для сообщения по заданной теме. |
|
| Вынесение общего множителя за скобки | Комбинированный | Умеют применять приём вынесения общего множителя за скобки для упрощения вычислений, решения уравнений. Могут рассуждать, обобщать, видеть несколько решений одной задачи, выступать с решением проблемы, аргументировано отвечать на вопросы собеседников. | Могут свободно применять приём вынесения общего множителя за скобки для выполнения заданий повышенного уровня сложности. Участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, могут обобщать, приведение примеров.
|
|
| Способ группировки
| способ группировки, разложение на множители. | Комбинированный | Имеют представление об алгоритме разложения многочлена на множители способом группировки. Могут, аргументировано рассуждать, обобщать, участие в диалоге, понимание точки зрения собеседника, приведение примеров.
| Умеют выполнять разложение многочлена на множители способом группировки по алгоритму. Восприятие устной речи, проведение информационно-смыслового анализа прочитанного текста и лекции, приведение и разбор примеров, участие в диалоге.
|
|
| Поисковый
| Умеют выполнять разложение многочлена на множители способом группировки по алгоритму. Проведение информационно-смыслового анализа прочитанного текста, могут вычленять главное, участие в диалоге. | Учащиеся умеют применять способ группировки для упрощения вычислений. Восприятие устной речи, проведение информационно-смыслового лекции, составление конспекта, разбор примеров. Умеют работать по заданному алгоритму, аргументировать ответ или ошибку. |
|
|
| Обобщение и систематизация знаний |
|
| Разложение многочлена на множители с помощью формул сокращенного умножения.
| формулы сокращенного умножения, разложение на множители по формулам сокращенного умножения. | Комбинированный | Знают, как разложить многочлен на множители с помощью формул сокращенного умножения в простейших случаях. Воспроизведение изученной информации с заданной степенью свернутости, подбор аргументов, соответствующих решению, могут правильно оформлять работу. | Могут выполнять разложение многочлена на множители с помощью формул сокращенного умножения в простейших случаях. Отражение в письменной форме своих решений, могут рассуждать, выступать с решением проблемы, аргументировано отвечать на вопросы собеседников. |
|
| Учебный практикум | Умеют раскладывать любой многочлен на множители с помощью формул сокращенного умножения. Проведение информационно-смыслового анализа прочитанного текста, составление конспекта, могут работать с чертежными инструментами. | Учащиеся умеют выполнять разложение на множители с помощью формул сокращенного умножения для сложных многочленов. Воспроизведение изученных правил и понятий, подбор аргументов, соответствующих решению, могут работать с чертежными инструментами. |
|
| формулы сокращенного умножения, разложение на множители по формулам сокращенного умножения. | Проблемный | Умеют применять приём разложения на множители с помощью формул сокращённого умножения для упрощения вычислений и решения уравнений. Отражение в творческой работе своих знаний, могут сопоставлять окружающий мир и геометрические фигуры, рассуждать, выступать с решением проблемы. | Могут свободно применять разложение многочлена на множители с помощью формул сокращенного умножения для упрощения вычислений и решения уравнения. Могут рассуждать и обобщать, видеть применение знаний в практических ситуациях, выступать с решением проблемы |
|
| Разложение многочлена на множители с помощью формул сокращенного умножения.
|
|
Исследовательский
| Могут свободно применять разложение многочлена на множители с помощью формул сокращенного умножения для упрощения вычислений и решения уравнения. Восприятие устной речи, проведение информационно-смыслового анализа лекции, могут работать с чертежными инструментами. | Учащиеся умеют применять приём разложения на множители с помощью формул сокращённого умножения для выполнения заданий повышенного уровня сложности. |
|
|
| Комбинированный |
|
| Разложение многочлена на множители с помощью комбинации различных приемов | разложение на множители, вынесение за скобки общего множителя, формулы сокращенного умножения, способ группировки, метод введения полного квадрата. | Проблемный | Имеют представление о комбинированных приёмах, разложения на множители: вынесение за скобки общего множителя, формулы сокращенного умножения, способ группировки, метод введения полного квадрата. | Умеют выполнять разложение многочленов на множители с помощью комбинации изученных приёмов. Восприятие устной речи, составление конспекта, вычленение главного, могут работать с чертежными инструментам. |
|
| Разложение многочлена на множители с помощью комбинации различных приемов | разложение на множители, вынесение за скобки общего множителя, формулы сокращенного умножения, способ группировки, метод введения полного квадрата. | Поисковый | Умеют выполнять разложение многочленов на множители с помощью комбинации изученных приёмов. Воспроизведение правил и примеров, могут работать по заданному алгоритму.
| Учащиеся умеют применять разложение многочлена на множители с помощью комбинации различных приёмов для упрощения вычислений, решения уравнений. Умеют формулировать полученные результаты. |
|
| Обобщение знаний |
|
| Сокращение алгебраических дробей
| алгебраическая дробь, числитель алгебраической дроби, знаменатель алгебраической дроби, сокращение алгебраических дробей. | Комбинированный | Имеют представление об алгебраической дроби, числителе и знаменателе алгебраической дроби, о сокращение алгебраических дробей. Могут рассуждать, аргументировать, обобщать, выступать с решением проблемы, умение вести диалог. | Могут сокращать алгебраические дроби, раскладывая выражения на множители, применяя формулы сокращенного умножения. Могут правильно оформлять работу, аргументировать свое решение, умения выбрать задания соответствующие знаниям. |
|
| Учебный практикум | Могут сокращать алгебраические дроби, раскладывая выражения на множители, применяя формулы сокращенного умножения. Отражение в письменной форме своих решений, формирование умения рассуждать, выступать с решением проблемы. | Умеют сокращать сложные алгебраические дроби, комбинируя изученные методы разложения многочленов на множители. Могут выполнять и оформлять тестовые задания, аргументировать решение и найденные ошибки, обобщать. |
|
|
Поисковый
| Умеют сокращать сложные алгебраические дроби, комбинируя изученные методы разложения многочленов на множители. Могут правильно оформлять работу, отражение в письменной форме своих решений, выступать с решением проблемы. | Могут решать уравнения и вычислять выражения, содержащие дробную форму записи. Могут классифицировать и проводить сравнительный анализ, рассуждать и обобщать, аргументировано отвечать на вопросы собеседников. (И) |
|
| Обобщение и систематизация знаний |
|
| Тождества | тождество, тождественно равные выражения, тождественные преобразования. | Комбинированный | Знают понятия тождества, тождественно равных выражений, тождественного преобразования. Умеют доказывать простейшие тождества. Могут рассуждать, обобщать, аргументировано отвечать на вопросы собеседников, вести диалог. | Умеют доказывать тождества, выполняя при этом тождественные преобразования алгебраических выражений. Отражение в творческой работе знаний плоских геометрических фигур, могут сопоставлять окружающий мир и геометрический фигуры, аргументировано отвечать на вопросы собеседников. |
|
| Контрольная работа № 6 по теме: «Разложение многочлена на множители» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение расширять и обобщать знания о вынесения общего множителя за скобки, группировки слагаемых, преобразовывать выражения, используя формулы сокращенного умножения, выделения полного квадрата. | Могут самостоятельно выбрать рациональный способ решения уравнений, выделением полного квадрата, решение уравнений, применяя формулы сокращенного умножения Владение умением предвидеть возможные последствия своих действий. |
|
| Функция 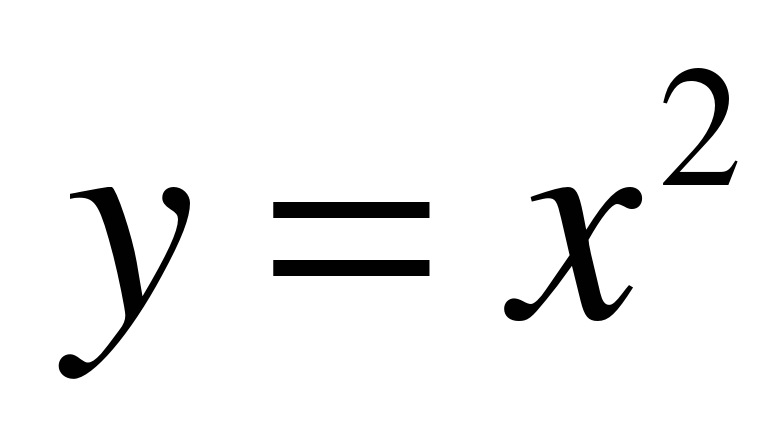 (9 часов) (9 часов) |
|
| Основная цель: | Формирование представлений о параболе, о вершине и фокусе параболы, о квадратичной функции и ее графике. Формирование умений построения графика квадратичной функции, определять участки возрастания и убывания функции, находить точки разрыва о область определения функции. Овладение умением описывать свойства функции по ее графику, чтения графика функции Овладение навыками построения графика кусочно-заданной функции, применения алгоритма графического решения уравнения. |
|
| Функция 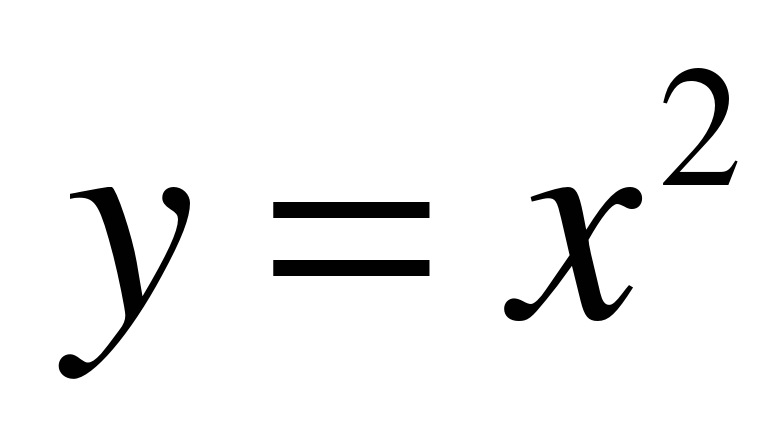 и ее график и ее график | парабола, ось симметрии параболы, ветви параболы, вершина параболы, фокус параболы, функция 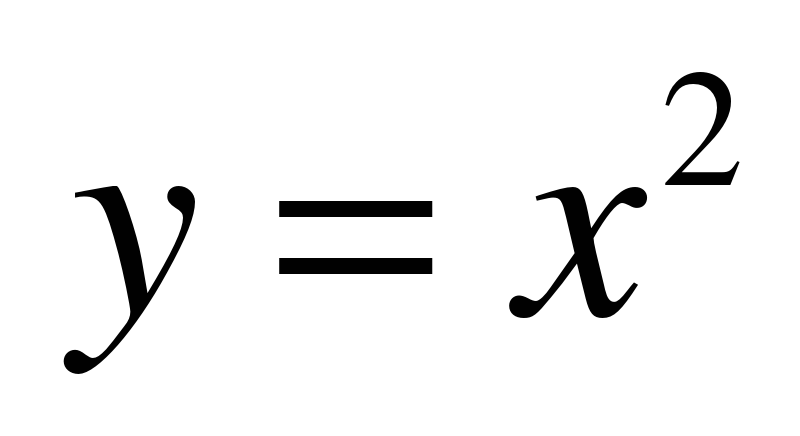 , график функции , график функции 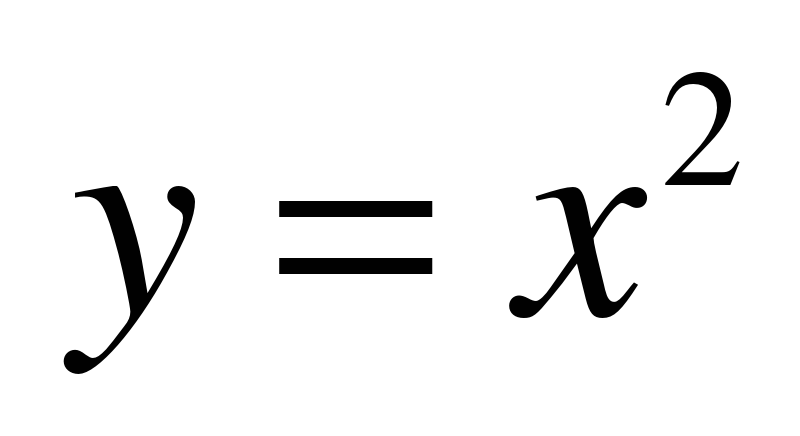 . . | Комбинированный | Знают понятия: парабола, ветви параболы, ось симметрии параболы, ветви параболы, вершина параболы. Умеют строить параболу. Умеют пользоваться энциклопедией, математическим справочником, записанными правилами. | Владеют навыками чтения графиков по готовому чертежу. Могут строить график на промежутке. Владение диалогической речью, подбор аргументов, формулировка выводов, отражение в письменной форме результатов своей деятельности. |
|
| Учебный практикум
| Умеют описывать геометрические свойства параболы, находить наибольшее и наименьшее значения функции y = x2 на заданном отрезке, точки пересечения параболы с графиком линейной функции. Умеют, аргументировано отвечать на поставленные вопросы, осмысление ошибок и их устранение. | Могут свободно читать графики функций. Могут сравнивать между собой наибольшие значения разных функций на промежутке. Воспроизведение изученной информации с заданной степенью свернутости, подбор аргументов, соответствующих решению, формирование умения правильно оформлять работу. |
|
| Поисковый |
|
| Графическое решение уравнений. | прямая, параллельная оси x , прямая, проходящая через начало координат, парабола, уравнение, график функции, пересечение графиков, графическое решение уравнения. | Комбинированный | Знают алгоритм графического решения уравнений. Знают, как выполнять решение уравнений графическим способом. Умеют работать по заданному алгоритму, выполнять и оформлять тестовые задания, сопоставлять предмет и окружающий мир. | Могут выполнять решение уравнений графическим способом. Воспроизведение прочитанной информации с заданной степенью свернутости, формирование умение правильного оформления решений, умение выбрать из данной информации нужную информацию. |
|
| Учебный практикум | Могут выполнять решение уравнений графическим способом. Восприятие устной речи, проведение информационно-смыслового анализа лекции, составление конспекта, приведение и разбор примеров. | Могут свободно решить сложные уравнения графическим способом. Восприятие устной речи, участие в диалоге, понимание точки зрения собеседника, подбор аргументов для ответа на поставленный вопрос, приведение примеров.
|
|
| Что означает в математике запись 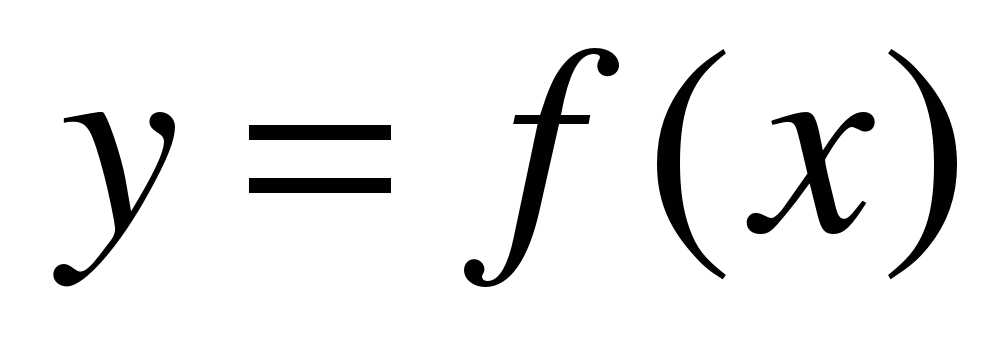 | выражение с переменной, значение выражения с переменной, функциональная запись выражения, кусочно-заданная функция, чтение графика, область определение функции, непрерывная функция, разрывная функция. | Комбинированный | Имеют представление о кусочно-заданной функции, об области определения функции, о непрерывной функции, о точке разрыва. Отражение в письменной форме своих решений, формирование умения сопоставлять и классифицировать, участвовать в диалоге. | Учащиеся имеют чёткое представление о кусочно-заданной функции, области определения, непрерывности функции, умеют оперировать функциональной символикой, использовать основные приемы чтения графика. Могут, аргументировано отвечать на поставленные вопросы, могут осмыслить ошибки и их устранить. |
|
| Комбинированный
| Умеют строить график кусочно-заданной функции, находить область определения функции. Могут по графику описывать геометрические свойства прямой, параболы. | Учащиеся умеют составлять аналитическую запись функции по её графику. Учащиеся умеют по графику описывать геометрические свойства прямой, параболы. |
|
| Поисковый |
|
| Контрольная работа №7 по теме: «Функция» |
| Урок контроля, оценки и коррекции знаний | Учащихся демонстрируют умение расширять и обобщать знания о построении графика квадратичной функции, нахождении участки возрастания и убывания функции, точек разрыва и области определения функции. | Могут сам-но выбрать рациональный способ построения графика кусочно-заданной функции, применения алгоритма графич. решения уравнения. Владение умением предвидеть возможные последствия своих действий. |
|
| Обобщающее повторение курса алгебры за 7 класс ( 2 ч) |
|
| Основная цель: | Обобщить и систематизировать курс алгебры за 7 класс, решая задания повышенной сложности. Формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни. |
|
| Степень с натуральным показателем и ее свойства.. Разложение многочлена на множители | Свойства степени с натуральным показателем, действия с степенями. Формулы сокращенного умножения, арифметические операции над многочленами, разложение многочленов на множители. | Комбинированный | Умеют применять свойства степеней для упрощения числовых и алгебраических выражений. Могут, аргументировано отвечать на поставленные вопросы, могут осмыслить ошибки и их устранить. Умеют применять формулы сокращённого умножения для упрощения выражений, решения уравнений. | Умеют применять свойства степеней для упрощения сложных алгебраических дробей. Могут свободно применять формулы сокращённого умножения для упрощения выражений, решения уравнений. |
|
| Линейная функция. Функция | Линейная функция, график функции, взаимное расположение графиков линейных функций. Функция 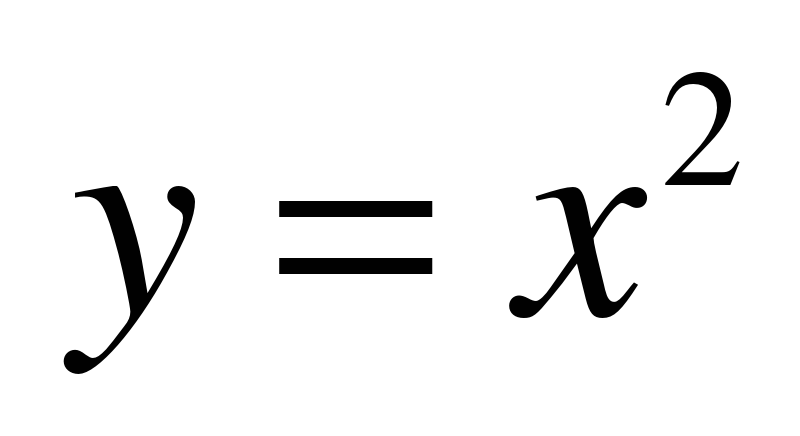 , график функции, графическое решение уравнения. , график функции, графическое решение уравнения. | Комбинированный | Умеют находить координаты точек пересечения графика с координатными осями, координаты точки пересечения графиков двух линейных функций, наибольшее и наименьшее значения функции на заданном промежутке. | Могут приводить примеры реальных ситуаций, математическими моделями которых являются линейные функции. Могут найти и устранить причины возникших трудностей. |
|
| Итоговая контрольная работа |
| Урок контроля, оценки знаний уч. |
|
|
|
 ана функция у =
ана функция у = 















