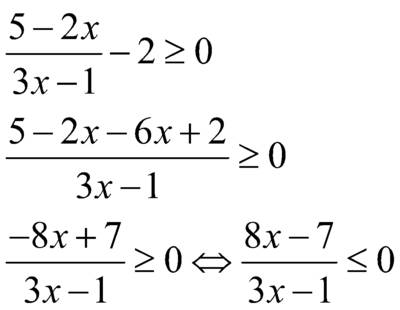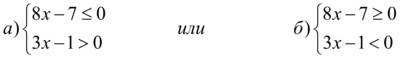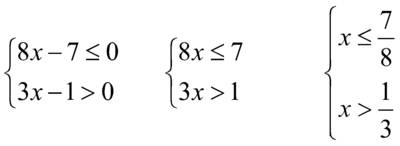Открытый урок "Уравнения и неравенства"

ное бюджетное профессиональное образовательное учреждение города Москвы

«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»

(ГБПОУ Юридический колледж)

ПЛАН-КОНСПЕКТ учебного занятия

по ОУДу.04 Математика

учебной дисциплине/междисциплинарному курсу

для обучающихся группа 108 курс 1

специальность 40.02.02 Правоохранительная деятельность

(набор 2019 г.)

(базовая подготовка)

дата проведения занятия по расписанию

                       пятница                                    26.06.2020                                                         1

                  день недели                                                         дата                                            номер пары

форма проведения дистанционно

преподаватель Н.В.Васильева

                                                                         фио преподавателя

Уравнения. Неравенства.

Цель занятия: повторение теоретического материала по теме: уравнения и неравенства.

Задачи занятия:

Обучающая: Основные приемы и методы решения задач по теме: уравнения и неравенства.

Воспитательная: воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов, формирование умения рационально, аккуратно оформить задание в тетради;

Развивающая: развивать умение обобщать, систематизировать на основе сравнения, развивать логическое мышление, исследовательские навыки, функционального мышления, математической речи.

 Базовый учебник: 

1. Алгебра и начала анализа: Учебник для 10-11 классов общеобразовательных учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю. В. Сидоров и др. М., Просвещение, 2019.

Дополнительная литература:

1. Башмаков М.И. Математика. М., «Академия», 2014

2.  Богомолов Н.В. Сборник задач (учебное пособие) – М.: Дрофа, 2015.

Интернет-ресурсы:

Междисциплинарные связи: алгебра и начала анализа, физика, естествознание

Внутридисциплинарные связи: геометрия.

УРАВНЕНИЯ  И НЕРАВЕНСТВА

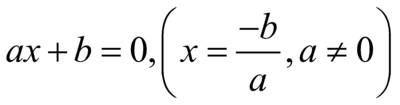 – линейное уравнение I степени с одной переменной

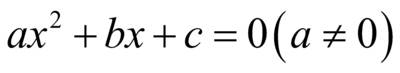 – уравнение II степени с одной переменной

Решить уравнение – значит найти множество его корней или доказать, что их нет. это множество называют решением уравнения. 

Два уравнения называются равносильными если решение (корень) одного уравнения является решением (корнем) другого уравнения и наоборот.

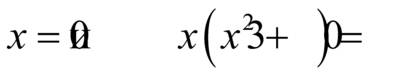Уравнения   равносильны, так как оба имеют единственный корень  .

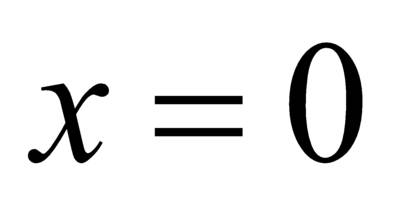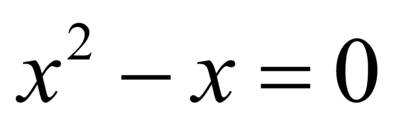Уравнения   и 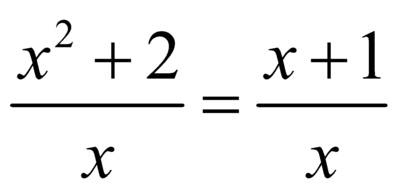  – неравносильны, так как   является корнем первого уравнения, но не удовлетворяет второму уравнению.

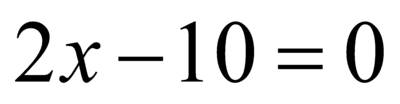Уравнения   и 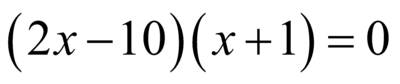  неравносильны, так как корень первого уравнения  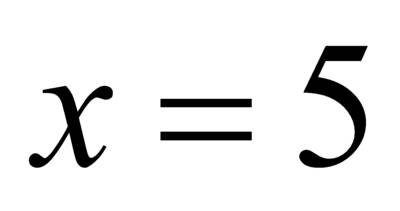, а второе уравнение кроме этого корня имеет еще корень  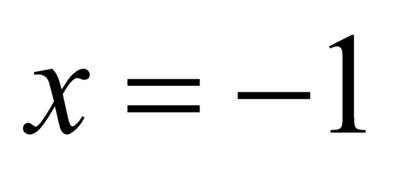, который не является корнем первого уравнения.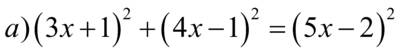

Решим уравнения:

раскроем скобки, применяя формулы сокращенного умножения   и 

приведем подобные члены, получим

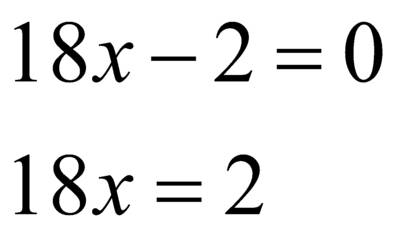
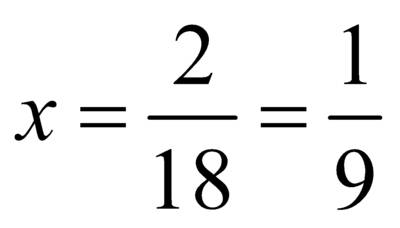                 Ответ:  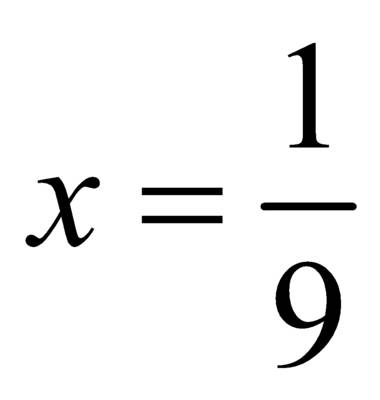 – корень уравнения.

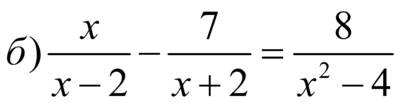 разложим  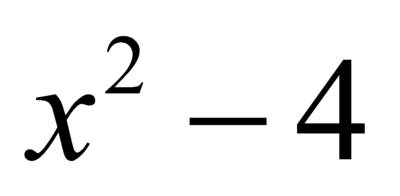 на множители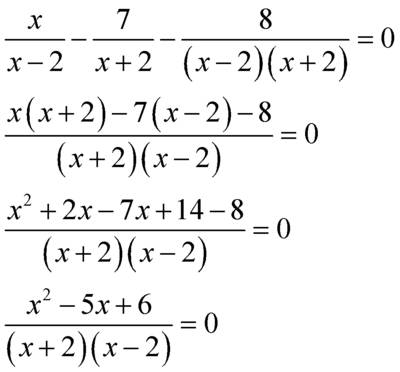

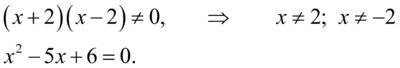
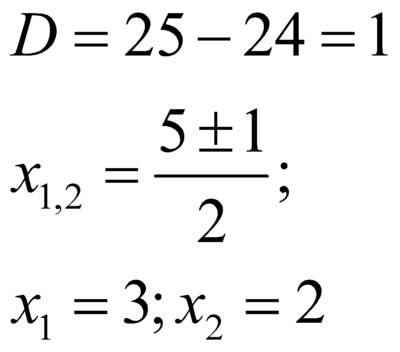перенесем все члены уравнения в левую часть и приведем дроби к общему знаменателю

дробь равна нулю, когда её числитель равен нулю, а знаменатель не равен нулю, т. е.

Решаем уравнение

 (корни можно найти по теореме Виета)

Так как   – посторонний корень и решением уравнения будет 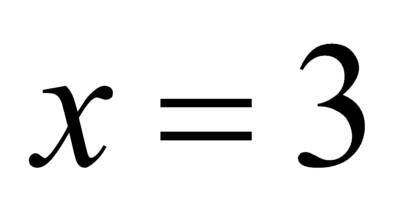 . Ответ:  .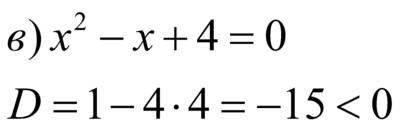

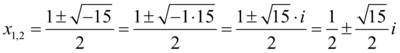уравнение не имеет действительных корней. Найдем мнимые корни.

 (мы знаем, что  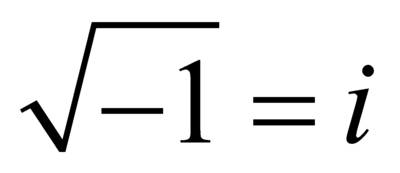 – мнимая единица)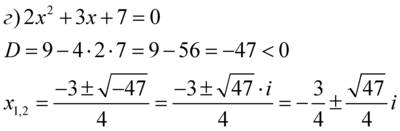

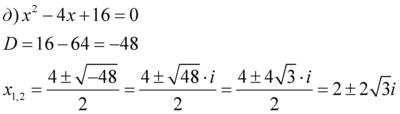
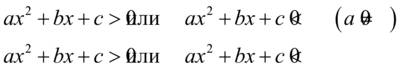 – неравенства I степени с одной переменной

 – неравенства II степени с одной переменной

Решить неравенство – значит найти множество значений переменной, при которых это неравенство является верным.

Два неравенства называются равносильными, если множество решений этих неравенств совпадают.

Решим неравенства

а) 

Перенесем все члены в левую часть и приведем к общему знаменателю. общий знаменатель 10; так как знаменатель не содержит переменной, то есть сразу видно что он не равен нулю, то в дальнейшем его можно не писать (опустить).

б) 

, то есть 

Используя свойства числовых неравенств, имеем

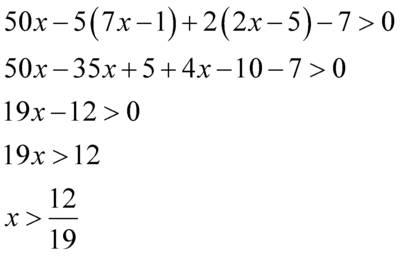
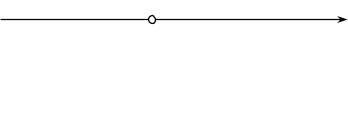
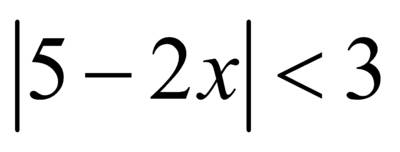
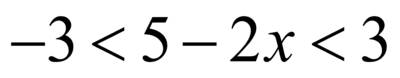
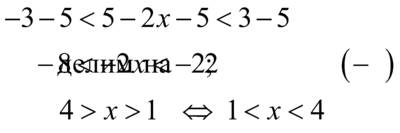, знак неравенства меняется на противоположный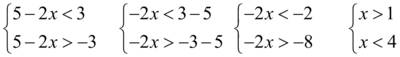

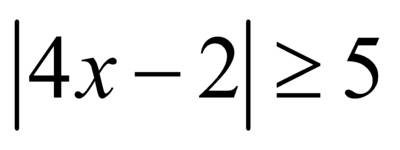
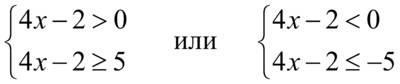
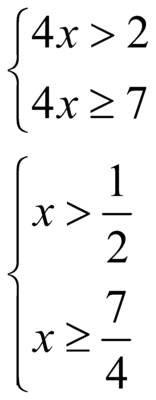
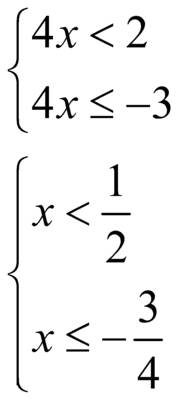
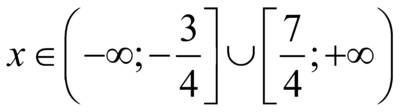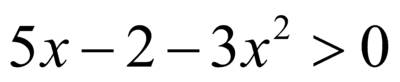
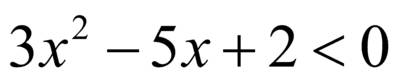
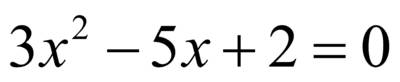
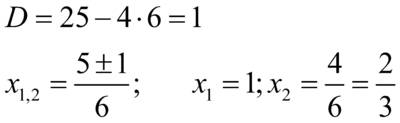
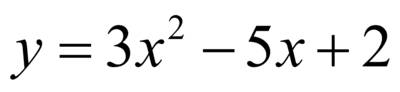Или можно записать в виде системы неравенств

в) 

Решаем две системы

Ответ:  .

г)   

умножим на (–1)

квадратное неравенство

Найдем корни уравнения 

Графиком функции   является парабола, ветви которой направлены вверх, а точки пересечения параболы и оси OX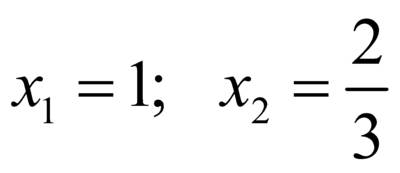 

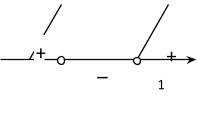
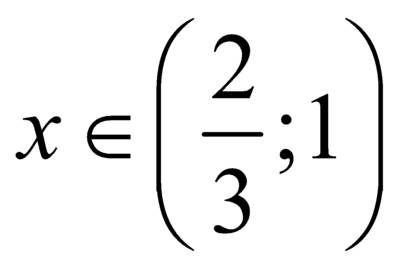
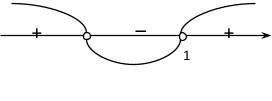
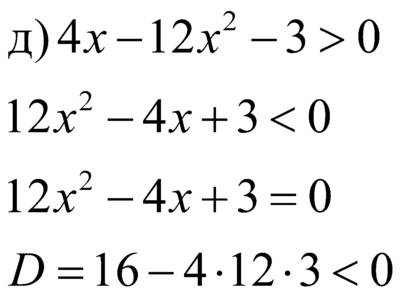
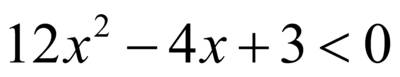Изобразим геометрически:

или

или

получаем три интервала, в которых определяем знак трехчлена. Так как мы решаем неравенство  , то решением неравенства будет промежуток (интервал) 

действительных корней нет, так как ветви параболы направлены вверх, то парабола не пересекает ось и расположена выше её, где всегда 0, 

а мы решаем неравенство  , значит данное неравенство не имеет решения.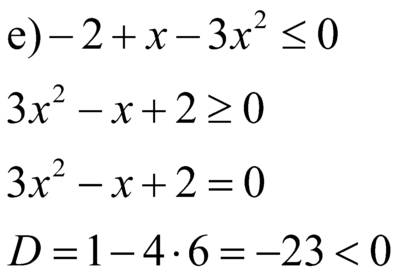

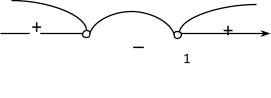
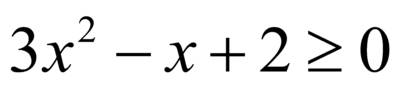уравнение не имеет действительных корней, т.е. парабола не пересекает ось, ветви параболы направлены вверх, 

а так как мы решаем неравенство  , то оно имеет множество решений, т.е.  .

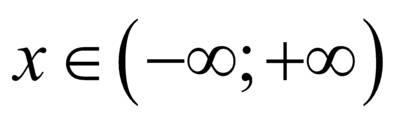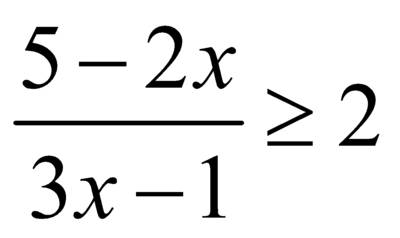ж)   – дробно–рациональное неравенство, которое может быть решено или через системы неравенств или методом интервалов. Перенесем правую часть в левую, приведем подобные члены

Решим через системы неравенств. Дробь

(Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю).

При решении системы неравенств надо решить каждое неравенство и выбрать общие промежутки.

Решаем