5 класс
Как люди научились считать.
Было время, когда человек был уже человеком, но считать еще не умел. Точнее, он знал только два числа: «один» и «много». Потом это «много» стало отодвигаться все дальше и дальше – появились числа «два», «три»… - но это было так медленно, что на каждое новое число уходили столетия, а то и тысячелетия!
Представьте себе: человек уже делал замечательные каменные орудия, западни для диких зверей, шил одежду из шкур, - и все это – проявляя чудеса изобретательности! А вот считать человек не умел. Почему?
Как ни странно, потому, что ему трудно было заметить сходство предметов! Считать ведь можно только предметы, похожие друг на друга, а первобытному человеку все казалось различным. Каждый человек его племени был для него особенным – с каждым его связывали свои особые отношения: ведь все племя было одной большой семьей. Каждый зверь убитый на охоте, тоже был единственным в своем роде – ведь каждая охота запоминалась надолго: она была настолько опасна, что могла стать последней. Вообще мир виделся первобытному человеку намного ярче, чем нам сегодня: даже деревья в лесу не казались ему одинаковыми – глаз его всегда искал, чем отличается одно дерево от другого (иначе легко было заблудиться и погибнуть).
Однако постепенно человек стал замечать сходство предметов, а когда люди стали обмениваться друг с другом, например менять шкуры зверей на каменные топоры, появилась и потребность в счете. Самый важный шаг был сделан, когда человек догадался заменить при счете одни предметы другими, более удобными, потому что они всегда под рукой, - например камешками или раковинами. И когда человек заметил, что у двух шкур и у двух камешков есть что-то общее, он сделал одно из величайших изобретений за всю человеческую историю: он изобрел число!
Со временем человек обнаружил, что удобнее всего пользоваться для счета предметами, которые есть на его руке, то есть пальцами. Так человек начал считать пятерками, десятками и двадцатками (в ход шли и пальцы ног!) Счет десятками сохранился и в нашей десятичной системе счисления. Остались и названия некоторых чисел, связанные с первой «вычислительной машиной» - пальцами рук и ног: например русское слово пять происходит от древнеславянского слова пясть – рука (вспомните слово запястье). А у некоторых племен число двадцать называлось весь человек!
Записывали числа поначалу очень просто: делали зарубки на куске дерева или кости (показать рисунок).
На этой кости тридцать тысяч лет назад сделаны нарезки – они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!
Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Со временем потребовались знаки для десятка десятков и так далее. Очень наглядной была система таких знаков у египтян:
(показать рисунок).
Несмотря на свою громоздкость, такая запись чисел была довольно удобной. Однако у нее был очень большой недостаток. Хотите знать какой? Попробуйте умножить или разделить два числа, записанных древнеегипетским способом!
Запись чисел, похожую на египетскую, использовали и древние римляне, только цифры у них были другими, и обозначались ими не только десятки, но и пятерки, например:
(показать рисунок).
Римскими цифрами иногда пользуются и сегодня: например, ими часто нумеруют главы в книгах. Однако, вычислять с помощью римских цифр так же неудобно, как и с помощью египетских.
Казалось бы, удобные цифры должны были изобрести греки, которые создали математику как науку. Однако вычислениями греки не увлекались и поэтому ограничились просто тем, что обозначили числа буквами своего алфавита. Так же, буквами, обозначались числа и в Древне Руси.
Те очень удобные числа, которыми мы пользуемся сегодня, изобрели индийцы: они так любили вычислять, что даже математические книги писали в стихах! (Представляете себе, насколько легче было бы выучить таблицу умножения, если бы она была записана стихами?) Индийцы догадались, что значение цифры может зависеть от ее места в записи числа
- именно благодаря этому оказалось возможным записывать все числа с помощью всего десяти цифр.
Индийские цифры так сильно упростили вычисления, что со временем завоевали весь мир. В Европу эти цифры попали благодаря арабам, поэтому индийские цифры называют арабскими.
До этого в Европе пользовались римскими цифрами. О том, насколько трудны были вычисления с этими цифрами, говорят слова одного европейского ученого, который жил около 700 года: «В мире есть много трудных вещей, но нет ничего труднее четырех действий арифметики!»
такая веревка была длиною в сто локтей).
Так записывали в Египте число
3246:
I – единица (тут римляне были неоригинальны).
V – пять ( считают, что этот знак произошел от изображенной руки).
X – десять (две руки).
L – пятьдесят.
C – сто.
D – пятьсот.
M – тысяча.
Число 36 римляне записывали так XXXVI
8 класс
О квадратных корнях.
С давних пор наряду с отысканием площади квадрата по известной длине его стороны приходилось решать и обратную задачу: «Какой должна быть сторона квадрата, чтобы его площадь равнялась а ? » Такую задачу умели решать еще 4 тыс. лет назад вавилонские ученые. Они составляли таблицы квадратов чисел и квадратных корней из чисел.
Вавилоняне использовали метод приближенного извлечения квадратного корня, который состоял в следующем. Пусть а – некоторое число (имеется в виду натуральное число), не являющееся полным квадратом. Представим а в виде суммы b2 + c. Где с достаточно мало по сравнению с b2 . Тогда
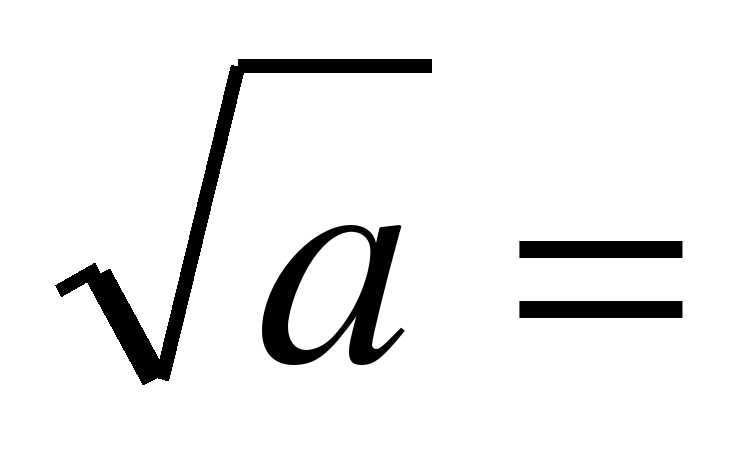
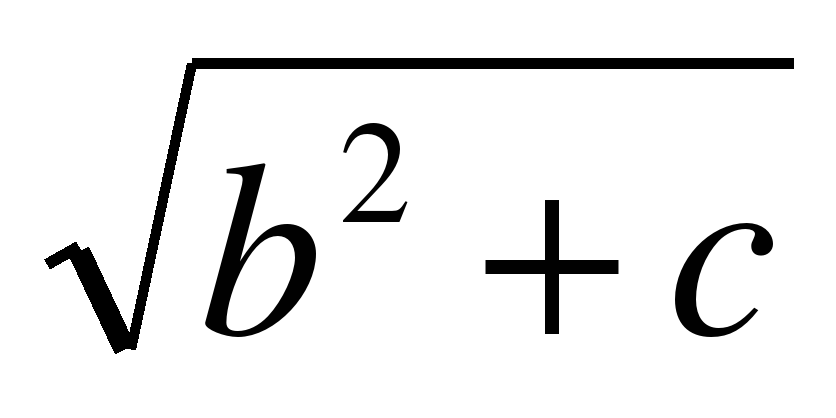
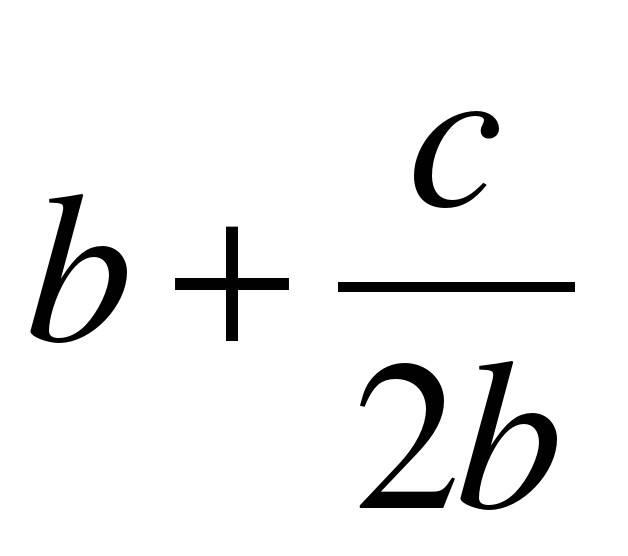
Например, если a = 112, то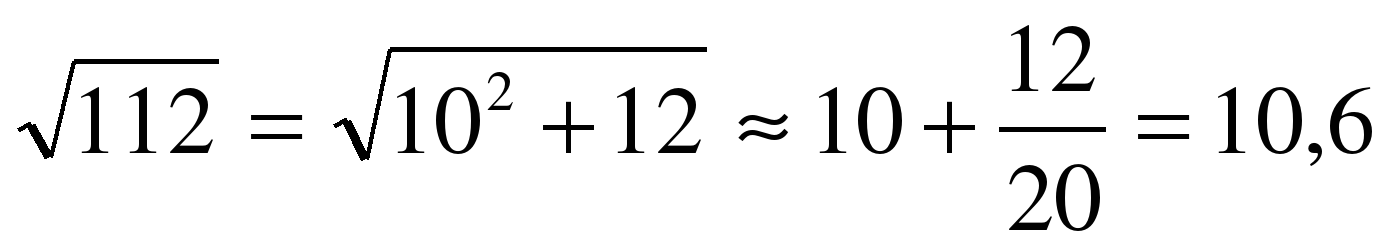 
. Проверка показывает, что 10,62 = 112,36.
Указанный метод извлечения квадратного корня подробно описан древнегреческим ученым Героном Александрийским (I в. н.э.).
В эпоху Возрождения европейские математики обозначали корень латинским словом Radix (корень), а затем сокращенно буквой R (отсюда произошел термин «радикал», которым принято называть знак корня). Некоторые немецкие математики XV в. для обозначения квадратного корня пользовались точкой. Эту точку ставили перед числом, из которого нужно извлечь корень. Позднее вместо точки стали ставить ромбик 
, впоследствии знак 
и над выражением, из которого извлекается корень, проводили черту. Затем знак и черту стали соединять. Такие записи встречаются в «Геометрии» Декарта и «Всеобщей арифметике» Ньютона. Современная запись корня появилась в книге «Руководство алгебры» французского математика М.Ролля (1652 – 1719).
9 класс
Об уравнениях высших степеней.
Неполные квадратные уравнения и частные случаи полных квадратных уравнений умели решать еще вавилоняне (2 тыс. лет до н.э.). Отдельные виды квадратных уравнений решали древнегреческие математики, сводя их решение к геометрическим построениям.
Примеры решения уравнений 3-й степени не были известны ни древнегреческой, ни арабской науке. В алгебраических трактатах арабских математиков IX – XV вв., кроме решения уравнений и систем уравнений 1-й и 2-й степеней, рассматриваются решения кубических уравнений частных видов. Однако способы решения этих уравнений приводили к нахождению приближенных значений корней.
Общее уравнение 3-й степени имеет вид ах3 + bx2 + сх + d = 0, где а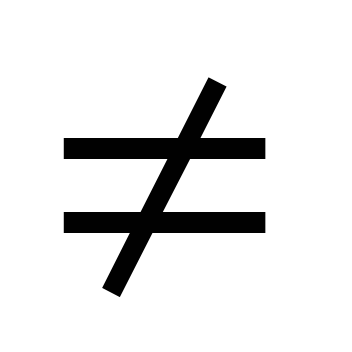 
0. Давно было известно, что с помощью введения новой переменной это уравнение можно свести к уравнению вида х3 + px + q = 0.
Впервые формулу для отыскания положительного корня уравнения
х3 + px = q, где p 0 и q 0, вывел итальянский математик Сципион Даль Ферро (1465 - 1526), но держал ее в тайне. Только в конце жизни он сообщил своему ученику Фиори об открытии. Одновременно вопросом об общем решении уравнений 3-й степени занимался другой итальянский математик – Н.Тарталья (ок. 1499 - 1557), который нашел способы решения уравнений х3 + px = q, х3 + q = px, х3 = px + q и частных случаев уравнения х3 + px2 = q (p и q - положительные числа). В 1535 г. Между Фиори и Тартальей состоялся научный поединок, на котором Тарталья одержал блестящую победу (он за 2 ч решил все 30 предложенных ему задач, в то время как Фиори не решил ни одной задачи Тартальи).
С 1539 г. решением кубических уравнений начинает заниматься итальянский математик Д.Кардано (1501 - 1576). Он узнал об открытии Тартальи, который не публиковал своих трудов. В 1545 г. вышла книга Кардано «Великое искусство, или О правилах алгебры», где наряду с другими вопросами алгебры рассматриваются общие способы решения кубических уравнений. В эту книгу Кардано включил также метод решения уравнений 4-й степени, открытый его учеником Л.Феррари (1522 - 1565).
Вопрос о том, кому принадлежит приоритет открытия формулы корней кубических уравнений – Тарталье или Кардано, не решен до сих пор.
В формуле корней квадратного уравнения используется знак корня – радикал. Через радикалы (корни 2, 3 и 4-й степеней) выражаются и корни уравнений
3-й и 4-й степеней.
После того как были найдены формулы решений уравнений 3-й и 4-й степеней, усилия многих математиков были направлены на то, чтобы отыскать формулы решений уравнений любых степеней. На решение этой проблемы ушло около 300 лет, и лишь в 20-х гг. XIX в. норвежский математик Н.Абель (1802 - 1829) доказал, что в общем случае корни уравнений 5–й и более высоких степеней не могут быть выражены через радикалы. Французский математик Э.Галуа (1811 - 1832) выделил класс алгебраических уравнений, которые разрешимы в радикалах.
Использование алгебраических уравнений позволило дать более тонкую классификацию действительных чисел.
7 класс
Как появилась алгебра.
Алгебра как искусство решать уравнения зародилась очень давно в связи с потребностями практики, в результате поиска общих приемов решения однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приемы решения линейных уравнений.
Слово «алгебра» возникло после появления трактата «Китай аль-джебр валь-мукабала» математика и астронома из г.Хивы Мухаммеда Бен Мусса аль-Хорезми (787 – ок.850). Термин «аль-джебр» , взятый из названия этой книги, в дальнейшем стал употребляться как «алгебра».
До XVI в. изложение алгебры велось в основном словесно. Буквенные обозначения и математические знаки появлялись постепенно. Знаки « + » и « - » впервые встречаются у немецких алгебраистов XVI в. Несколько позже вводится знак « 
» для умножения. Знак деления « : » был введен лишь в XVII в. Решительный шаг в использовании алгебраической символики был сделан в XVI в., когда французский математик Франсуа Виет (1540 - 1603) и его современники стали применять буквы для обозначения не только неизвестных (что делалось и ранее), но и любых чисел. Однако эта символика еще отличалась от современной. Так, Виет для обозначения неизвестного числа применял букву N (Numerus – число), для квадрата и куба неизвестного – буквы Q (Quadratus - квадрат) и C (Cubus – куб). Например, запись уравнения х3 – 8х2 + 16х = 40 у Виета выглядела бы так:
1C – 8Q + 16N aequ. 40 (aequali - равно).
В процессе развития алгебра из науки об уравнениях преобразовалась в науку об операциях, более или менее сходных с действиями над числами. Современная алгебра – один из основных разделов математики
Школьный курс алгебры включает, кроме некоторых алгебраических сведений, отдельные вопросы из других разделов математики (функции, метод координат, приближенные вычисления, теория вероятностей и др.).
