| Актуализация знаний | Учитель сообщает тему урока и ставит перед учащимися вопрос: «Исходя из темы, какую цель для достижения на уроке вы себе поставите?»
Учитель сообщает, что в 7 классе, работая с электронными таблицами, ребята строили различные диаграммы и графики, т.е. они уже умеют визуализировать данные. Т.о. осталось научиться средствам анализа.
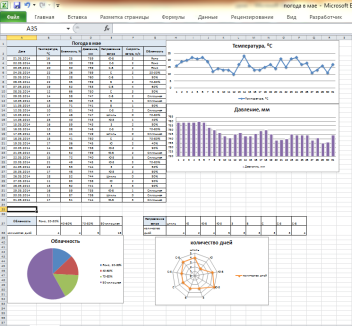
Предлагается посмотреть на работы, которые были сделаны учащимися в 7 классе.
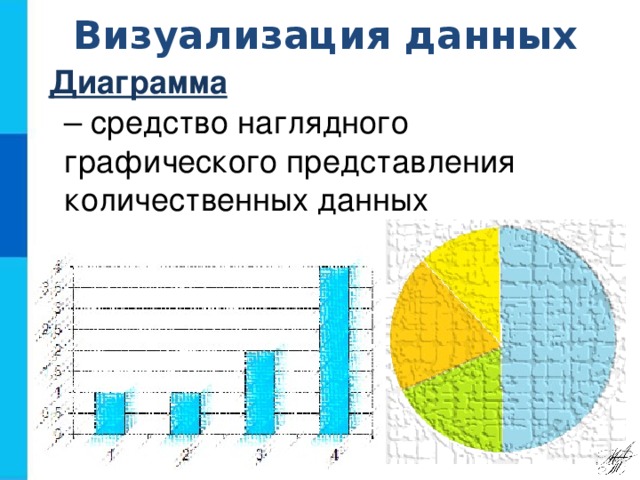
Пока открываются работы, учитель задает вопрос «А для чего нужны диаграммы? Учитель соглашается с тем, что диаграмма является средством наглядного графического представления количественных данных.
Какие типы диаграмм использовались для визуализации данных?
А в каких сферах деятельности человека могут использоваться диаграммы и графики?
| Учащиеся записывают тему.
Определяют цель урока: например, научиться анализировать и визуализировать данные с помощью диаграмм
Учащиеся открывают файл «Погода» из папки Практикум.
Для визуализации и наглядного представления данных
график, гистограмма или столбчатая диаграмма, круговая диаграмма и лепестковая или роза ветров
Отвечают на вопрос | 
(слайд 1)
(работа на компьютерах и на доске).
(слайд 2)
На доске чертит схему: 
|
| Изучение нового материала Формирование умения читать диаграммы | Учитель предлагает рассмотреть первый пример, для этого откройте лист уже имеющейся ЭТ, который называется ПРИМЕР 1
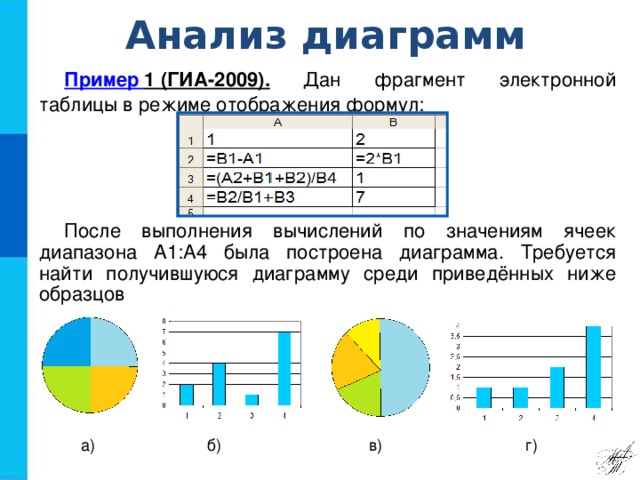
Читает задание «Дан фрагмент электронной таблицы в режиме отображения формул. После выполнения вычислений по значениям ячеек диапазона А1:А4 была построена диаграмма. Требуется найти получившуюся диаграмму среди приведённых ниже образцов. Для начала перейдем в режим отображения значений, для этого на ленте найдите вкладку Формулы, в разделе Зависимости формул нажмите кнопку Показать формулы. После вычислений по формулам в ячейках таблицы будут значения. (анимация по щелчку) По условию диаграмма построена по значениям ячеек диапазона А1:А4. Диапазон А1:А4 содержит три одинаковых значения - три единицы; четвёртое значение - это 3, что равно сумме трёх других значений. На диаграмме значениям диапазона А1:А4 должны соответствовать три равных по площади столбца или сектора, а также столбец или сектор, площадь которого равна сумме площадей трёх других столбцов или секторов. Таким условиям соответствует только диаграмма в).
Объясните, почему нам не подошли диаграммы под буквами а), б) и г)?
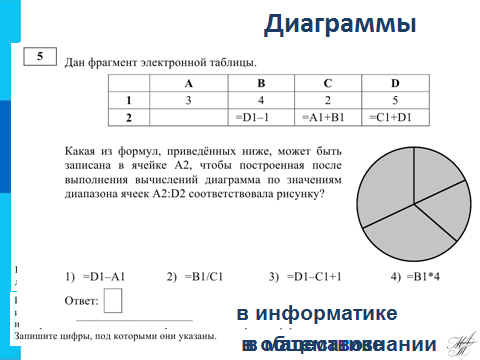
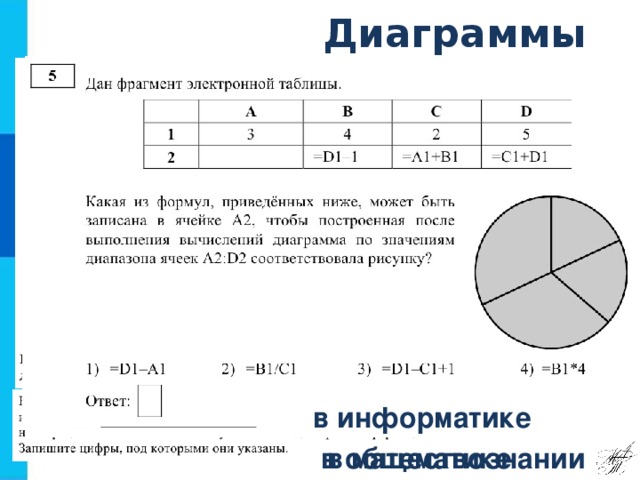
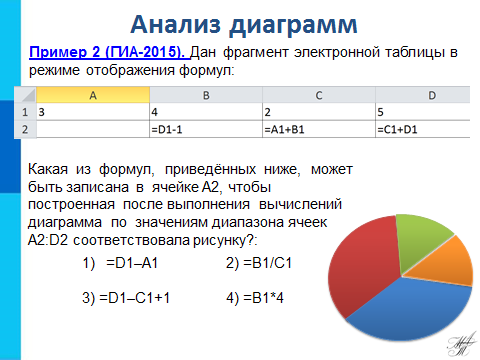
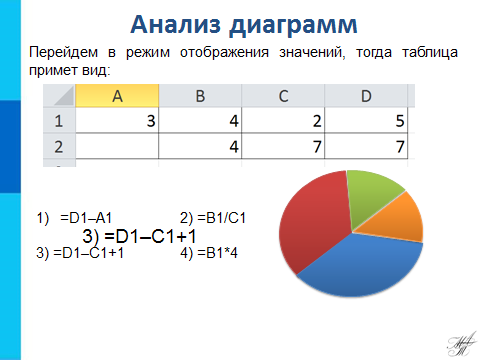
Теперь рассмотрим пример 2, где по диаграмме нужно подобрать формулу. Откройте лист ПРИМЕР 2. Дан фрагмент электронной таблицы в режиме отображения формул. Какая из формул, приведённых ниже, может быть записана в ячейке A2, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку? Перейдем в режим отображения значений, тогда в таблице появятся значения. Из рисунка видно, что сегменты диаграммы попарно равны, следовательно в таблице также должны быть две пары одинаковых чисел. Одна пара есть и раны они 7, следовательно, другая пара чисел равна 4, т.е. в ячейке А2 находится число 4, которое можно найти по какой формуле? (№3) (анимация по щелчку) Для проверки решения можно дописать эту формулу в ячейку А2, выделить диапазон A2:D2 и построить для него круговую диаграмму.
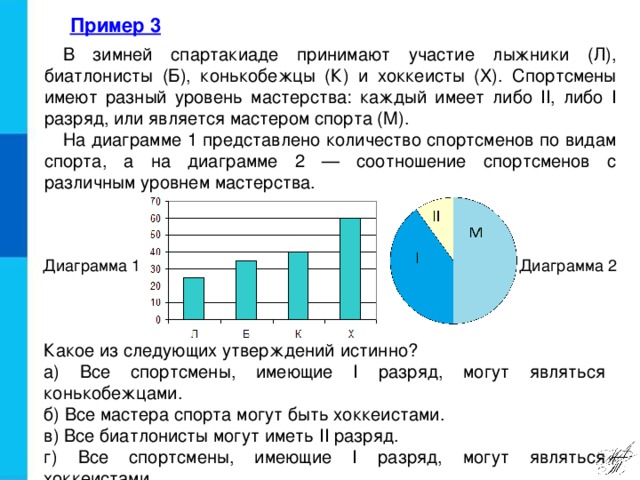
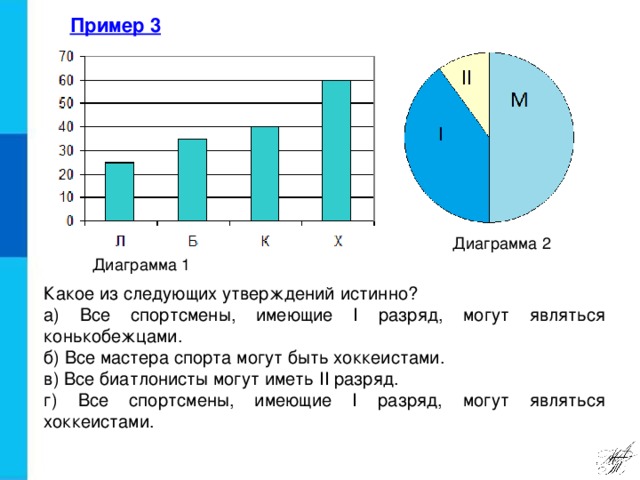
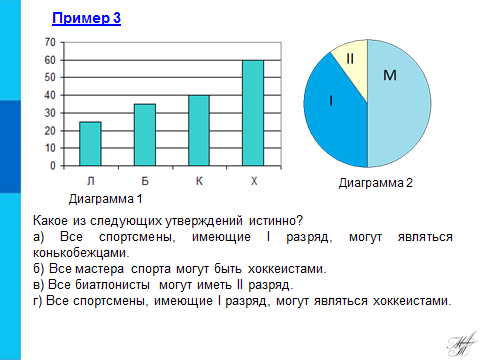
Рассмотрим пример 3, который в таком же виде встречается в ОГЭ по математике. В зимней спартакиаде принимают участие лыжники (Л), биатлонисты (Б), конькобежцы (К) и хоккеисты (X). Спортсмены имеют разный уровень мастерства: каждый имеет либо II, либо I разряд, или является мастером спорта (М). На диаграмме 1 представлено количество спортсменов по видам спорта, а на диаграмме 2 — соотношение спортсменов с различным уровнем мастерства. Какое из следующих утверждений истинно? а) Все спортсмены, имеющие I разряд, могут являться конькобежцами. б) Все мастера спорта могут быть хоккеистами. в) Все биатлонисты могут иметь II разряд. г) Все спортсмены, имеющие I разряд, могут являться хоккеистами.
С чего начать? Из столбчатой диаграммы мы можем найти общее количество спортсменов: 25+35+40+60=160 человек. Из круговой диаграммы видим, что половина их них т.е. 80– мастера спорта, что полностью отрицает пункт б). 1-й и 2-й разряды занимают вторую половину и из круговой диаграммы примерно видно отношение как 3:1. Т.е. 1-й разряд – ¾ спортсменов – 60 человек и пункт а) не подходит, а 2-й разряд – ¼ спортсменов, что составляет 20 человек и пункт в) также не подходит. Проверим пункт г) «Все спортсмены, имеющие I разряд 60 чел, могут являться хоккеистами – 60 чел» верно. | Учащиеся открывают пример 1 и читают задание.
Учащиеся переходят в режим отображения значений
Учащиеся рассуждают вместе с учителем и делают вывод о выборе верного варианта.
В а) все части равны, что не соответствует условию; в б) все столбцы разные, что не соответствует значениям таблицы; в г) равных по высоте только 2 столбца вместо 3
Учащиеся открывают пример 2 и читают задание.
Учащиеся переходят в режим отображения значений Учащиеся рассуждают вместе с учителем и делают вывод о выборе верного варианта.
Проверяют верность выбранной формулы, вводят ее в ячейку А2 и по полученным значениям строят круговую диаграмму. Сравнивают полученную диаграмму и исходную. | 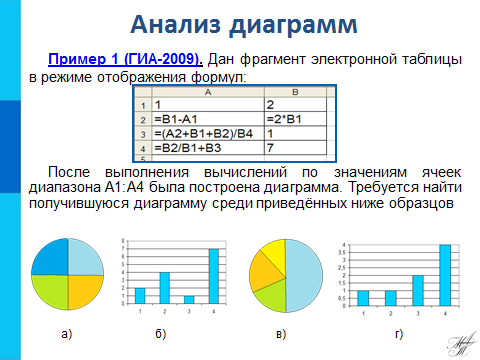
(слайд 4)

(слайд 5)
(слайд 6)
(слайд 7)

(слайд 8)
(слайд 9)
|