Алгебра высказываний. Основные операции алгебры высказываний

В ДАННОЙ ПРЕЗЕНТАЦИИ ПРЕДСТАВЛЕНА ТЕМА «АЛГЕБРА ВЫСКАЗЫВАНИЙ.ОСНОВНЫЕ ОПЕРАЦИИ».

ПРЕЗЕНТАЦИЯ ВКЛЮЧАЕТ СЛЕДУЮЩИЕ РАЗДЕЛЫ:

ПОНЯТИЕ ЛОГИКИ.
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ.
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.
ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЯ: ДИЗЬЮНКЦИЯ, КОНЬЮНКЦИЯ, МПЛИКАЦИЯ, ЭКВИВАЛЕНЦИЯ.
РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ.
ПРИМЕРЫ РЕШЕНИЯ ТАБЛИЦ ИСТЕННОСТИ.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Алгебра высказываний. Основные операции алгебры высказываний »

АЛГЕБРА ВЫСКАЗЫВАНИЙ. ОСНОВНЫЕ ОПЕРАЦИИ

Что такое логика?

LOGOS (ГРЕЧ.) – СЛОВО, ПОНЯТИЕ, РАССУЖДЕНИЕ, РАЗУМ

СЛОВО «ЛОГИКА» ОБОЗНАЧАЕТ СОВОКУПНОСТЬ ПРАВИЛ, КОТОРЫМ ПОДЧИНЯЕТСЯ ПРОЦЕСС МЫШЛЕНИЯ.

ОСНОВНЫМИ ФОРМАМИ АБСТРАКТНОГО МЫШЛЕНИЯ ЯВЛЯЮТСЯ: ПОНЯТИЯ, СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ .

ПОНЯТИЕ - ФОРМА МЫШЛЕНИЯ, В КОТОРОЙ

ОТРАЖАЮТСЯ СУЩЕСТВЕННЫЕ ПРИЗНАКИ

ОТДЕЛЬНОГО ПРЕДМЕТА ИЛИ КЛАССА

ОДНОРОДНЫХ ПРЕДМЕТОВ. (ТРАПЕЦИЯ, ДОМ)

СУЖДЕНИЕ - МЫСЛЬ, В КОТОРОЙ ЧТО-ЛИБО УТВЕРЖДАЕТСЯ ИЛИ ОТРИЦАЕТСЯ О ПРЕДМЕТАХ. (ВЕСНА НАСТУПИЛА, И ГРАЧИ ПРИЛЕТЕЛИ)

УМОЗАКЛЮЧЕНИЕ - ПРИЕМ МЫШЛЕНИЯ, ПОСРЕДСТВОМ КОТОРОГО ИЗ ИСХОДНОГО ЗНАНИЯ ПОЛУЧАЕТСЯ НОВОЕ ЗНАНИЕ.

(ВСЕ МЕТАЛЛЫ - ПРОСТЫЕ ВЕЩЕСТВА)

ЛОГИКА (ФОРМАЛЬНАЯ) - НАУКА О ЗАКОНАХ И ФОРМАХ ПРАВИЛЬНОГО МЫШЛЕНИЯ.

МАТЕМАТИЧЕСКАЯ ЛОГИКА - ИЗУЧАЕТ ЛОГИЧЕСКИЕ СВЯЗИ И ОТНОШЕНИЯ, ЛЕЖАЩИЕ В ОСНОВЕ ЛОГИЧЕСКОГО (ДЕДУКТИВНОГО) ВЫВОДА.

ЭТАПЫ РАЗВИТИЯ ЛОГИКИ

АРИСТОТЕЛЬ (384-322 гг. до н.э.) - ОСНОВОПОЛОЖНИК ЛОГИКИ

КНИГИ:

«КАТЕГОРИИ»
«ПЕРВАЯ АНАЛИТИКА»
«ВТОРАЯ АНАЛИТИКА»

( ИССЛЕДОВАЛ РАЗЛИЧНЫЕ ФОРМЫ РАССУЖДЕНИЙ , ВВЕЛ ПОНЯТИЕ СИЛЛОГИЗМА)

СИЛЛОГИЗМ - РАССУЖДЕНИЕ, В

КОТОРОМ ИЗ ЗАДАННЫХ ДВУХ

СУЖДЕНИЙ ВЫВОДИТСЯ ТРЕТЬЕ.

АРИСТОТЕЛЬ ВЫДЕЛИЛ ВСЕ ПРАВИЛЬНЫЕ

ФОРМЫ СИЛЛОГИЗМОВ, КОТОРЫЕ МОЖНО

СОСТАВИТЬ ИЗ РАССУЖДЕНИЙ ВИДА:

- «Все А суть В»

- «Некоторые А суть В»

- «Все А не суть В»

«Некоторые А не суть В»

Логика, основанная на теории

силлогизмов называется классической.

Декарт Рене (1596-1650, фр. философ, математик)

РЕКОМЕНДОВАЛ В ЛОГИКЕ ИСПОЛЬЗОВАТЬ МАТЕМАТИЧЕСКИЕ МЕТОДЫ.

Лейбниц Г.В . (1646-1716, нем. ученый и математик)

Предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной системы счисления.

Логика обретает символьный язык, конкретность законов, распространяется за рамки гуманитарных наук.

Джордж Буль (1815-1864, анл.) - основоположник мат. логики .

1847 г. – Джордж Буль в работе «Математический анализ логики» изложил основы булевой алгебры.

РАЗРАБОТАЛ АЛФАВИТ, ОРФОГРАФИЮ И ГРАММАТИКУ.

1815 – 1864 гг. благодаря трудам математика Дж. Буля появился раздел математической логики, получивший название алгебры логики или булевой алгебры .

ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Логика оказала влияние на развитие математики, прежде всего теории множеств, функциональных систем, алгоритмов, рекурсивных функций.

Логика оказала влияние на развитие математики, прежде всего теории множеств, функциональных систем, алгоритмов, рекурсивных функций.

2) Математическая логика является средством для изучения деятельности мозга - для решения этой самой важной проблемы биологии и науки вообще.

3) В гуманитарных науках

(логика, криминалистика).

4) Идеи и аппарат логики используется в кибернетике, ВТ и электротехнике (построены компьютеры на основе законов математической

логики).

1938 г. – американский математик и инженер Клод Шеннон связал Булеву алгебру (аппарат математической логики), двоичную систему кодирования и релейно-контактные переключательные схемы, заложив основы будущих ЭВМ.

5) Идеи и аппарат логики используется в программировании, базах данных и экспертных системах.

PROLOG – язык логического программирования

ОСНОВНЫЕ ОПЕРАЦИИ АЛГЕБРЫ ВЫСКАЗЫВАНИЙ

ДИЗЪЮНКЦИЯ (ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)

СОЕДИНЕНИЕ ДВУХ ВЫСКАЗЫВАНИЙ А И В В ОДНО С ПОМОЩЬЮ СОЮЗА «ИЛИ»,

УПОТРЕБЛЯЕМОГО В НЕИСКЛЮЧАЮЩЕМ ВИДЕ.

ОПРЕДЕЛЕНИЕ:

ДИЗЪЮНКЦИЯ ДВУХ ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ ЛОЖНА ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОБА ВЫСКАЗЫВАНИЯ ЛОЖНЫ.

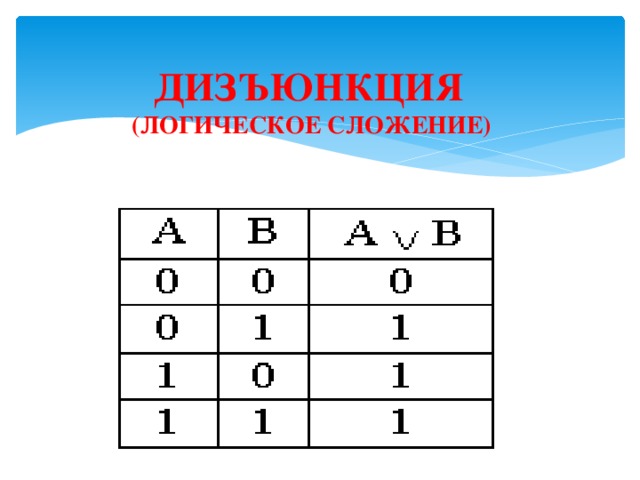
ДИЗЪЮНКЦИЯ

(ЛОГИЧЕСКОЕ СЛОЖЕНИЕ)

КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ) -

Определение:

КОНЪЮНКЦИЯ ДВУХ

ЛОГИЧЕСКИХ ВЫСКАЗЫВАНИЙ

ИСТИННА ТОГДА И ТОЛЬКО ТОГДА,

КОГДА ОБА ВЫСКАЗЫВАНИЯ

ИСТИННЫ.

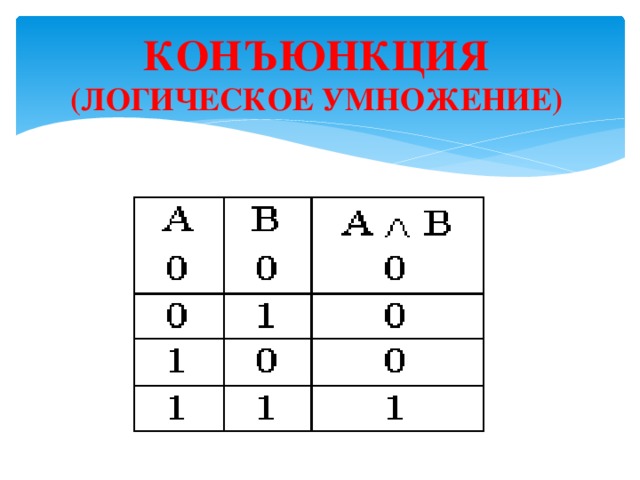
КОНЪЮНКЦИЯ (ЛОГИЧЕСКОЕ УМНОЖЕНИЕ)

ИМПЛИКАЦИЯ

ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ

«ЕСЛИ . . . , ТО . . .»

Определение:

ИМПЛИКАЦИЯ ВЫСКАЗЫВАНИЙ

ЛОЖНА ЛИШЬ В СЛУЧАЕ, КОГДА А

ИСТИННО, А В ЛОЖНО.

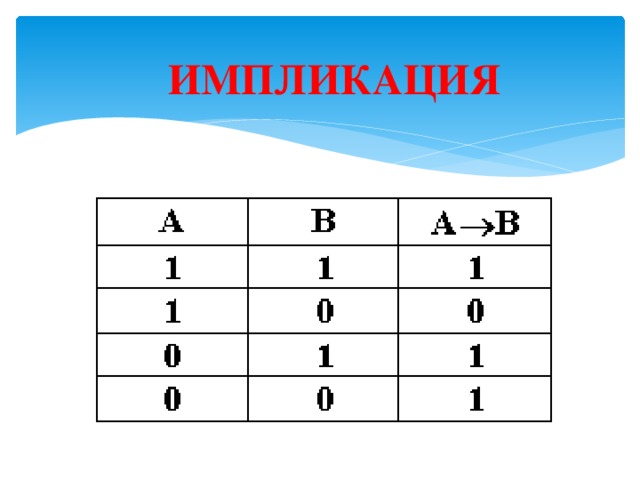
ИМПЛИКАЦИЯ

ЭКВИВАЛЕНЦИЯ

ЛОГИЧЕСКАЯ ОПЕРАЦИЯ, СООТВЕТСТВУЮЩАЯ СОЮЗУ «ТОГДА И ТОЛЬКО ТОГДА, КОГДА …»

Определение:

ЭКВИВАЛЕНЦИЯ ДВУХ

ВЫСКАЗЫВАНИЙ ИСТИННА В ТОМ И ТОЛЬКО ТОМ СЛУЧАЕ, КОГДА ОБА ЭТИ

ВЫСКАЗЫВАНИЯ ИСТИННЫ ИЛИ ЛОЖНЫ.

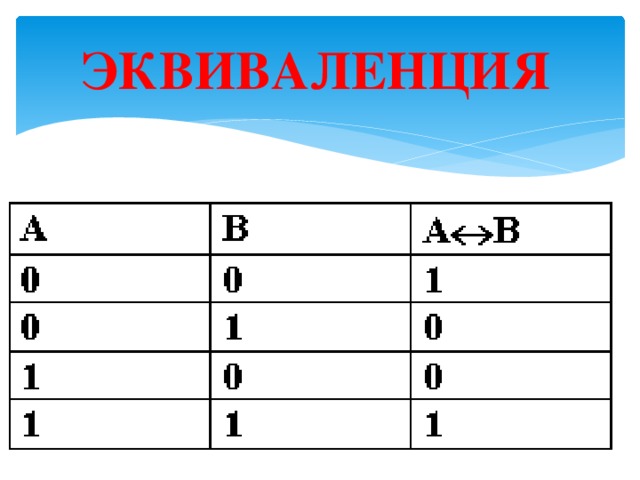
ЭКВИВАЛЕНЦИЯ

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ:

ИНВЕРСИЯ;
КОНЪЮНКЦИЯ;
ДИЗЪЮНКЦИЯ;
ИМПЛИКАЦИЯ И ЭКВИВАЛЕНТНОСТЬ .

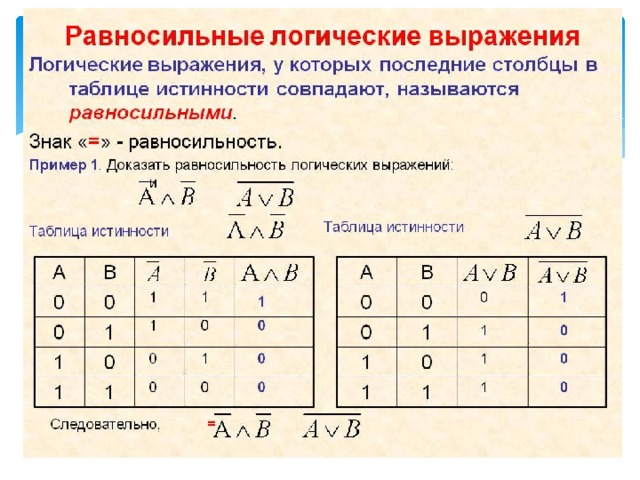
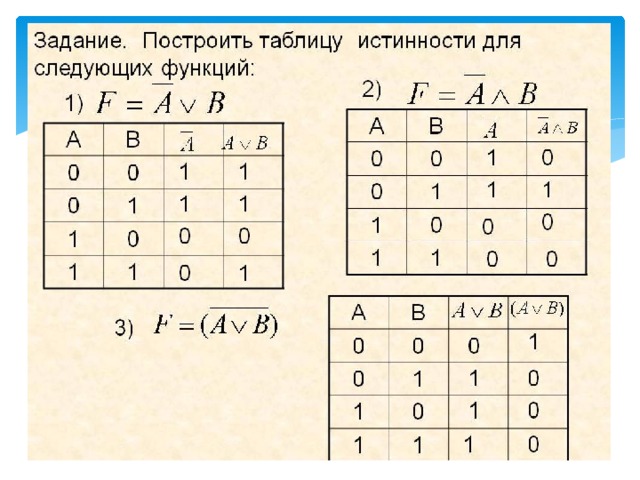
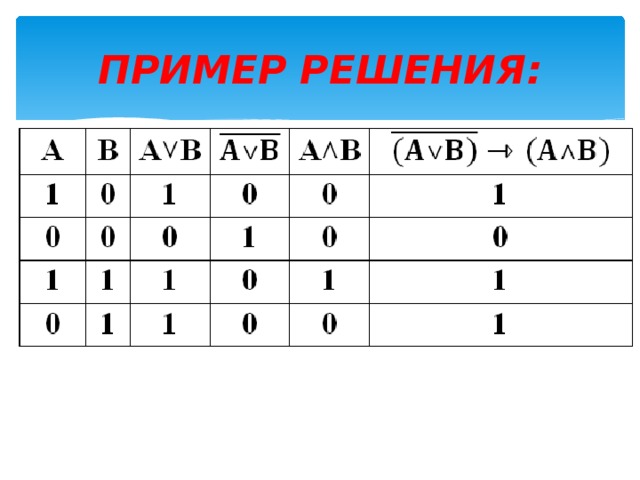
ПРИМЕР РЕШЕНИЯ:

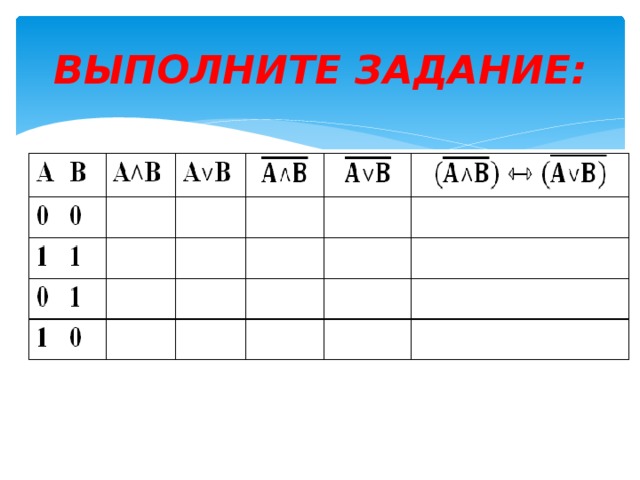
ВЫПОЛНИТЕ ЗАДАНИЕ:

ТАБЛИЦА №1:

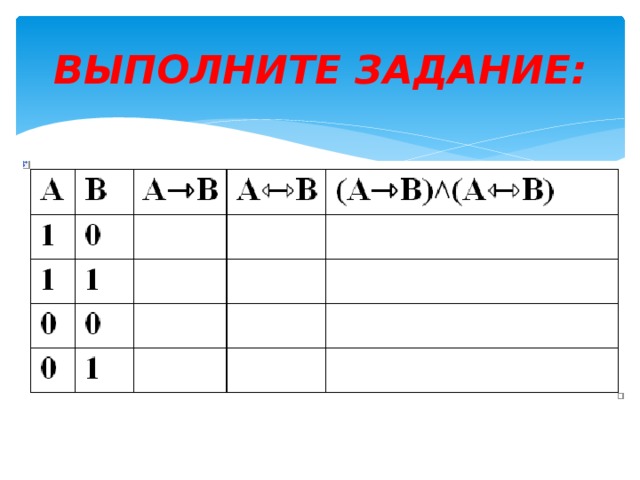
ВЫПОЛНИТЕ ЗАДАНИЕ:

ТАБЛИЦА № 2

ВЫПОЛНИТЕ ЗАДАНИЕ:

ТАБЛИЦА № 3

ВЫПОЛНИТЕ ЗАДАНИЕ:

СОСТАВЬТЕ ВЫРАЖЕНИЕ В 7 ДЕЙСТВИЙ С ИСПОЛЬЗОВАНИЕМ ИЗВЕСТНЫХ ВАМ ЛОГИЧЕСКИХ ОПЕРАЦИЙ И ЗАПИШИТЕ ДЛЯ НЕЕ ТАБЛИЦУ ИСТЕННОСТИ.

Предмет: Информатика

Категория: Презентации

Целевая аудитория: 9 класс

Скачать
Алгебра высказываний. Основные операции алгебры высказываний

Автор: Надейкин Владислав Анатольевич

Дата: 25.11.2014

Номер свидетельства: 135679

Похожие файлы

Методическая разработка урока по ФГОС "Истинность высказываний. Логические операции" 8 класс

object(ArrayObject)#865 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(170) "Методическая разработка урока по ФГОС "Истинность высказываний. Логические операции" 8 класс"
    ["seo_title"] => string(98) "mietodichieskaia_razrabotka_uroka_po_fgos_istinnost_vyskazyvanii_loghichieskiie_opieratsii_8_klass"
    ["file_id"] => string(6) "349894"
    ["category_seo"] => string(11) "informatika"
    ["subcategory_seo"] => string(12) "planirovanie"
    ["date"] => string(10) "1476702745"
  }
}

Основные понятия алгебры логики. Логические выражения и логические операции.

object(ArrayObject)#887 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(142) "Основные понятия алгебры логики. Логические выражения и логические операции."
    ["seo_title"] => string(85) "osnovnyieponiatiiaalghiebryloghikiloghichieskiievyrazhieniiailoghichieskiieopieratsii"
    ["file_id"] => string(6) "311040"
    ["category_seo"] => string(11) "informatika"
    ["subcategory_seo"] => string(11) "presentacii"
    ["date"] => string(10) "1459148826"
  }
}

Элементы алгебры логики

object(ArrayObject)#865 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(44) "Элементы алгебры логики"
    ["seo_title"] => string(23) "elementy_algebry_logiki"
    ["file_id"] => string(6) "484633"
    ["category_seo"] => string(11) "informatika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1541784193"
  }
}

Логические операции.

object(ArrayObject)#887 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(38) "Логические операции."
    ["seo_title"] => string(25) "loghichieskiie-opieratsii"
    ["file_id"] => string(6) "299250"
    ["category_seo"] => string(11) "informatika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1456487124"
  }
}

Методическая разработка по теме "Алгебра логики" для студентов 1 курса по дисциплине "Информатика и ИКТ"

object(ArrayObject)#865 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(190) "Методическая разработка по теме "Алгебра логики" для студентов 1 курса по дисциплине "Информатика и ИКТ" "
    ["seo_title"] => string(113) "mietodichieskaia-razrabotka-po-tiemie-alghiebra-loghiki-dlia-studientov-1-kursa-po-distsiplinie-informatika-i-ikt"
    ["file_id"] => string(6) "139121"
    ["category_seo"] => string(11) "informatika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1417653108"
  }
}

Алгебра высказываний. Основные операции алгебры высказываний

Просмотр содержимого документа «Алгебра высказываний. Основные операции алгебры высказываний »

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Алгебра высказываний. Основные операции алгебры высказываний »