Урок -исследование "Сумма углов треугольника", геометрия 7 класс

Геометрия 7 класс

Учитель математики МОУ СОШ№

г.о.Стрежевой Томской области

Кошелева Вера Валерьевна

УМК Л.С.Атанасян «Геометрия 7-9»

Тема: Сумма углов треугольника.

Цели урока: создать условия для самостоятельного формулирования и доказательства теоремы о сумме углов треугольника; организовать деятельность обучающихся по восприятию, осмыслению и первичному закреплению новых знаний и способов деятельности.

Задачи урока: - формировать умения самостоятельно формулировать задание:

и определять его цель, планировать алгоритм его выполнения,

корректировать работу по ходу ее выполнения;

формировать умения участвовать в диалоге; слушать и понимать других,

высказывать свою точку зрения и аргументировано ее отстаивать с

помощью фактов и дополнительных сведений, принимать участие в

работе парами, договариваться и приходить к общему решению.

Сценарий урока.

1. Организационный момент.

Вступительное слово. - Ни на миг не прерывается живая связь между поколениями, ежедневно мы усваиваем опыт, накопленный нашими предками. Древние греки, на основе наблюдений и из практического опыта, делали выводы, высказывали предположения-гипотезы, а затем на встречах ученых - симпозиумах, эти гипотезы пытались обосновать и доказать. В то время и сложилось утверждение: «В споре рождается истина». Наш сегодняшний урок тоже будет похож на небольшой симпозиум. Мы выскажем своё предположение по вопросу, попытаемся его доказать, и если у нас это получится, то посмотрим, как его можно будет применять при решении задач. А эпиграфом нашего урока, я хочу предложить слова Пифагора:

1. Актуализация опорных знаний.

Вопрос учителя: Прежде чем приступить к работе, вспомним, что изучает наука «Геометрия»?

Ответ учеников: Геометрия – это наука об измерении земли, о свойствах геометрических фигур

Вопрос учителя: Изучению какой фигуры мы уделяем больше всего внимания в 7 классе?

Ответ учеников: Треугольнику.

Вопрос учителя: Как вы думаете, почему именно с треугольника мы начинаем изучать геометрию?

Ответ учеников: Треугольник самая простая геометрическая фигура,

Учитель: Действительно, треугольник самая простая, но при этом самая жёсткая фигура, и

свойства её человек узнал ещё в глубокой древности. Эта фигура имеет широкое

практическое применение в практической жизни при строительстве домов, мостов и

других сооружений. Хоть треугольник и самый простой по виду многоугольник,

но по количеству свойств он опережает многие другие фигуры.

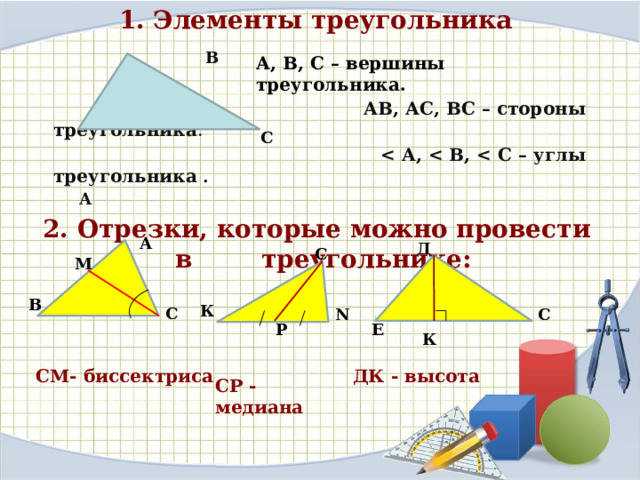
Давайте вспомним: 1) элементы треугольника (вершины, стороны, углы)

2) отрезки, которые можно провести в треугольнике

(биссектрисы, медианы, высоты).

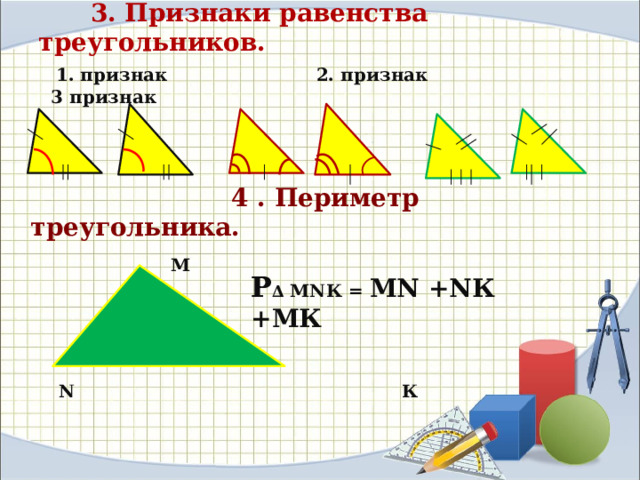
3) признаки равенства треугольников

4) что называется периметром треугольника?

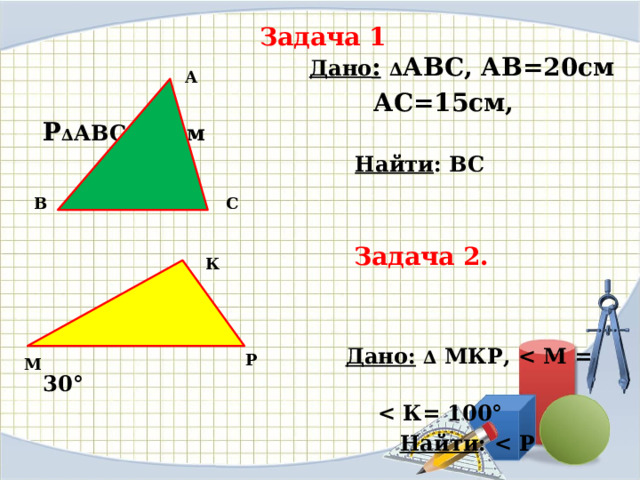
Задача1.

В Дано: АВС, Р = 60см

АС = 15см, АВ = 20см

Найти: ВС

А С

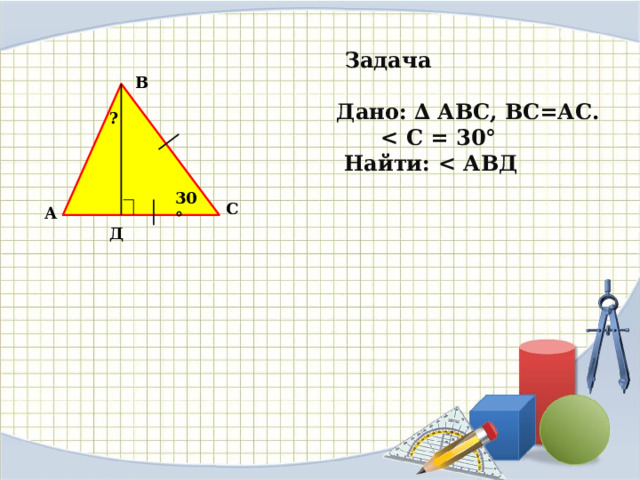
Задача2.

В Дано: АВС,

=

Найти: С

А С

Вопрос учителя: Сможем ли мы решить вторую задачу?

Ответ учеников: Нет.

Вопрос учителя: Что нам необходимо знать для того, чтобы решить эту задачу?

Ответ учеников: Для нахождения третьего угла, если по аналогии с задачей 1, нам необходимо знать

сумму углов треугольника.

Учитель: Тогда попробуйте сами сформулировать тему урока и запишите её в тетрадь,

а также проговорите цель урока.

Ученики: Записывают тему урока в тетрадь и озвучивают цель урока.

Учитель: Но для успешной работы на уроке нам необходимо вспомнить

с

1

Задание 3. (устно по слайду) Ответьте на вопросы:

1. К

   а

   2

   ак называется прямая, которая пересекает две другие?

2. С

   в

   4

   3

   5

   6

   7

   8

   колько неразвёрнутых углов образуется при пересечении двух прямых секущей?

3. Какие пары углов образуются?

4. Учитель: Я показываю пары углов, а вы даёте им название.

Задание 4 (устно по слайду)

Закончите предложение:

1. Две прямые называются параллельными, если …………………………….

2. Если две параллельные прямые пересечены секущей, то накрест лежащие углы ……….

3. Если две стороны угла образуют прямую, то этот угол называется ………

4. Градусная мера развёрнутого угла равна ………………………………

Учитель: Ну что ж, теоретически вы подкованы неплохо. Я думаю, что успех нам обеспечен.

1. Открытие новых знаний.

Учитель: Сейчас я хочу предложить вам выступить в роли исследователей и сделать математическое обоснование своих наблюдений и предположений. Каждый из вас побывает в роли первооткрывателя, если будет внимательным и наблюдательным.

Я предлагаю классу разделиться на три группы (по рядам). Четвёртая группа будет состоять из двух учащихся (самых мудрых): Алексея Федотова и Ромы Морозевича.

Задание трём группам одно: путём исследования выдвинуть гипотезу о сумме углов треугольника. Задание четвёртой группе: путём решения задач выдвинуть гипотезу о сумме углов треугольника.

Задание 1 группе: Ребятам выдаются различные бумажные модели треугольников. Путём перегибания получить прямоугольник так, чтобы вершины всех углов треугольника находились в одной точке, и сделать вывод о сумме углов треугольника.

Задание 2 группе: На парте три треугольника разных видов: остроугольный, прямоугольный, тупоугольный. Отрежьте углы этих треугольников и попытайтесь найти их сумму, сложив их вместе так, чтобы вершины всех углов треугольника находились в одной точке. Сделайте вывод о сумме углов треугольника.

Задание 3 группе: На карточках построены различные по виду треугольники. Измерьте углы каждого треугольника с помощью транспортира. Данные измерений занесите в таблицу. Найдите сумму углов каждого треугольника. И сделайте вывод.

Задание 4 группе (А.Федотов и Р.Морозевич) : По готовым чертежам найти все углы треугольника, а затем найти их сумму. Сделать вывод о сумме углов треугольника.

(По окончании работы каждая группа представляет свои результаты)

Учитель: Посмотрите результаты ваших исследований. У первой группы получилось, что углы в сумме дают 180⁰, у второй группы тоже получилось, что в сумме дают 180⁰, у третьей группы не всё так гладко, как у предыдущих двух (наверное транспортир подвёл или первые две не совсем правы). У Лёши с Ромой тоже получилось в сумме 180⁰, но у них даны были некоторые углы.

Вопрос учителя: Можем ли мы утверждать, что сумма углов любого треугольника равна 180⁰? Или это было случайным совпадением?

Ответ учеников: Да, можем.

Учитель: Действительно, очень часто учёные сначала экспериментальным путём устанавливают некоторые факты, а потом обосновывают их при помощи логических рассуждений. Это очень часто происходит в химии, физике, биологии, геометрии. Давайте и мы попытаемся доказать вывод, который получили в результате исследований.

Задание. (работа в парах)

На каждой парте имеются листы с готовыми чертежами. Запишите условие теоремы и попытайтесь устно доказать теорему о сумме углов треугольника.

(Роман и Алексей у доски)

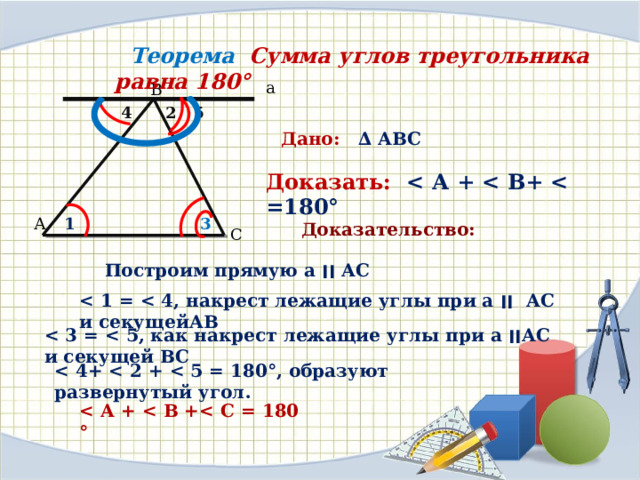
ТЕОРЕМА: Сумма углов треугольника равна 180⁰.

М

К

4

5

ДОКАЗАТЕЛЬСТВО:

1) проведём через вершину В прямую MN параллельную стороне ….......

2) угол 1 = углу 4, ( ………. ……………………углы при пересечении параллельных прямых…… и …. секущей ……)

3) угол 3 = углу 5 ( ………. …………….углы при пересечении параллельных прямых…… и ….. секущей …..)

4) угол 4 + угол 2 + угол 5 =………, так как образуют …………………. угол

5) из (2),(3), (4) получаем угол 1 + угол 2 + угол 3 = =………..

ТЕОРЕМА ДОКАЗАНА.

(Формулировку и доказательство проговорить и продемонстрировать на слайде)

1. Закрепление нового материала. (первичная проверка понимания изученного материала)

Учитель: Итак, теорема доказана. Значит ею можно пользоваться при решении задач.

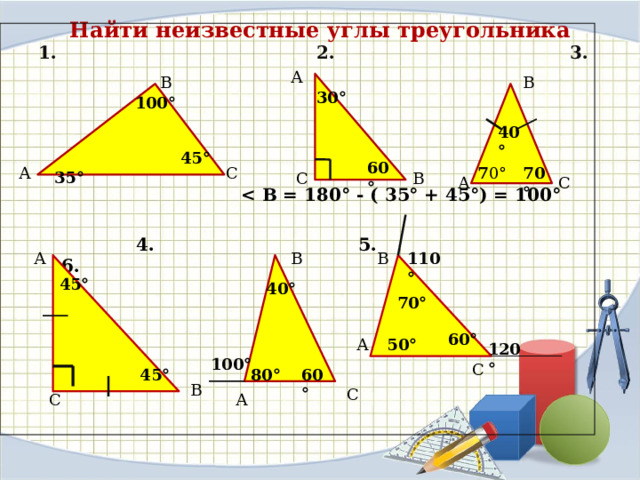
Решим несложные задачи по готовым чертежам (чертежи и задачи на слайде)

Вопрос учителя: Ребята, как вы считаете, существует ли треугольник с углами 90⁰, 5⁰, 95⁰?

Ответ учеников: Нет, т.к сумма углов больше 180⁰.

Вопрос учителя: Существует ли треугольник с углами 110⁰, 3⁰, 85⁰?

Ответ учеников: Нет, т.к сумма углов больше 180⁰.

Учитель: Ещё великий математик В.Ф.Коган сказал «Легче остановить Солнце, легче сдвинуть Землю, чем изменить сумму углов треугольника»

Вопрос учителя: Тогда у меня возникают вопросы: Сколько прямых углов может быть в треугольнике? Сколько тупых углов может быть в треугольнике?

Ответ учеников: В треугольнике может быть только один прямой угол, а остальные острые, или один тупой угол, а остальные острые.

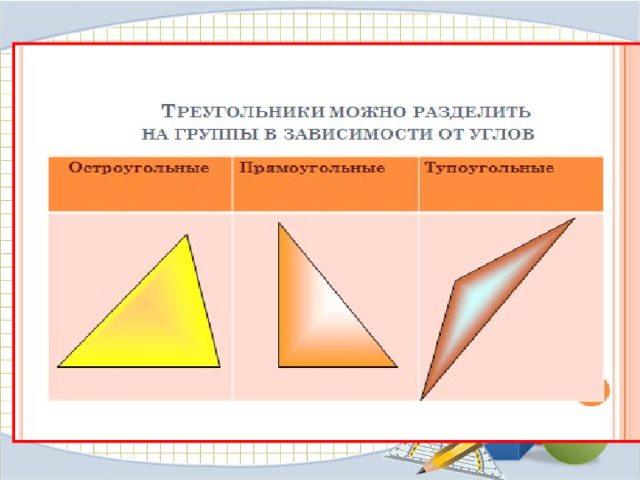
Вопрос учителя: Раз это так, то на какие группы можно разделить все треугольники по виду углов?

Ответ учеников: Прямоугольные, тупоугольные, остроугольные.

Учитель: Каждый у себя в тетради начертите и подпишите прямоугольный треугольник, тупоугольный и остроугольный треугольники. Выделите основные углы, благодаря которым треугольник получил определённое название (ребята чертят и подписывают) .

Задание по карточкам (индивидуально с самопроверкой)

(проверить с помощью слайда)

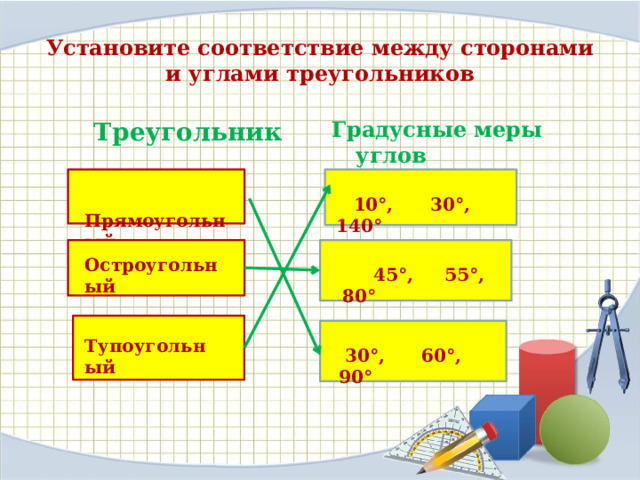
Установите соответствие между градусными мерами углов и названиями треугольников

10⁰ 30⁰ 140⁰

прямоугольный

45⁰ 55⁰ 80⁰

80000008080140⁰

Тупоугольный

30⁰ 60⁰ 90⁰

остроугольный

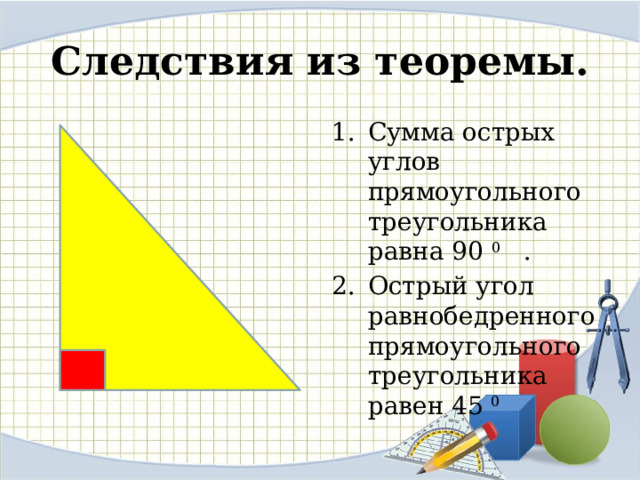
Учитель: Мы с Вами знаем, что из некоторых теорем в геометрии существуют полезные следствия, которые с успехом применяются при решении задач. Из открытой и доказанной нами теоремы существует одно полезное очень следствие, касающееся прямоугольного треугольника.

Именно прямоугольному треугольнику больше всего внимания уделяется в задачах ОГЭ и ЕГЭ.

Попробуйте это следствие сформулировать сами. На каждой парте лежит таблица вопросов. Дайте ответ на каждый вопрос и сделайте вывод.

З адание (работа в парах).

Вопрос	Ответ
Сколько прямых углов в прямоугольном треугольнике?
Какими по виду будут остальные два угла?
Чему равна сумма всех углов в прямоугольном треугольнике?
Сколько градусов в сумме дадут острые углы прямоугольного треугольника?
Какова градусная мера острого угла равнобедренного треугольника?

Затем выслушать выводы нескольких пар и следствие из теоремы записать в тетрадь.

Следствия из теоремы о сумме углов треугольника:

1. Сумма двух острых углов прямоугольного треугольника равна 90⁰.

2. Острый угол равнобедренного прямоугольного треугольника равен 45⁰.

1. Тест –достижения (с взаимопроверкой)

(проверить с помощью слайда)

Учитель: Время нашего урока подходит к концу. И мне хотелось бы посмотреть насколько прочно вы усвоили ещё одно из свойств самой простой, но самой жёсткой фигуры в геометрии , треугольника.

Фамилия ____________________ Вариант 1. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 400 и 600? …………… Два угла треугольника равны 1000 и 500. Найдите третий угол. ………… Два угла треугольника равны по 300 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при вершине равен 400. Чему равны углы при основании?..................

Фамилия ____________________ Вариант 2. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 1300 и 700? …………… Два угла треугольника равны 400 и 600. Найдите третий угол. ………… Два угла треугольника равны по 600 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при основании равен 700. Чему равен угол при вершине?..................

1. Рефлексия. (подведение итогов урока)

Притча: Шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил тяжелые камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»

Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.

• Кто возил камни? (поднимите жёлтые треугольники)

• Кто выполнял свою работу? (поднимите оранжевые треугольники)

• Кто строил храм? (поднимите розовые треугольники)

1. Домашнее задание.

1. Выучить теорему о сумме углов треугольника п.30-31.

2. Найти другие доказательства этой теоремы в интернете (по желанию)

3. №223(а,б), №225

СПАСИБО ЗА УРОК!

Задание 1 группе

Путём перегибания получить прямоугольник так, чтобы вершины всех углов треугольника находились в одной точке, и сделать вывод о сумме углов треугольника.

…………………………………………………………………………………

Задание 2 группе:

На парте три треугольника разных видов:

остроугольный, прямоугольный, тупоугольный. Отрежьте углы этих треугольников и попытайтесь найти их сумму, сложив их вместе так, чтобы вершины всех углов треугольника находились в одной точке. Сделайте вывод о сумме углов треугольника.

……………………………………………………………………………………………………………………..

Задание 3 группе:

На карточках построены различные по виду треугольники. Измерьте углы каждого треугольника с помощью транспортира. Данные измерений занесите в таблицу. Найдите сумму углов каждого треугольника. И сделайте вывод.

углы				сумма
Розовый треугольник
Оранжевый треугольник
Зелёный треугольник

Задание для ученика №1

Дано: АВС,

В

а а || АС

1

2

, ,

Найти:

А

С

Задание для ученика №2

Дано: АВС,

В

а || АВ

, ,

Найти:

А

1

С

2

ОПОРНАЯ СХЕМА

ТЕОРЕМА: Сумма углов треугольника равна 180⁰.

ДОКАЗАТЕЛЬСТВО:

1) проведём через вершину В прямую MN параллельную стороне ….......

2) угол 1 = углу 4, ( ………. ……………………углы при пересечении параллельных прямых…… и …. секущей ……)

3) угол 3 = углу 5 ( ………. …………….углы при пересечении параллельных прямых…… и ….. секущей …..)

4) угол 4 + угол 2 + угол 5 =………, так как образуют …………………. угол

5) из (2),(3), (4) получаем угол 1 + угол 2 + угол 3 = =………..

ТЕОРЕМА ДОКАЗАНА.

ОПОРНАЯ СХЕМА

ТЕОРЕМА: Сумма углов треугольника равна 180⁰.

ДОКАЗАТЕЛЬСТВО:

1) проведём через вершину В прямую MN параллельную стороне ….......

2) угол 1 = углу 4, ( ………. ……………………углы при пересечении параллельных прямых…… и …. секущей ……)

3) угол 3 = углу 5 ( ………. …………….углы при пересечении параллельных прямых…… и ….. секущей …..)

4) угол 4 + угол 2 + угол 5 =………, так как образуют …………………. угол

5) из (2),(3), (4) получаем угол 1 + угол 2 + угол 3 = =………..

ТЕОРЕМА ДОКАЗАНА.

З адание (работа в парах).

Вопрос	Ответ
Сколько прямых углов в прямоугольном треугольнике?
Какими по виду будут остальные два угла?
Чему равна сумма всех углов в прямоугольном треугольнике?
Сколько градусов в сумме дадут острые углы прямоугольного треугольника?
Какова градусная мера острого угла равнобедренного треугольника?

… ……………………………………………………………………………………………………………………………………………Задание (работа в парах).

Вопрос	Ответ
Сколько прямых углов в прямоугольном треугольнике?
Какими по виду будут остальные два угла?
Чему равна сумма всех углов в прямоугольном треугольнике?
Сколько градусов в сумме дадут острые углы прямоугольного треугольника?
Какова градусная мера острого угла равнобедренного треугольника?

Установите соответствие между градусными мерами углов и названиями треугольников

10⁰ 30⁰ 140⁰

прямоугольный

45⁰ 55⁰ 80⁰

80000008080140⁰

Тупоугольный

30⁰ 60⁰ 90⁰

остроугольный

…………………………………………………………………………………………………..

Установите соответствие между градусными мерами углов и названиями треугольников

10⁰ 30⁰ 140⁰

прямоугольный

45⁰ 55⁰ 80⁰

80000008080140⁰

Тупоугольный

30⁰ 60⁰ 90⁰

остроугольный

………………………………………………………………………………………………………..

Установите соответствие между градусными мерами углов и названиями треугольников

10⁰ 30⁰ 140⁰

прямоугольный

45⁰ 55⁰ 80⁰

80000008080140⁰

Тупоугольный

30⁰ 60⁰ 90⁰

остроугольный

Фамилия ____________________ Вариант 1. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 400 и 600? …………… Два угла треугольника равны 1000 и 500. Найдите третий угол. ………… Два угла треугольника равны по 300 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при вершине равен 400. Чему равны углы при основании?..................	Фамилия ____________________ Вариант 2. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 1300 и 700? …………… Два угла треугольника равны 400 и 600. Найдите третий угол. ………… Два угла треугольника равны по 600 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при основании равен 700. Чему равен угол при вершине?..................
Фамилия ____________________ Вариант 1. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 400 и 600? …………… Два угла треугольника равны 1000 и 500. Найдите третий угол. ………… Два угла треугольника равны по 300 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при вершине равен 400. Чему равны углы при основании?..................	Фамилия ____________________ Вариант 2. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 1300 и 700? …………… Два угла треугольника равны 400 и 600. Найдите третий угол. ………… Два угла треугольника равны по 600 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при основании равен 700. Чему равен угол при вершине?..................
Фамилия ____________________ Вариант 1. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 400 и 600? …………… Два угла треугольника равны 1000 и 500. Найдите третий угол. ………… Два угла треугольника равны по 300 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при вершине равен 400. Чему равны углы при основании?..................	Фамилия ____________________ Вариант 2. Закончите предложение: Сумма углов треугольника равна ……. Существует ли треугольник, два угла которого равны 1300 и 700? …………… Два угла треугольника равны 400 и 600. Найдите третий угол. ………… Два угла треугольника равны по 600 каждый. Чему равен третий угол? …………….. В равнобедренном треугольнике угол при основании равен 700. Чему равен угол при вершине?..................

«Сумма углов треугольника» 7 класс.

… Да, путь познания не гладок. Но знаем мы со школьных лет, Загадок больше, чем разгадок, И поиска предела нет. Пифагор .

В жизни треугольники встречаются повсюду: при строительстве домов, мостов и других сооружений

1. Элементы треугольника

В

АВ, АС, ВС – стороны треугольника .

.

В

А

2. Отрезки, которые можно провести в треугольнике:

А, В, С – вершины треугольника.

С

А

Д

С

М

С

К

С

N

Р

Е

К

СМ- биссектриса

ДК - высота

СР - медиана

4 . Периметр треугольника.

М

N К

3. Признаки равенства треугольников. 1. признак 2. признак 3 признак

Р ∆ МNК = МN +NК +МК

Задача 1

Дано : ∆ АВС, АВ=20см

АС=15см, Р ∆ АВС=60см

Найти : ВС

Задача 2.

Дано: ∆ МКР,

Найти :

А

В

С

К

Р

М

2

1

3

8

Назовите углы, образованные при пересечении двух прямых третьей прямой.

1и

соответственные углы

накрест лежащие углы

односторонние углы

7

4

5

6

Закончите предложение:

1. Две прямые называются параллельными,

если……………………………………..

2. Если две параллельные прямые пересечены

секущей, то накрестлежащие углы………

3. Если две стороны угла образуют прямую,

то он называется ………………..

4. Градусная мера развёрнутого угла равна …

1

3

В

С

Теорема Сумма углов треугольника равна 180°

а

4 2 5

Дано: ∆ АВС

Доказать:

А

Доказательство:

Построим прямую а ׀׀ АС

׀׀ АС и секущейАВ

׀׀ АС и секущей ВС

Найти неизвестные углы треугольника 1. 2. 3.

60°

4. 5. 6.

А

В

В

30°

100°

40°

45°

35°

60°

7 0°

70°

А

С

С

В

С

А

В

А

В

110°

70°

45°

40°

А

50°

120°

100°

С

45°

60°

80°

В

С

А

С

Дайте ответ:

• Существует ли треугольник с углами

90 0 , 5 0 , 95 0 ?

2. Существует ли треугольник с углами

110 0 , 3 0 , 85 0 ?

• В.Ф. Коган сказал: « Легче остановить Солнце. Легче сдвинуть Землю, чем изменить сумму углов треугольника».
• Свойство суммы углов треугольника было открыто эмпирически, т. е. опытным путем еще в Древнем Египте. Однако дошедшие до нас сведения относятся к более позднему времени. Древнегреческий ученый Прокл (410-585г.г. н.э.) утверждал, комментируя книгу « Начала» Евклида, что согласно Евдему Родосскому (сумма углов треугольника равна развер-
• нутому углу.)

•  

Установите соответствие между сторонами и углами треугольников

Треугольник

Градусные меры углов

Прямоугольный

10°, 30°, 140°

Остроугольный

45°, 55°, 80°

Тупоугольный

30°, 60°, 90°

Следствия из теоремы.

• Сумма острых углов прямоугольного треугольника равна 90 0 .
• Острый угол равнобедренного прямоугольного треугольника равен 45 0

Тест – достижения.

Вариант 1.

Вариант 2.

• 180 0
• Да
• 30 0
• 120 0

• 180 0
• Нет
• 80 0
• 60 0

5 . 70 0

5 . 40 0

Домашнее задание: 1. п.30- 31. (выучить теорему и её следствия) № 223 ( б, г ), № 324. 2. Найти по интернету другие доказательства теоремы о сумме углов треугольника. (по желанию) 3. №223(а,б), 225

Спасибо за урок!

Задача Дано: ∆ АВС, ВС=АС. Найти:

В

?

30°

С

А

Д