Тема: Среднии линии треугольника и трапеции/1/.
Цели урока:
Образовательные: ввести определение средней линии треугольника; изучить свойства средней линии треугольника;формировать умения и навыков применять знания о средней линии треугольника при решении задач. Изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять теорему в нестандартных ситуациях при решении задач. Формировать умение учащихся анализировать, обобщать, использовать элементы исследования, сравнения.
Развивающие: развивать геометрическое мышление учащихся при решении геометрических задач, интерес к предмету, познавательную и творческую деятельность учащихся, математическую речь, память, внимание; учить учащихся учиться математике, самостоятельно добывать знания. Развивать логическое мышление, воспитывать культуру математической речи.
Воспитательные: воспитывать у учащихся ответственное отношение к учебному труду, волю; формировать эмоциональную культуру и культуру общения.
Ход урок:
1. Организационный момент
2. Мотивация урока.
Девиз урока: «С любовью к ее величеству - науке геометрии».
3. Проверка домашнего задания:
а). №152,153,157,166.
б). -Какую теорему изучили на прошлом уроке?
-Сформулируйте ее.
-Как разделить отрезок на несколько равных частей?
Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать!
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И “по краю” и “внутри”
Тест “Истинно” или “ложно”
-Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны. (И)
-Высота равнобедренного треугольника является медианой, биссектрисой. (Л) (Пропущены слова: проведенная к основанию)
-Если три стороны треугольника равны трем сторонам другого треугольника, то такие треугольники равны. (Л) (Пропущено слово: соответственно)
-Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны. (И)
-В треугольнике углы при основании равны. (Л) (Пропущено слово: равностороннем или равнобедренном)
-Медиана равнобедренного треугольника, проведенная к основанию, называется высотой и биссектрисой. (И)
4. Изучение нового материала.
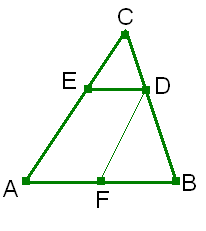
а).Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Практическое задание:1 ряд строит треугольник прямоугольный, 2 ряд – тупоугольный, 3 ряд – остроугольный. Далее:
-Постройте в треугольнике одну из средних линий. Обозначьте ее.
-Как расположена средняя линия относительно третьей стороны?
-Дети отвечают не очень утвердительно: я думаю, они параллельны; мне кажется, они параллельны; они параллельны; у меня они не параллельны.
-Измерьте третью сторону и среднюю линию треугольника. Что вы можете сказать по этому поводу?
-Дети высказывают свое мнение: у меня получилось, что средняя линия треугольника в два раза меньше третьей стороны; а у меня третья сторона почти в два раза больше средней линии.
Теорема. Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине.
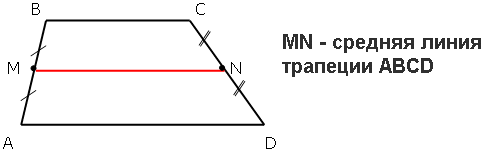
б).Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
-Верно ли определение: отрезок, соединяющий середины двух сторон трапеции, является средней линией? (Нет, отсутствует слово боковых сторон).
- А сколько средних линий можно построить в трапеции? (Только одну).
- Каким свойством обладает средняя линия трапеции? Измерьте основания трапеции и длину средней линии. Чему равна средняя линия? (Половине суммы оснований).
5. Закрепление нового материала: №140,143,162,164.
6.Домашнее задание:№141,144,163.
7. Итоги урока.
(10 см)
6.Домашнее задание: №165,166,167.
7.Итоги урока.
ont-family:"Times New Roman"'>