Признаки равенства треугольников

Действия учителя

Действия ученика

Записи на доске и в тетрадях

Начнем наш урок с выполнения устных заданий.

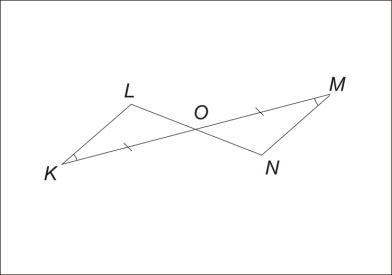
Задание 1. На рисунке изображены два треугольника. Докажите, что а) ∠L=∠N, б) KL=MN.

Что нам известно в задаче?

Нам известно, что KO=OM,

∠K=∠M

Дано:

∆KLO, ∆MNO,

KO=OM,

∠K=∠M

Что требуется доказать?

Нужно доказать, что ∠L=∠N, KL=MN.

Доказать:

а) ∠L=∠N,

б) KL=MN

Есть ли на рисунке равные треугольники, и если да, то какие и почему?

∆KLO=∆MNO по второму признаку, т. к. KO=MO, ∠K=∠M (по условию), ∠LOK=∠NOM как вертикальные.

Решение:

1. ∆KLO=∆MNO по второму признаку, т. к. KO=MO, ∠K=∠M (по условию), ∠LOK=∠NOM как вертикальные.

Какой вывод тогда можно сделать об углах ∠L и ∠N и отрезках KL и MN?

В равных треугольниках соответствующие элементы равны. Следовательно, ∠L=∠N, KL=MN.

2. В равных треугольниках соответствующие элементы равны. Следовательно, ∠L=∠N, KL=MN.

Как мы доказывали равенство двух отрезков или двух углов?

Мы рассматривали их как соответственные части двух равных треугольников.

Задание 2. Назовите биссектрису, медиану и высоту треугольника ABC.

CL – биссектриса, AM – медиана, BH – высота.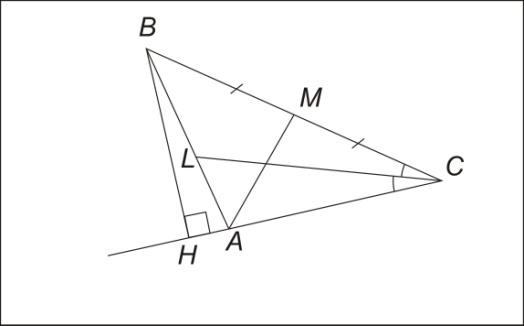

Назовите определение биссектрисы треугольника.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Что называется медианой треугольника?

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Что такое высота треугольника?

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Действия учителя

Действия ученика

Записи на доске и в тетрадях

Вы изучили большую и важную тему «Признаки равенства треугольников», изучили много теоретического материала. Научились решать разные виды задач на основе изученной теории. На следующем уроке вы пишите контрольную работу.

Поэтому сегодня вам следует обобщить и систематизировать полученные знания.

Это и будет нашей учебной задачей урока.

-

-

Действия учителя

Действия ученика

Записи на доске и в тетрадях

Для того чтобы обобщить и систематизировать полученные знания, давайте заполним специальную схему. (Учитель раздает канву-таблицу)

-

Систематизирующая таблица «Равенство треугольников»

Вспомните, с чего мы начинали изучение этой темы?

Изучение этой темы мы начали с рассмотрения понятия треугольника.

Изобразите произвольный треугольник ABC в рамке под словом «Треугольник».

Заполнение таблицы.

Что нужно сделать, чтобы изобразить треугольник?

Нужно отметить три точки, не лежащие на одной прямой, и соединить их отрезками.

Из каких элементов состоит треугольник?

Выпишите их в столбик в рамке «Элементы треугольника».

Треугольник состоит из вершин, сторон, углов.

Заполнение таблицы.

Давайте выпишем элементы треугольника ABC. Назовите вершины, стороны и углы ∆ABC.

Вершины: A, B, C.

Стороны: AB, BC, AC.

Углы: ∠A, ∠B, ∠C.

Заполнение таблицы.

Давайте проведем стрелку от рамки с понятием треугольника к рамке с элементами треугольника.

Стрелка в нашей таблице будет обозначать связь между понятиями и теоремами изученной темы.

Заполнение таблицы.

Что называется периметром треугольника?

Периметром треугольника называется сумма длин трех сторон этого треугольника.

Напишем в рамке «Периметр треугольника», чему равен периметр ∆ABC.

P_∆ABC = AB+BC+AC

Заполнение таблицы.

Давайте обозначим связь понятий треугольника и периметра треугольника стрелкой.

Заполнение таблицы.

Какие особые виды треугольников вы изучили?

Равнобедренные и равносторонние.

Проведите две стрелки от рамки «Треугольник» к соответствующим рамкам и подпишите их, как показано на слайде.

Заполнение таблицы.

Какой треугольник называется равнобедренным?

Треугольник называется равнобедренным, если две его стороны равны.

Обозначьте равные элементы равнобедренного треугольника.

AB=BC

Заполнение таблицы.

Какой треугольник называется равносторонним?

Треугольник называется равносторонним, если все его стороны равны.

Обозначьте равные элементы равностороннего треугольника.

AB=BC=AC

Заполнение таблицы.

Как связаны между собой равносторонний и равнобедренный треугольники?

Отметим эту связь стрелкой.

Любой равносторонний треугольник является равнобедренным.

Заполнение таблицы.

Какие свойства равнобедренного треугольника вы изучили?

Давайте заполним соответствующую рамку.

Обозначьте стрелкой связь понятия равнобедренного треугольника и свойств равнобедренного треугольника.

Свойства равнобедренного треугольника:

1) Углы при основании равны.

 2) Биссектриса, медиана и высота, проведенные к основанию, совпадают между собой.

Заполнение таблицы.

Пусть нам даны два треугольника. Какое действие мы можем выполнить с ними?

Мы можем сравнивать их на предмет равенства.

Давайте пропишем это в таблице. Обозначьте связь понятия треугольника и равенства треугольников.

Заполнение таблицы.

Сформулируйте определение равных треугольников.

Два треугольника называются равными, если их можно совместить наложением.

Схематически обозначим совмещение равных треугольников.

Заполнение таблицы.

Какими свойствами обладают равные треугольники?

Заполните соответствующую рамку.

Обозначьте стрелкой связь понятия равных треугольников и свойств равных треугольников.

Свойства равных треугольников:

 1) В равных треугольниках ∠A=∠A₁, ∠B=∠B₁, ∠C=∠C₁, AB=A₁B₁, BC=B₁C₁, AC=A₁C₁.

 2) В равных треугольниках против равных сторон лежат равные углы и против равных углов лежат равные стороны.

Заполнение таблицы.

С помощью чего вы умеете доказывать равенство треугольников?

По определению и, используя признаки равенства треугольников.

Проведите стрелку от понятия равенства треугольников к признакам равенства треугольников.

Заполнение таблицы.

Какие элементы треугольника должны быть равны по первому признаку равенства треугольников?

Отметим их в таблице и на рисунке.

Две стороны и угол между ними.

Заполнение таблицы.

Как мы доказывали первый признак равенства треугольников?

Зафиксируем это в таблице.

Мы накладывали один треугольник на другой.

Заполнение таблицы.

Какие элементы треугольника должны быть равны по второму признаку равенства треугольников?

Отметим их в таблице и на рисунке.

Сторона и два прилежащих к ней угла.

Заполнение таблицы.

Как мы доказывали второй признак равенства треугольников?

Зафиксируем это в таблице.

Мы накладывали один треугольник на другой.

Заполнение таблицы.

Какие элементы треугольника должны быть равны по третьему признаку равенства треугольников?

Отметим их в таблице и на рисунке.

Три стороны.

Заполнение таблицы.

Как мы доказывали второй признак равенства треугольников?

Зафиксируем это в таблице.

Мы прикладывали один треугольник к другому.

Заполнение таблицы.

Какие случаи расположения луча C₁C относительно угла A₁C₁B₁.

получаются при приложении двух треугольников?

Зафиксируем это в таблице.

Возможные случаи:

1) луч C₁C проходит внутри угла A₁C₁B₁;

2) луч C₁C совпадает с одной из сторон угла A₁C₁B₁;

3) луч C₁C проходит вне угла A₁C₁B₁.

Заполнение таблицы.

Что мы использовали при доказательстве равенства треугольников в каждом случае?

Мы использовали первый признак равенства треугольников и свойства равнобедренного треугольника.

Заполнение таблицы.

Отметим эти связи стрелками.

Заполнение таблицы.

Итак, мы с вами заполнили систематизирующую таблицу по теме «Равенство треугольников», в которой отразили изученные понятия и теоремы, а также связи между ними.

Действия учителя

Действия ученика

Записи на доске и в тетрадях

Чтобы закрепить наши умения применять изученный материал на практике, давайте решим следующую задачу.

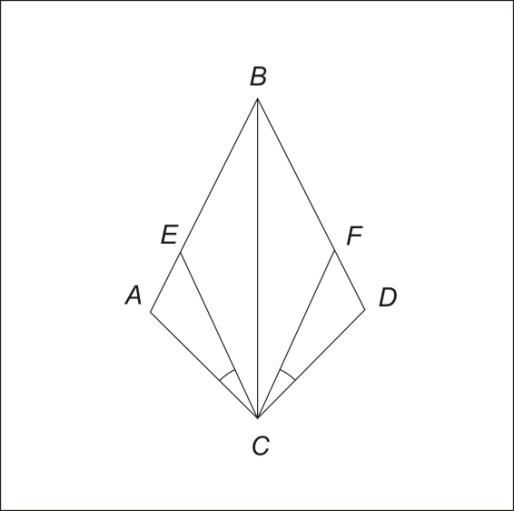
Задача

На рисунке AB=BD, ∠ACE=∠DCF, BC – биссектриса ∠ABD.

а) Докажите, что ∆AEC=∆DFC.

б) Докажите, что AE=FD.

в) Найдите ∠AEC, если известно, что ∠DFC=47˚.

Сделайте чертеж в тетради и давайте оформим условия.

Что нам дано по условию?

AB=BD, ∠ACE=∠DCF, BC – биссектриса ∠ABD

Дано: AB=BD, ∠ACE=∠DCF, BC – биссектриса ∠ABD, ∠DFC=47˚

Что требуется сделать в задаче?

а) Доказать, что ∆AEC=∆DFC.

б) Доказать, что AC=CD.

в) Найти ∠AEC.

а) Доказать, что ∆AEC=∆DFC.

б) Доказать, что AE=DF.

в) Найти ∠AEC.

Давайте решим задачу под пунктом а). Что требуется доказать?

∆AEC=∆DFC

Что нам известно об этих треугольниках?

∠ACE=∠DCF по условию.

Равенство каких пар элементов нужно знать еще, чтобы доказать равенство треугольников?

Нужно знать равенство пар двух прилежащих к известным углам сторон, чтобы доказать равенство треугольников по первому признаку, или знать равенство пары прилежащих сторон к известным углам и пару других углов, прилежащих к этой стороне, чтобы использовать второй признак равенства треугольников.

Каким образом мы можем доказать равенство недостающих элементов?

Рассмотрев их как соответствующие элементы равных треугольников.

Равенство каких треугольников, содержащих нужные элементы, мы можем доказать?

∆ABC и ∆DBC

Что нам известно об этих треугольниках?

AB=BD, BC – общая сторона, ∠ABC=∠DBC, т. к. BC – биссектриса ∠ABD.

Что тогда можно сказать о равенстве треугольников ∆ABC и ∆DBC?

∆ABC=∆DBC по первому признаку.

Зачем мы доказывали равенство этих треугольников?

Чтобы используя равенство соответствующих элементов, доказать равенство ∆AEC=∆DFC.

Равенство каких элементов мы можем использовать?

AC=CD, ∠BAC=∠BDC

Тогда что можно сказать о треугольниках ∆AEC и ∆DFC?

∆AEC=∆DFC по второму признаку, т. к. AC=CD, ∠BAC=∠BDC, ∠ACE=∠DCF.

Давайте оформим решение для пункта а).

Решение:

а) 1. ∆ABC=∆DBC по первому признаку, т. к. ∠ABC=∠DBC (BC – биссектриса ∠ABD), AB=BD (по условию), BC – общая сторона.

2. В равных треугольниках соответствующие элементы равны. Следовательно, AC=CD, ∠BAC=∠BDC.

3. ∆AEC=∆DFC по второму признаку, т. к. AC=CD, ∠BAC=∠BDC, ∠ACE=∠DCF.

Давайте решим задачу под пунктом б). Что требуется сделать?

Доказать, что AE=DF.

Что нужно сделать, что доказать равенство двух отрезков?

Нужно рассмотреть их как соответствующие элементы равных треугольников.

Соответствующими элементами каких треугольников являются эти отрезки?

∆AEC и ∆DFC

Что мы знаем об этих треугольниках?

∆AEC=∆DFC

Тогда какой вывод можно сделать об AE и DF?

В равных треугольниках соответствующие элементы равны, следовательно, AE=DF.

Оформим решение задачи под пунктом б).

б) ∆AEC=∆DFC согласно решению а). В равных треугольниках соответствующие элементы равны, следовательно, AE=DF.

Давайте решим задачу под пунктом в). Что требуется сделать?

Найти ∠AEC.

Как мы с вами искали величину угла?

Мы находили угол, величина которого известна, и доказывали равенство двух этих углов как соответственных в равных треугольниках.

Величина какого угла нам известна?

∠DFC=47˚.

Есть ли такие треугольники, в которых бы ∠AEC и ∠DFC были соответственными?

∆AEC и ∆DFC

Что мы знаем об этих треугольниках?

∆AEC=∆DFC

Тогда какой вывод можно сделать о величине ∠AEC?

В равных треугольниках соответствующие элементы равны. Следовательно, ∠AEC=∠DFC=47˚.

Оформим решение задачи под пунктом в).

в) ∆AEC=∆DFC согласно решению а). В равных треугольниках соответствующие элементы равны. Следовательно, ∠AEC=∠DFC=47˚.

Ответ: ∠AEC =47˚.

Действия учителя

Действия ученика

Записи на доске и в тетрадях

Какова была цель урока?

Цель урока - обобщить и систематизировать знания по теме «Признаки равенства треугольников».

Достигли мы её?

Да.

Как мы её достигли? (Возможные дополнительные вопросы: Какие понятия мы повторили? При помощи чего мы обобщали и систематизировали полученные знания? Какие виды задач мы повторили?)

Мы повторили понятия треугольника, равных и не равных треугольников, а так же теоремы: свойства равных треугольников, признаки равенства треугольников. С помощью заполнения таблицы мы обобщили и систематизировали полученные по этой теме знания. Мы повторили основные виды задач, для решения которых используются свойства равных треугольников, признаки равенства треугольников.

Домашнее задание:

№ 93, 94, 140, 162(а)