Конспект урока "Сумма углов треугольника"

Конспект урока открытия новых знаний с использованием ИКТ- технологий, критического мышления, практической работы для "открытия новых знаний"

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Конспект урока "Сумма углов треугольника"»

Треугольники. Сумма углов треугольника

Тип урока: изучение нового материала с использованием элементов исследования (урок-исследование).

Цели урока:

-обучающие -выявить практическим (исследовательским) путем значение суммы углов треугольника, сформулировать и доказать теорему о сумме углов треугольника и научить учащихся применять данную теорему к решению простейших задач;

-развивающие: развивать умения анализировать, сравнивать, обобщать, делать выводы, развивать внимание;

- воспитательные: развивать познавательный интерес через игровые моменты взаимоконтроля, взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, положительного эффекта настойчивости для достижения цели.

Методы: по источникам знаний: словесные, наглядные

По степени взаимодействия учитель-ученик: эвристическая беседа; Относительно дидактических задач: подготовка к восприятию; Относительно характера познавательной деятельности: репродуктивный, частично-поисковый Оборудование: Учебник, карточки.

Ход урока

К ,Р

ОРг. Момент

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей

«…Геометрия является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать».

Галилео Галилей (1564-1642 г.г., итальянский физик, астроном, философ, математик).

Актуализация и фиксирование индивидуального затруднения в пробном учебном действии

Анализ выполнения работы на сайте РЕШУ ОГЭ с последующей коррекцией ошибок , с ребятами допустившими ошибки.

Карточки (для детей выполнивших д. з без ошибок)

Д В Е

Д ано: Δ АВС, ДЕ АС

Найти: ÐА+ÐВ+ÐС.

А С

Мотивация и целеполагание

Ребята, посмотрите за кроссенс . найдите взаимосвязь между картинками и сформулируйте тему урока

-Как вы думаете, чему равна сумма углов треугольника?

-Это только гипотеза, которое требует доказательства.

-Сформулируем цели нашего урока.

Первичное изучение нового материала

Практическая работа

На каждой парте у учащихся лежит конверт с бумажными моделями треугольников разного цвета:

Один треугольник зеленого цвета, один треугольник желтого цвета;

Три равных треугольника синего, голубого и белого цвета.

Учащимся предлагается последовательно выполнить три практических задания с помощью выданных моделей, и решить вспомогательную задачу, т.е. самостоятельно в парах провести некоторую исследовательскую деятельность. После чего, сделать промежуточные выводы или выдвинуть гипотезу.

Практическое задание №1 (слайд №5).

Измерьте углы в выданных треугольниках зеленого и желтого цвета, результаты измерений запишите в тетрадь и найдите сумму углов в каждом треугольнике. Сравнить полученные результаты. Почему некоторые суммы совпали, а некоторые – нет? От чего это зависит?

Практическое задание №2 (слайд №6).

В желтом треугольнике обозначьте углы через №1, №2, №3. Оторвите их и совместите вершины углов так, чтобы образовался развернутый угол.

Проделайте те же действия и с зеленым треугольником.

Результат можно сверить с чертежом на слайде №6 (после щелчка).

Практическое задание №3 (слайд №7).

Расположите три равных треугольника так, чтобы получились параллельные прямые и углы №1, №2, №3 составили развернутый угол.

Результат можно сверить с чертежом на слайде №7 (после щелчка).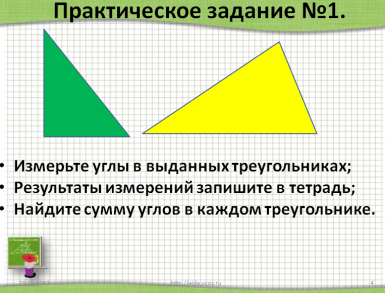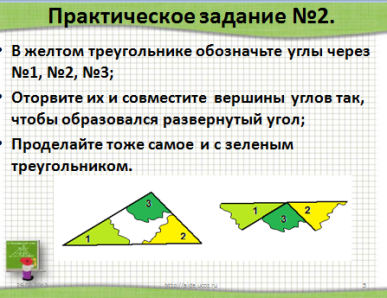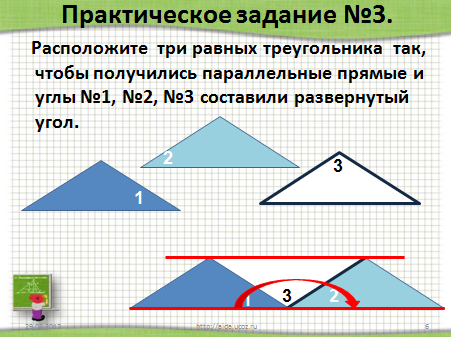

Слайд №5--Слайд №7.

Динамическая пауза

Динамическая пауза способствует снятию лишнего эмоционального напряжения, напряжения с глаз и смене позы учеников с сидячей на стоячую (разгрузка позвоночника). Учащиеся следят за перемещающейся фигурой, которая двигается по разным траекториям.

Сформулируем теорему, запишем в тетрадях: дано и что требуется доказать. Далее, учащимся предлагается обсудить метод доказательства, составить план доказательства и записать в тетрадях

Теорема. Сумма углов треугольника равна 180⁰.

Дано: Δ АВС.

Доказать:Ð1+Ð2+Ð3=180°.

План доказательства:

Доп. построение: прямая а ǁ АС;
Доказать равенство углов 1 и 4, 3 и 5;
Найти сумму углов 2,4,5;
Сделать вывод про сумму углов 1,2,3.

На слайде №10 последовательно выводится план доказательства (после щелчка). После этого, на экран щелчком выводится портрет Пифагора, как автора первого доказательства теоремы о сумме углов треугольника.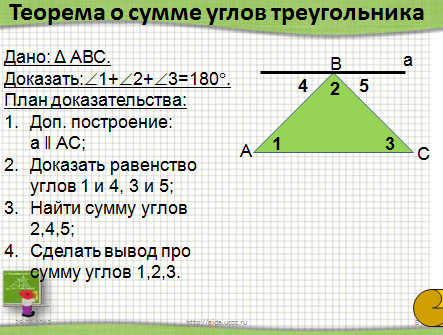

Первичное закрепление материала

На этом этапе урока проходит первичное закрепление изученного материала путем устного решения простейших задач по готовым чертежам. Но прежде, необходимо обратить внимание учащихся, для чего необходима новая теорема

(Чтобы находить угол треугольника, если известны два его угла или их сумма.)

Задание: Найти неизвестные углы в данных треугольниках на слайдах №12-13.

Вопрос учителя: Можно ли найти углы последнего треугольника? (Нет) При каких условиях можно находить углы треугольника? (Если известен вид треугольника, или градусная мера двух его углов).

Треугольники на слайде появляются по щелчку.

Если имеется запас времени, то учащимся можно предложить самостоятельно решить дополнительную задачу на слайде №14 с последующей общей проверкой.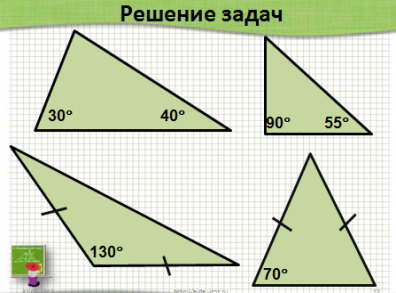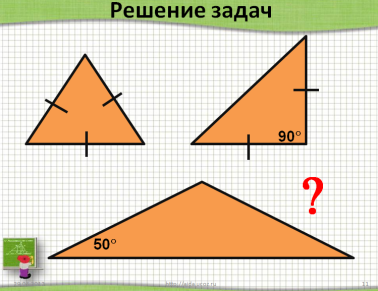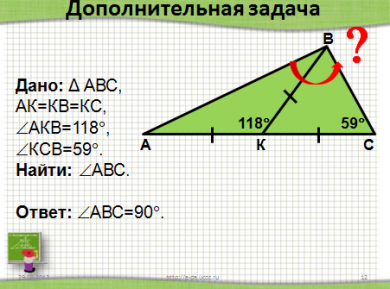

Слайд №12. Слайд №13. Слайд Первичная проверка усвоения материала

В качестве обратной связи проводиться первичная проверка знаний учащихся в формате мини-теста. Учащиеся самостоятельно выбирают в предложенных заданиях пронумерованные верные утверждения. В итоге должно получиться четырехзначное число, правильность которого проверяется тут же на слайде (после щелчка).

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Ответ:2231.

Слайд №15.

7. Рефлексия (слайд №15).

Итог. Д. з.

Доказательство теоремы. №254

самоопределение.

Проявляют интерес к креативной деятельности, активности при подготовке иллюстраций изучаемых понятий

Понимают смысл поставленной задачи

Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи

Проявляют мотивацию к познавательной деятельности при решении задач с практическим содержанием

Демонстрируют мотивацию к познавательной деятельности

Проявляют интерес к креативной деятельности, активности при подготовке иллюстраций изучаемых понятий

Осознают роль ученика, осваивают личностный смысл учения

Демонстри руют математические знания и умения при решении и задач

Используют изученные свойства геометрических фигур и отношения между ними при решении задач на вычисление и доказательство

Уметь объяснять, что такое условие и заключение теоремы

П:восстанавливают предметную ситуацию, описанную в задаче, переформулируют условие, извлекать необходимую информацию

Р:оценивают степень и способы достижения цели в учебных ситуациях, исправляют ошибки с помощью учителя

К:формулируют собственное мнение и позицию, задают вопросы, слушают собеседника

П:строят логически обоснованное рассуждение, включающее установление причинно-следственных связей

Р:работая по плану, сверяют свои действия с целью, вносят корректировки

К:сотрудничают с одноклассниками при решении задач; умеют выслушать оппонента. Формулируют выводы

П:обрабатывают информацию и передают ее устным, письменным, графическим и символьным способами

Р:критически оценивают полученный ответ, осуществляют самоконтроль, проверяя ответ на соответствие условию

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;

Проверь себя! (выбери верное утверждение).

А1. В треугольнике сумма углов равна 210°?

1) да; 2) нет; 3) возможно.

А2. Существует треугольник с углами:

1) 10°,60°,90°; 2) 30˚, 60˚, 90˚; 3) 46˚, 160˚, 4˚; 4) 100˚, 20˚, 55˚

А3. Углы равностороннего треугольника

равны по: 1) 70°; 2) 90°; 3) 60°; 4) 180°.

А4. В треугольнике могут быть: 1) 3 острых угла;

2) 1 острый угол, 1 прямой угол, 1 тупой угол; 3) 2 тупых угла и 1 острый;

4) 2 прямых угла и 1 острый;