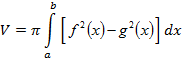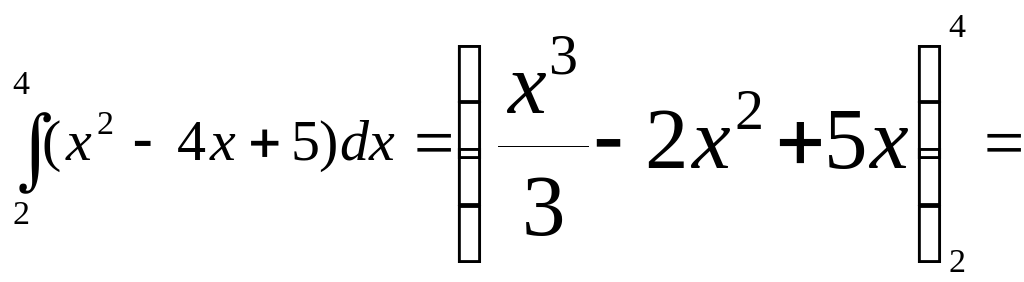Ашық сабақ "Қисық сызықты трапеция"

Сабақ: Алгебра

Мектеп: «Тұрағұл Қоңыр атындағы орта мектеп-балабқша » КММ

Күні:

Мұғалімнің есімі: Тезекова Гульнур Саулехановна

Сынып: 11

Қатысқандар: Қатыспағандар:

Тақырыбы

Қисықсызықты трапецияның ауданы

Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)

Алғашқы функция және анықталмаған интегралдардың формулаларын пайдаланып қисықсызықты трапецияның ауданын табу.

Сабақтың мақсаты

Барлық оқушылар: Алғашқы функция және анықталмаған интегралдардың формулаларын пайдаланып қисықсызықты трапецияның ауданын табуалгоритм біледі.

Оқушылардың басым бөлігі: Есеп шығаруда формулаларды қолдана алады.

Кейбір оқушылар: Есептерді талдай алады.

Бағалау критерийі

Алғашқы функция және анықталмаған интег-ралдардың анықтамасы мен формулаларын пайдаланып қисықсызықты трапецияның ауданын табуды білу.

Есеп шығаруда формулаларды қолдану.

Тілдік мақсат

Математикалық тілде айта алады: Алғашқы функция және анықталмаған интегралдар, қисықсызықты трапеция ауданын табуда формулаларды қолдана алады.

Құндылықтарға баулу

Оқушыларды бір-бірін сыйлауға, құрметтеуге, тыңдай білуге тәрбиелеп, көсбашылыққа ұмтылдыру.

Пәнаралық байланыс

Геометриялық есептерде интегралды қолдана алады.

Тақырып бойынша алдыңғы білім

Функция. Функция түрлері мен қасиеттері. Туынды. Туындыны қолдану. Алғашқы функция және анықталмаған интеграл формулалары.

Сабақ барысы

Жоспарланған кезеңдер

Жоспарланған жаттығу түрлері

Ресурстар

Басталуы

(10мин)

Ортасы

Аяқталуы

Ұйымдастыру: «Шаттық шеңбер» құру, тілек айтып, топқа бөлу:

1.«Функция»

2.«Туынды»

3.«Интеграл»

Үй тапсырмасын тексеру:

Үйге берілген тапсырманы өзара тексеруді ұйымдастыру.

Үй тапсырмасының дұрыс шешімі интербелсенді тақтада көрсетіледі.

«Құпия зат»

Алғашқы функция және анықталмаған интеграл формулаларын сұрау.

«Мұғалім шолуы»

Алғашқы функция және анықталмаған интеграл формулаларын пайдаланып қисықсызықты трапецияның ауданын табуалгоритм түсіндіру, есептер шығару.

S=F(b) - F(a) - қисықсызықты трапецияның ауданын табу формуласы.

Есептер шығару: №18,19(1,3),24(1,3,5,7)

«Жалғыз аяқ жол»

Алғашқы функция және анықталмаған интеграл формулалары.

Қисықсызықты трапеция ауданын табудың алгоритмі.

Жаңа білімге қатысты интербелсенді тақтада сызбалар ұсынып, пікіраласу жүргізеді (модульдер: СТО, ДО, АКТ)

Сызбалар арқылы жаңа білім геометриямен байланысын тауып, оның 4 аксиомасы орындалатынын байқайды. Анықтамасын тұжырымдап, оқулықтағы 4-9 суреттерден қисық сызықты трапецияны әр түрлі функцияның графигі арқылы алуға болатынын түсінеді.

А) Қисықсызықты трапеция ұғымымен таныстыру.

Анықтама: Үзіліссіз, y=f(x), f(x)0 функциясының графигімен, абсцисса осімен және x=a. x=b түзулерімен шектелген жазық фигура қисықсызықты трапеция деп аталады.

Ә) Қисықсызықты трапецияның ауданын есептеу формуласын қорытып шығару. (S=F(b)-F(a))

Б) Қисықсызықты трапецияның табанымен таныстыру. (қисықсызықты трапецияның табаны ретінде алынатын [a;b] кесіндісі)

В) Қисықсызықты трапецияның ауданын есептейтін алгоритімен таныстыру.

1. Бір координаталық жазықтықта берілген қисықтардың графиктерін салу;

2.Графигі жоғарыдан қисықсызықты трапецияны шектейтін функцияның алғашқы функцияларының бірін анықтау;

3.Қисықсызықты трапецияның төменгі табаны болатын кесіндінің шеткі нүктелерінің координаталарын анықтау;

4. S=F(b)-F(a) формуласы бойынша қисықсызықты трапецияның ауданын есептеу

Берілген сызықтармен шектелген фигураның ауданын табу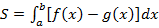

_{ } формуласы арқылы табылады.

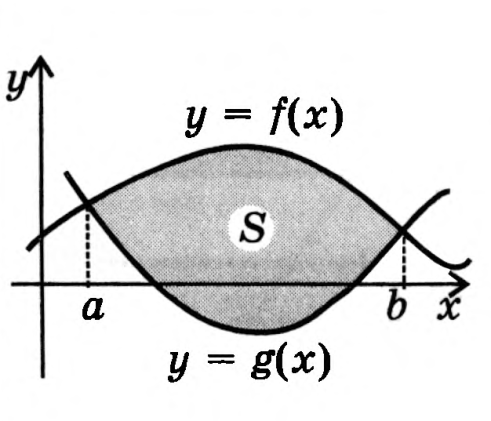Көлем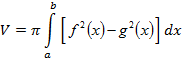

1. Практикалық жұмыстар.

2. Практикалық жұмыстар.

Берілген қисықтармен шектелген фигураның ауданын табыңдар:

1. Боялған фигураның ауданын табыңыз.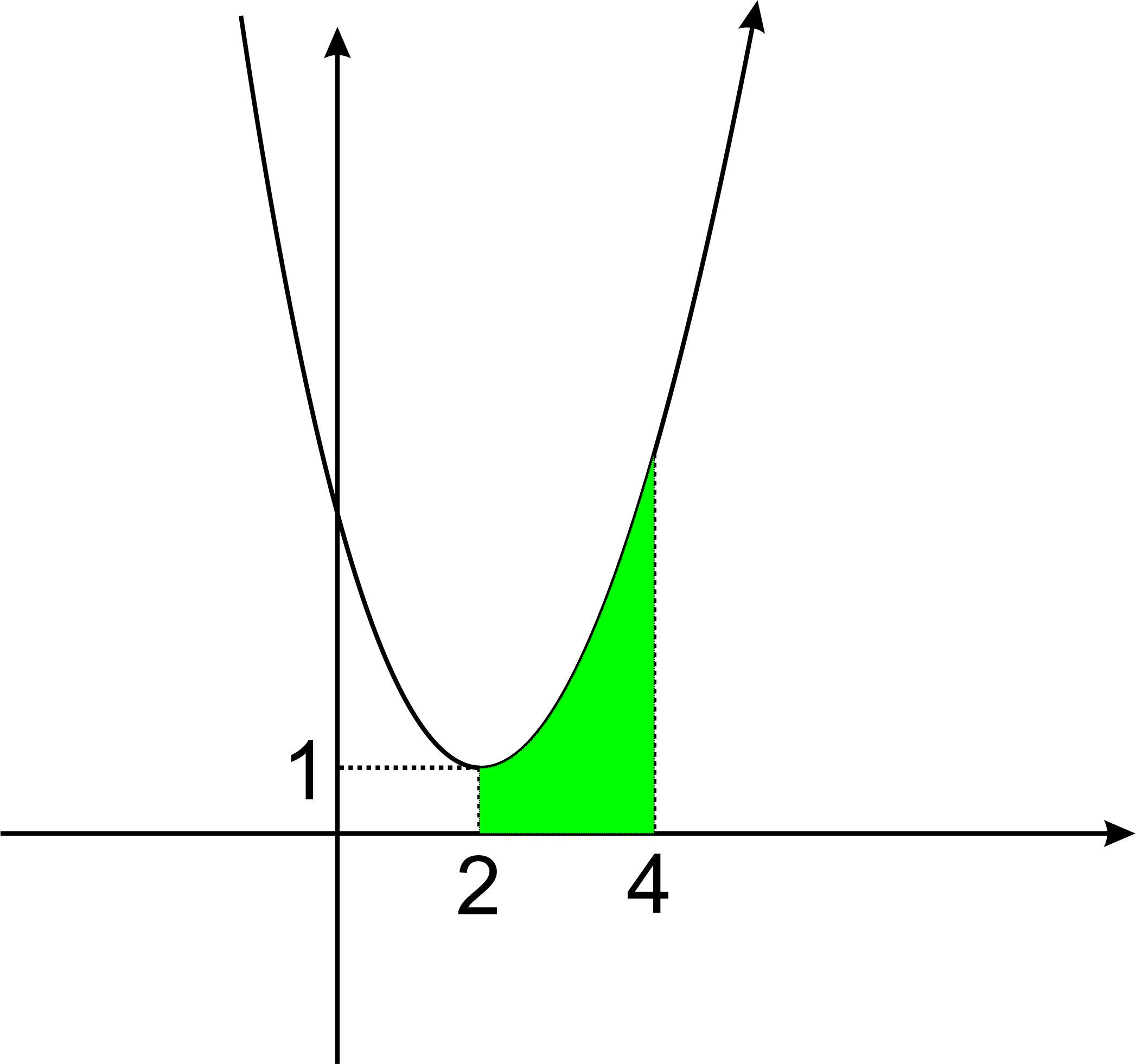

Шешімі: y=(x-2)² +1

=x²-4x+4+1

= x²-4x+5

Аудан :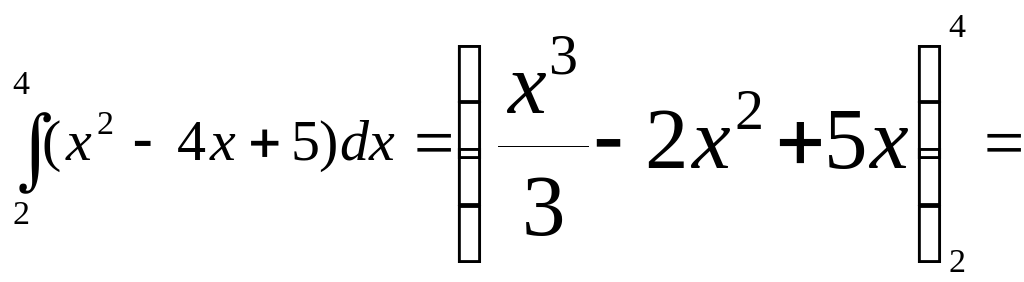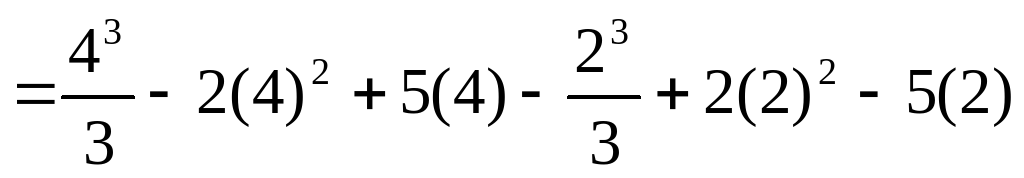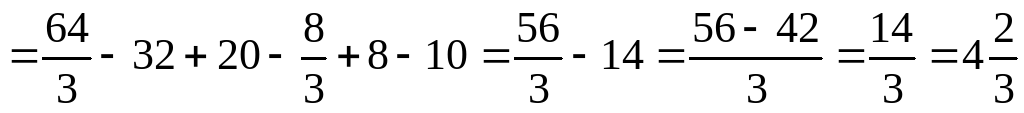

Деңгейлік тапсырмалар:

1-деңгей

1.f`(х)=х2-х+4, у=0, х=-1, х=0 қисықтарымен шектелген қисықсызықты трапецияның ауданын табыңдар.

2. y=0, y=x2+2, x=1, х=0 қисықтарымен шектелген фигураның ауданын есептеу формуласын жазыңдар.

3.f`(х)=х2-1 параболасы және у=0, х=3 түзулерімен шектелген қисықсызықты трапецияның ауданын табыңдар.

2-деңгей

1.у=х2+3, х=-1, х=0, у=0 қисықтарымен шектелген фигураның ауданын есептеңдер.

2. y=0, y=x2+4, x=1, x=0 қисықтарымен шектелген фигураның ауданын есептеу формуласын жазыңдар.

7.Өз бетімен орындауға арналған тапсырмалар

y=x3, y=0, x=2 сызықтарымен шектелген фигураның ауданын табыңыз.

4 B) 12 C) 1 D) 5 E) 6

Мына сызықтармен шектелген фигураның ауданын табыңыз.

y=√x, x=1, x=4

12/3 B) 72/3 C) 2/3 D) 42/3 E) 3

Жинаған балдары арқылы жиынтық бағалау

Үйге тапсырма:№18,19(2,4),24(2,4,6,8)

Алгебра және анализ бастамалары 11

Электронды оқулық

Плакат, пламастр, стикер,клей,қайшы т.б.

Қосымша ақпарат:

Саралау – Сіз қандай тәсілмен көбірек қолдау көрсетпексіз? Сіз басқаларға қарағанда қабілетті оқушыларға қандай тапсырмалар бересіз?

Бағалау – сіз оқушылардың материялды игеру деңгейін қалай тексеруді жоспарлап отырсыз?

Денсаулық және қауіпсіздік техникасын сақтау

Үлгерімі төмен оқушыларға ЖАДА ұйымдастыру арқылы деңгейлік тапсырмалар беремін.

Қабілеті жоғары оқушыларға жоғары дәрежелі сұрақтар қоямын.

(Оқушылардың ой-пікірлерін тыңдау, қарым-қатынас мәдениеттілігін ұстануларына түрткі болу, тапқырлық танытуын мадақтау, оқушының ерекше іс-қимылына лайықты мадақтаулар айту, есептің шешімін табуда тығырыққа тірелген оқушыға қолдау көрсету...)

• Бағалау критерийлері

• Бірін-бірі бағалау

• Топты бағалау

• Өзін-өзі бағалау

• Бағалау парақшалары

• Кері байланыс

Интерактивті тақтаны тек уақытты үнемдеу үшін пайдаланамын, электронды оқулық көрсетемін.

Әрбір оқушының сабақтағы денсаулығына әсер етпейтіндей етіп отырғыза отырып, жұмыс жасауына мүмкіндік беру

Рефлекcия

Сабақ оқу мақсаттары шынайы ма?

Бүгін оқушылар не білді?

Сыныптағы ахуал қандай болды?

Мен жоспарлаған саралау тиімді болды ма?

Мен берілген уақыт ішінде үлгердім бе?

Мен өз жоспарыма қандай түзетулер енгіздім және неліктен

Қорытынды бағамдау:

Қандай екі нәрсе табысты болды (оқытуды да, оқуды да ескеріңіз)? _______________________________________

____________________________________________________________________________________________

Қандай екі нәрсе сабақты жақсарта алды?

________________________________________________________

____________________________________________________________________________________________

Сабақ барысында мен сынып немесе жекелеген оқушылар туралы менің келесі сабағымды жетілдіруге көмектесетін не білдім?

_______________________________________________________________________________ ____________________________________________________________________________________________

Сынып: 11

Қатысқандар саны:

қатыспағандар:

Сабақ тақырыбы

Қисықсызықты трапеция. Қисықсызықты трапецияның ауданы

Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына

сілтеме)

Сабақ мақсаты

Дәл жоғарғы және дәл төменгі шен, қисық сызықты трапеция ауданы туралы ұғымды және қисықтармен шектелген қисық сызықты трапецияны кескіндей білу.

Алғашқы функция ұғымын қолдану арқылы, қисық сызықты трапеция ауданын табу біліктілігін мен қисықтармен шектелген қисық сызықты трапецияны кескіндеуді меңгеру.

Бағалау критерийлері

Алғашқы функция және анықталмаған интег-ралдардың анықтамасы мен формулаларын пайдаланып қисықсызықты трапецияның ауданын табуды біледі.

Есеп шығаруда формулаларды қолданады.

Тілдік мақсаттар

Оқушылар:

Математикалық тілде айта алады: Алғашқы функция және анықталмаған интегралдар, қисықсызықты трапеция ауданын табуда формулаларды қолдана алады.

Пәндік лексика және терминология

Теру/комбинация, орын алмастыру, n-нен r элемент таңдау, орналастыру, рет, реттеу, орын ауыстыру.

Диалог/хат үшін пайдалы фразаларсериясы

Қисық сызықты трапеция деп қандай фигураны айтамыз?

2)      Оның ауданын қандай формуламен табамыз?

3)      Шектері берілмесе, оны қалай табуға болады?

4)      Қандай жағдайда аудан теріс мәнге ие болады, оны қалай есептейміз?

Құндылықтарды

дарыту (оның ішінде жаhандық азаматтылықтың негізгі элементтері

(ЖА)

- өмір бойы оқыту (сабақтың бүкіл мазмұны ойынша);

- жауапкершілік, сыйластық (топтық жұмыс арқылы);

- адалдық (топтағы бір-бірін бағалау арқылы);

- үштілдік (сабақ мазмұны арқылы);

- әрекеттестік, шыдамдылық(топтық жұмыс, сабақ мазмұны арқылы);

- денсаулық (кабинеттің санитарлық жағдайы).

Негізгі дағды

Өзінбасқарудағдылары (іс-әрекетжоспарынжәнебағалаукритерийлерінқұруарқылы)

АКТ қолдану дағдылары

Интерактивті тақтаның мүмкіндіктері, Интернет ресурстары.

Сабақ барысы

Жоспарлан

ған сабақ кезеңдері

Сабақта жоспарланған жұмыс

Ресурстар

Сабақтың басы

3 мин

1. Ұйымдастыру кезеңі. Амандасу.

Оқытудың тақырыбы және мақсаты, жетістік критерийі

Мұғалім оқушыларға сабақ мақсатына сүйеніп өздігінен бағалау критерийін жасауға ұсынады

Критерийлерді бірге талдау, негізгі критерийлерді тақтаға жазу

Топтарға сұрақтар:

1. 1- топтың аты қалай аталады? (Сызықтық функция)

Графигі қалай аталады? (Түзу сызық)

2.- топтың аты қалай аталады? (квадраттық функция)

Графигі қалай аталады? (парабола)

1. 3- топтың аты қалай аталады? (кері пропорционалдық функция)

Графигі қалай аталады? (гипербола)

1. Енді осы жұмысымызды бағалайтын топ координаторларын сайлайық. Ол топ мүшелеріне тапсырма беріп, олардың жұмысын сабақ бойы бақылап, әрқайсысын бағалап отырады.

Әр тапсырманы бағалаудың критерийлері берілген. Олар әр топтың алдында бар.

Топпен жұмыс істеу ережесін білеміз, осы ережені сақтауымыз керек.

Егер сендер мына ребусты дұрыс шешсеңдер, біздің бүгінгі сабағымыздың тақырыбы айқындалады.Бүгінгі сабағымыз басқа сабақтардан өте ерекше болмақ. Біз, қисық сызықты трапецияның ауданын табуға арналған есептерді шешеміз.

1. Сабақтың тақырыбын және мақсатын айту.

2. Ребус шешу арқылы оқушылар сабақтың мақсатын өздері айқындайды.

Площадь---------Аудан--------- Area

Сабақтың ортасы

Диалогтық оқыту

Оқушылар жұпта жұмыс жасайды.Өздерін тексереді. Қажеттілік бойынша қиындық туғызған есепті тақтада талдайды

1-топқа: Функция және графиктері.

2-топқа: Алғашқы функцияны табу ережелері.

3- топқа: Мына фигуралар қисық сызықты трапеция бола ма?

Осы тапсырмаға- 5мин уақыт беріледі, оны қорғауға – 1мин беріледі,

барлығына – 8 мин уақыт беріледі.

Жинақталып, тиімді әдіс- тәсілдерді қолданып, уақытты үнемдеп, барлық алған білімдеріңді тиімді қолдануларыңды сұраймын.

Әр топ өз тапсырмасын орындайды.

1. топ:

у=_{ }, у=0, х=4 сызықтарымен шектелген фигураның ауданын табыңдар.

1. топ:

у=х³, у=0, х=2 сызықтарымен шектелген фигураның ауданын табыңдар.

1. топ:

у=4-х², у=0 сызықтарымен шектелген фигураның ауданын табыңдар

Сабақ соңы

2 мин

РефлексияОқушылар стикерлерде өздерінің сабақ мақсатына жетулерін бағалапЖ және Ұ әріптерін қояды.

Үй жұмысы:

Қосымша

Саралау –оқушыларға көбірек қолдау көрсетуді қалай жоспарлайсыз? Қабілетіжоғарыоқушыларғақандайміндетқоюдыжоспарлапотырсыз?

Бағалау – оқушылардыңматериалдымеңгерудеңгейінтексерудіқалайжоспарлайсыз?

Денсаулық және қауіпсіздікті сақтау ережесі

Сабақбойыншарефлексия

Сабақмақсаттары/оқумақсаттарыдұрысқойылғанба? ОқушылардыңбарлығыОМқолжеткіздіме?

Жеткізбесе, неліктен?

Сабақтасаралаудұрысжүргізілдіме?

Сабақтыңуақыттықкезеңдерісақталдыма?

Сабақжоспарынанқандайауытқуларболды, неліктен?

Бұлбөлімдісабақтуралыөзпікіріңіздібілдіруүшінпайдаланыңыз. Өзсабағыңызтуралысолжақбағандаберілгенсұрақтарғажауапберіңіз.

Жалпыбаға

Сабақтыңжақсыөткенекіаспектісі (оқытутуралыда, оқутуралыдаойланыңыз)?

1:

2:

Сабақты жақсартуға не ықпал ете алады (оқыту туралы да, оқу туралы да ойланыңыз)?

1:

2:

Сабақ барысында сынып туралы немесе жекелеген оқушылардың жетістік/қиындықтары туралы нені білдім, келесі сабақтарда неге көңіл бөлу қажет?