Презентация по геометрии "Многогранники"

Многогранники

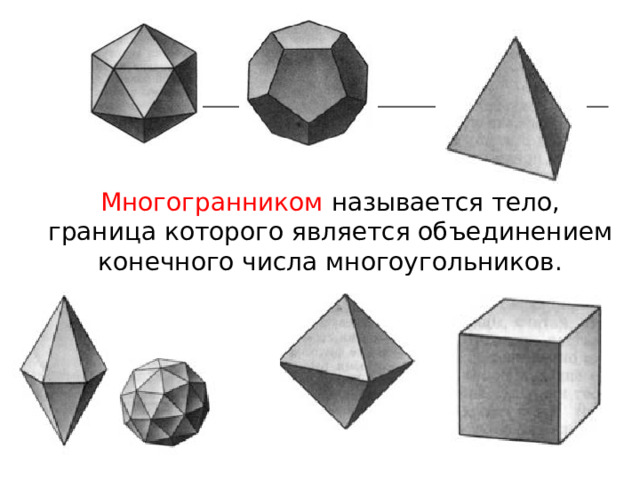
Многогранником называется тело, граница которого является объединением конечного числа многоугольников.

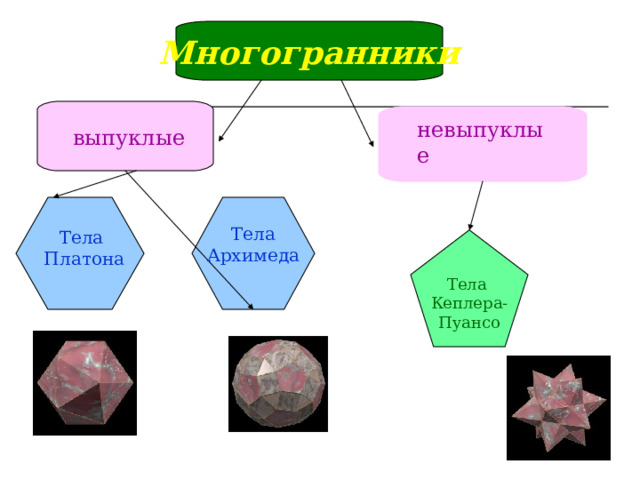
Многогранники

выпуклые

невыпуклые

Тела

Архимеда

Тела

Платона

Тела

Кеплера-

Пуансо

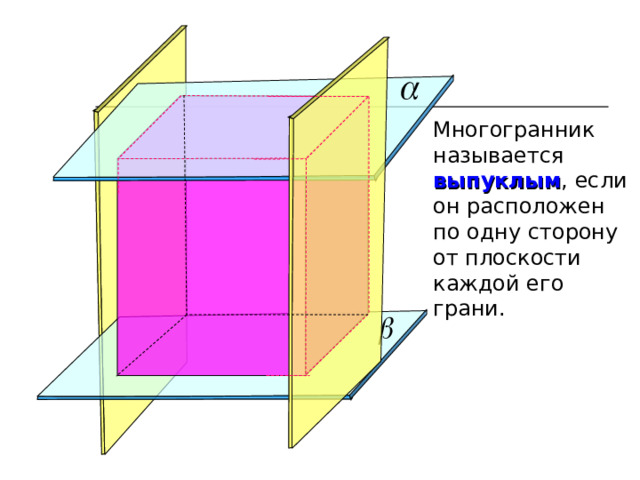
Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани.

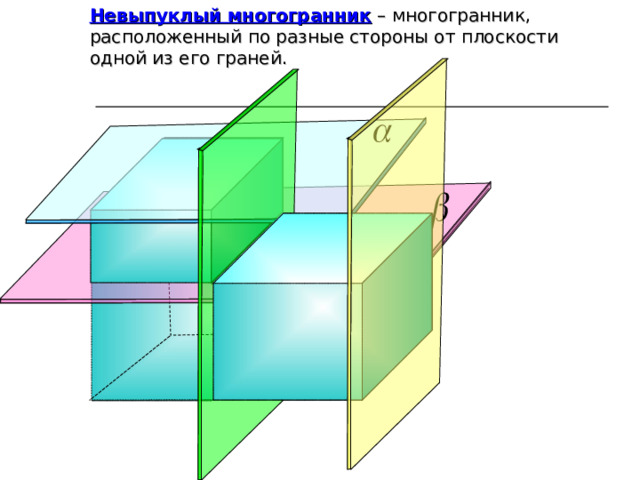
Невыпуклый многогранник – многогранник, расположенный по разные стороны от плоскости одной из его граней.

Г.В. Дорофеев, Л.Г. Петерсон, 6 класс (часть 3 ). № 7 42 ( а)

4

Правильными многогранниками

называют выпуклые многогранники, все грани и все углы которых равны, причем грани - правильные многоугольники .

4

Правильные многогранники

Сколько же их существует?

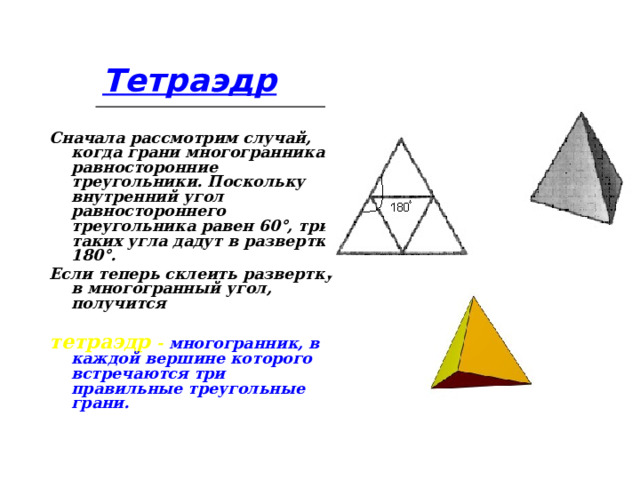
Тетраэдр

Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°.

Если теперь склеить развертку в многогранный угол, получится

тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани.

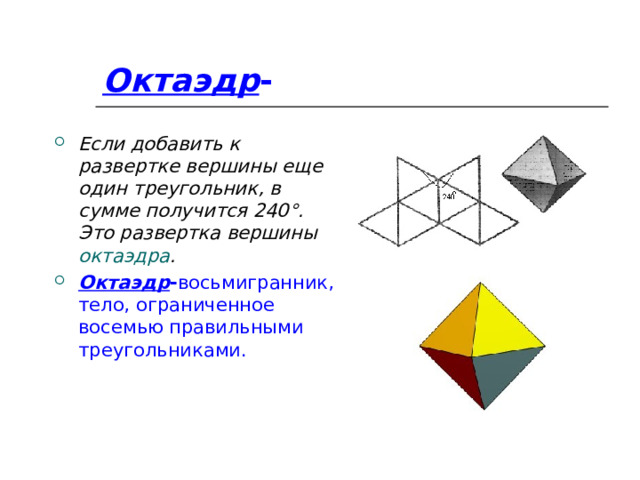
Октаэдр -

• Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра .
• Октаэдр - восьмигранник, тело, ограниченное восемью правильными треугольниками.

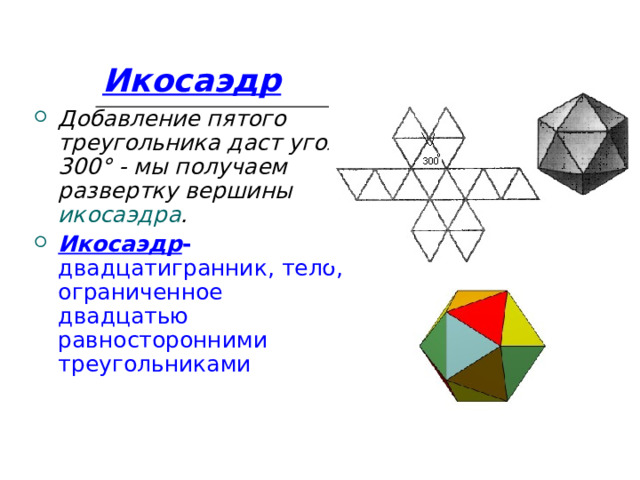
Икосаэдр

• Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра .
• Икосаэдр - двадцатигранник, тело, ограниченное двадцатью равносторонними треугольниками

Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.

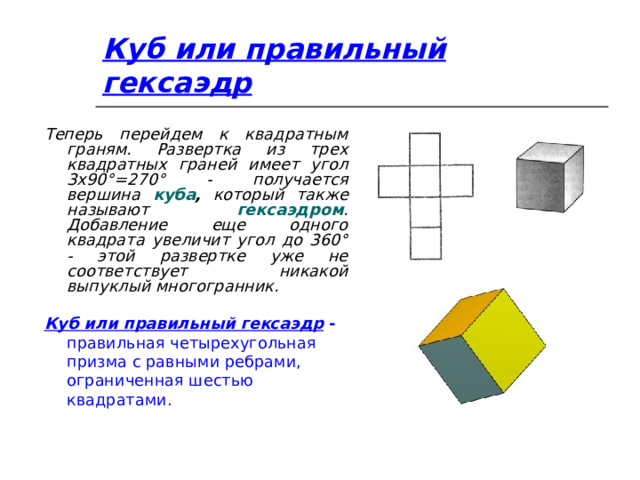
Куб или правильный гексаэдр

Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба , который также называют гексаэдром . Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.

Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами.

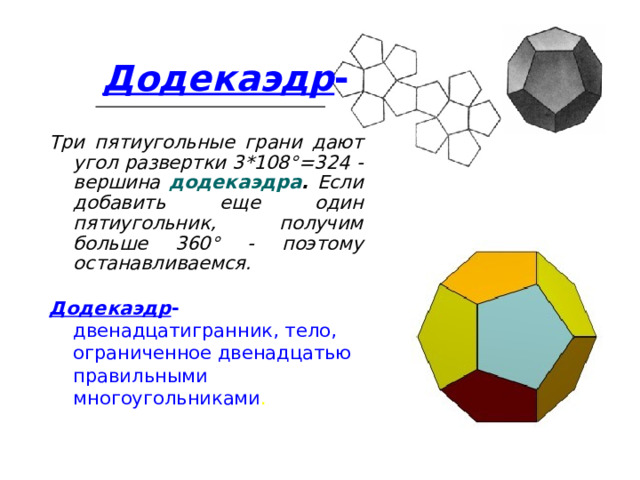
Додекаэдр -

Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра . Если добавить еще один пятиугольник, получим больше 360° - поэтому останавливаемся.

Додекаэдр - двенадцатигранник, тело, ограниченное двенадцатью правильными многоугольниками .

Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.

Сделаем вывод:

• Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр , октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
• Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
• «эдра» - грань
• «тетра» - 4
• «гекса» - 6
• «окта» - 8
• «икоса» - 20
• «додека» - 12

Тетраэдр

Октаэдр

Гексаэдр

Икосаэдр

Додекаэдр

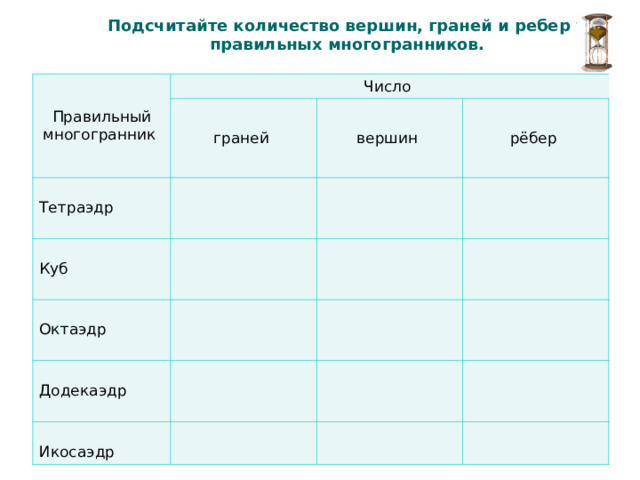
Подсчитайте количество вершин, граней и ребер у правильных многогранников.

Правильный многогранник

Число

Тетраэдр

граней

Куб

вершин

рёбер

Октаэдр

Додекаэдр

Икосаэдр

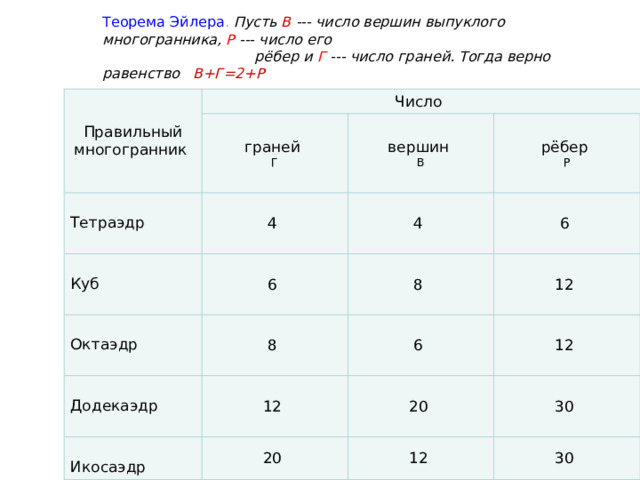
Теорема Эйлера . Пусть В --- число вершин выпуклого многогранника, Р --- число его рёбер и Г --- число граней. Тогда верно равенство В+Г=2+Р

Правильный многогранник

Число

граней

Г

Тетраэдр

Куб

вершин

В

4

Октаэдр

6

4

рёбер

Р

6

8

Додекаэдр

8

12

12

6

Икосаэдр

12

20

20

30

12

30

Историческая справка

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком

пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.

Эти тела еще называют телами Платона

Платон связал с этими телами формы атомов основных стихий природы.

тетраэдр

огонь

икосаэдр

вода

воздух

октаэдр

гексаэдр

земля

вселенная

   додекаэдр

Дальнейшее развитие математики связано с именами

Платона, Евклида, Архимеда, Кеплера

Все использовали в своих философских теориях

правильные многогранники.

Тела Архимеда

Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.

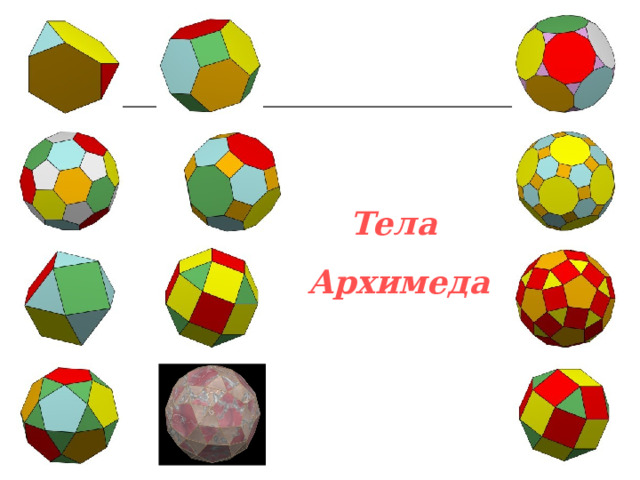
Тела

Архимеда

25

Тела

Кеплера - Пуансо

Среди невыпуклых однородных многогранников существуют аналоги платоновых тел - четыре правильных невыпуклых однородных многогранника или тела Кеплера - Пуансо.

Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники , все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.

25

Большой звездчатый

додекаэдр

Малый звездчатый

додекаэдр

Большой икосаэдр

25

Многогранники в архитектуре

Великая пирамида в Гизе . Эта грандиозная Египетская пирамида является древнейшим из Семи чудес древности.   Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц.

        Некоторые археологи считают, что, возможно, на строительство Великой пирамиды 100 000 человек потребовалось 20 лет. Она была создана из более чем 2 миллионов каменных блоков, каждый из которых весил не менее 2,5 тонн.  

29

Многогранники в архитектуре Москвы

Собор непорочного зачатия

Девы Марии

на малой Грузинской

Исторический музей

Многогранники в архитектуре Москвы

Новоарбатский замок

Малый Ржевский пер.

Многогранники в архитектуре Москвы

Казанская церковь в Москве

Александрийский маяк .

    Маяк был построен на маленьком острове Фарос в Средиземном море, около берегов Александрии. Этот оживленный порт основал Александр Великий во время посещения Египта. Сооружение назвали по имени острова. На его строительство, должно быть, ушло 20 лет, а завершен он был около 280 г. до н.э., во времена правления Птолемея II, царя Египта.

Три башни

Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.

Многогранники в искусстве

Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.

29

Голландский художник Мориц Корнилис Эшер (1898-1972)создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

29

Применения икосаэдров

Титульный лист книги Ж. Кузена «Книга о перспективе».

Надгробный памятник в кафедральном соборе Солсбери.

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра.

Форму додекаэдра, по мнению древних, имела  ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности  правильного додекаэдра.

29

Чудо природы – кристаллы

Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников:

• куб передает форму кристаллов поваренной соли NaCl
• монокристалл алюминиево-калиевых квасцов имеет форму октаэдра,
• кристалл сернистого колчедана FeS имеет форму додекаэдра,
• сернокислый натрий - тетраэдр,
• бор - икосаэдр.

Многогранники в природе

• Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.

Кристалл сульфата меди II

Кристалл алюмокалиевых

квасцов

Кристалл сульфата никеля II

Пчёлы

строили свои шестиугольные соты

задолго до появления человека.

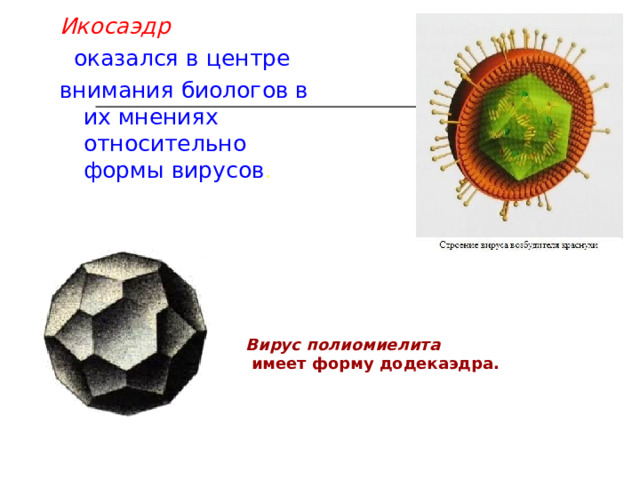
Икосаэдр

оказался в центре

внимания биологов в их мнениях относительно формы вирусов .

Вирус полиомиелита

имеет форму додекаэдра.

Многогранники в химии

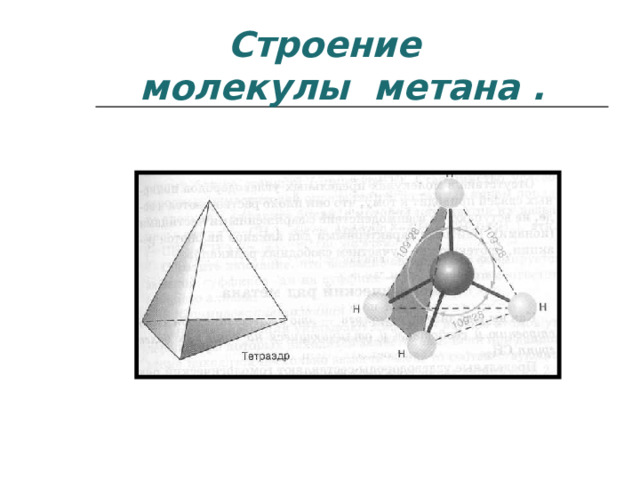
Строение молекулы метана .

Правильные многогранники встречаются в живой природе.

Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр .

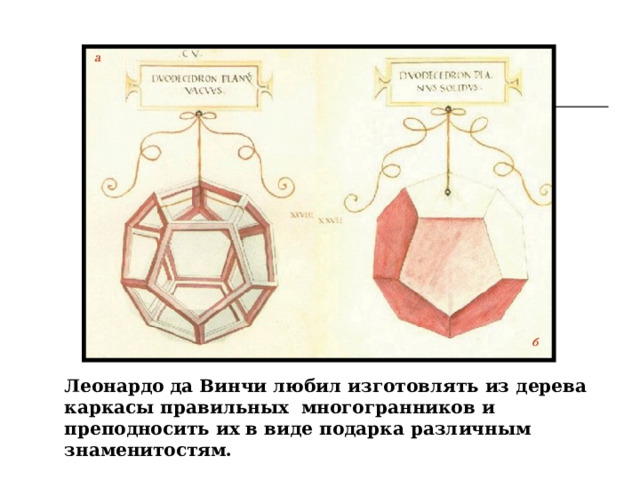
Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка различным знаменитостям.

Изящный пример звездчатого додекаэдра можно найти в его работе "Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.

Наиболее интересная работа Эшера - гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров.

Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры.

ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»

Правильная форма алмаза.

Обязательно попробуй!

Кубик Рубика- головоломка

А теперь проверьте свои знания по изученному материалу

Тестирование.

1. Поверхность, составленная из четырех треугольников

А) ТЕТРАЭДР

B) ПАРАЛЛЕЛЕПИПЕД

С) КВАДРАТ

D ) ШАР

2. Поверхность, составленная из многоугольников и ограничива- ющая некоторое геометрическое тело

А) МНОГОУГОЛЬНИК

B) МНОГОГРАННИК

С) ТРЕУГОЛЬНИК

D ) КВАДРАТ

3. Многоугольник, из которого составлен многогранник

А) СТОРОНА

B) РЕБРО

С) ГРАНЬ

D ) ВЕРШИНА

4. Отрезок, соединяющий две вершины, не принадлежащие одной грани

А) ДИАГОНАЛЬ

B) МЕДИАНА

С) ВЫСОТА

D ) АПОФЕМА

5. Высота боковой грани правильной пирамиды, проведенная из ее вершины

А) ДИАГОНАЛЬ

B) АПОФЕМА

С) КАТЕТ

D ) ГИПОТЕНУЗА

6. Этот правильный многогранник составлен из 8-ми равносторонних треугольников

А) КВАДРАТ

B) ТЕТРАЭДР

С) ДОДЕКАЭДР

D ) ОКТАЭДР

7. Составлен из 6-ти правильных четырехугольников

А) КВАДРАТ

B) ТЕТРАЭДР

С) КУБ

D ) ПИРАМИДА

8. Стихия тетраэдра

А) ВОДА

B) ВОЗДУХ

С) ЗЕМЛЯ

D ) ОГОНЬ

9. Многоугольник, подобный пчелиным сотам

А) 8-МИ УГОЛЬНИК

B) 6-ТИ УГОЛЬНИК

С) 4-Х УГОЛЬНИК

D ) ТРЕУГОЛЬНИК

Проверь себя.

1. A

2. B

3. C

4. A

5. B

6. D

7. C

8. D

9. B

6

в

е

р

ы

т

е

ч

1

2

с

2

к

и

н

ь

т

л

я

г

у

и

п

о

т

о

5

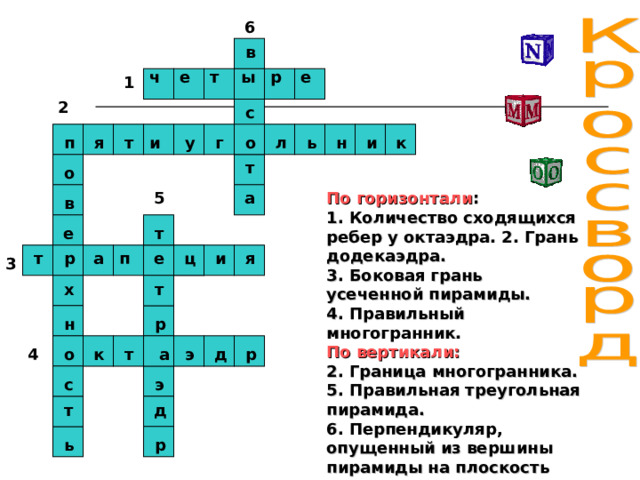
По горизонтали : 1. Количество сходящихся ребер у октаэдра. 2. Грань додекаэдра.

а

3. Боковая грань усеченной пирамиды.

4. Правильный многогранник.

По вертикали: 2 . Граница многогранника.

5 . Правильная треугольная пирамида.

6 . Перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

в

т

е

я

и

ц

е

а

р

т

п

3

т

х

р

н

4

э

а

р

д

о

к

т

э

с

т

д

р

ь

о