Разработка рабочей программы по геометрии 9 класс

Название раздела

Предметные результаты

Метапредметные результаты

Личностные результаты

Ученик научится

Ученик получит возможность научится

«Векторы»

Обозначать и изображать векторы,

изображать вектор, равный данному.

Строить вектор, равный сумме двух векторов, используя правила треугольника, параллелограмма. Формулировать законы сложения, строить сумму нескольких векторов, используя правило многоугольника,

строить вектор, равный разности двух векторов, двумя способами.

Решать геометрические задачи использование алгоритма выражения через данные векторы, используя правила сложения, вычитания и умножения вектора на число.

Решать простейшие геометрические задачи, опираясь на изученные свойства векторов,

Находить среднюю линию трапеции по заданным основаниям.

В повседневной жизни и при изучении других предметов:

использовать векторы для решения простейших задач на определение скорости относительного движения.

Овладеть векторным методом для решения задач на вычисление и доказательство.

Прибрести опыт выполнения проектов.

1.Умение самостоятельно планировать альтернативные пути         достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.

2.Умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы.

3.Умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения.

4.Осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей.

5.Умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы.

6.Умение создавать,         применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;

7.Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё         мнение.

8.Формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности).

9.Первоначальные представления об идеях и о методах математики как об универсальном языке         науки и техники, о средстве моделирования явлений и процессов.

10.Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.

11.Умение находить в         различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации.

12.Умение понимать и         использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации.

13.Умение выдвигать         гипотезы при решении учебных задач и         понимать необходимость их проверки;

14.Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

15.Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

16.Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.

17.Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.

Регулятивные УДД

определять цель деятельности на уроке с помощью учителя и самостоятельно;

учиться совместно с учителем обнаруживать и формулировать учебную проблему; учиться планировать учебную деятельность на уроке; высказывать свою версию, пытаться предлагать способ её проверки (на основе продуктивных заданий в учебнике);работая по предложенному плану, использовать необходимые средства (учебник, компьютер и инструменты); определять успешность выполнения своего задания в диалоге с учителем. Средством формирования регулятивных действий служат технология проблемного  диалога на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).

       Познавательные УУД

ориентироваться в своей системе знаний: понимать, что нужна дополнительная информация (знания) для решения учебной задачи в один шаг; делать предварительный отбор источников информации для решения учебной задачи; добывать новые знания: находить необходимую информацию, как в учебнике, так и в предложенных учителем словарях, справочниках и интернет - ресурсах; добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.);перерабатывать полученную информацию: наблюдать и делать самостоятельные выводы. Средством формирования познавательных действий служит учебный материал и задания учебника, обеспечивающие первую линию развития – умение объяснять мир.

        Коммуникативные УДД

доносить свою позицию до других: оформлять свою мысль в устной и письменной речи (на уровне предложения или небольшого текста); слушать и понимать речь других; выразительно читать и пересказывать текст; вступать в беседу на уроке и в жизни; совместно договариваться о правилах общения и поведения в школе и следовать им; учиться выполнять различные роли в группе (лидера, исполнителя, критика).Средством формирования коммуникативных действий служат технология проблемного диалога (побуждающий и подводящий диалог), технология продуктивного чтения и организация работы в малых группах.

1.Формирование ответственного отношения к учению,        готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов.

2.Формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики.

3.Формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной,         общественно полезной, учебно-исследовательской, творческой и других видах деятельности.

4.Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать         аргументацию, приводить примеры и контрпримеры.

5.Критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта.

6.Креативность мышления, инициативу, находчивость,         активность при решении геометрических задач.

7.Умение контролировать процесс и результат учебной математической деятельности.

8.Способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

«Метод координат»

Оперировать на базовом уровне понятиями координаты вектора, координаты суммы и разности векторов, произведения вектора на число.

Вычислять координаты вектора, координаты суммы и разности векторов, координаты произведения вектора на число.

Вычислять угол между векторами,

вычислять скалярное произведение векторов.

Вычислять расстояние между точками по известным координатам,

вычислять координаты середины отрезка.

Составлять уравнение окружности, зная координаты центра и точки окружности, составлять уравнение прямой по координатам двух ее точек;

решать простейшие задачи методом координат

Овладеть координатным методом решения задач на вычисление и доказательство.

Приобрести опыт использования компьютерных программ для анализа частных случаев

взаимного расположения окружностей и прямых.

Приобрести опыт выполнения проектов

«Соотношения между сторонами и углами треугольника. Скалярное

произведение векторов»

Оперировать на базовом уровне понятиями: синуса, косинуса и тангенса углов,

применять основное тригонометрическое тождество при решении задач на нахождение одной тригонометрической функции через другую.

Изображать угол между векторами, вычислять скалярное произведение векторов,

находить углы между векторами, используя формулу скалярного произведения в координатах.

Применять теорему синусов, теорему косинусов,

применять формулу площади треугольника: S = ,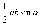

решать простейшие задачи на нахождение сторон и углов произвольного треугольника.

Вычислять площади фигур, составленных из двух и более прямоугольников, параллелограммов, треугольников, круга и сектора.

Вычислять площади многоугольников, используя отношения равновеликости и равносоставленности.

Применять алгебраический и тригонометрический материал при решении задач на вычисление площадей многоугольников.

Приобрести опыт применения алгебраического и тригонометрического аппарата при решении геометрических задач

«Длина окружности и площадь круга»

Оперировать на базовом уровне понятиями правильного многоугольника. Применять формулу для вычисления угла правильного n-угольника. Применять формулы площади, стороны правильного многоугольника, радиуса вписанной и описанной окружности, применять формулы длины окружности, дуги окружности, площади круга и кругового сектора. Использовать свойства измерения длин, углов при решении задач на нахождение длины отрезка, градусной меры угла. Вычислять площади треугольников, прямоугольников, трапеций, кругов и секторов. Вычислять длину окружности и длину дуги окружности. Вычислять длины линейных элементов фигур и их углы, используя изученные формулы.

В повседневной жизни и при изучении других предметов: решать практические задачи, связанные с нахождением геометрических величин.

выводить формулу для вычисления угла правильного n-угольника и применять ее в процессе решения задач,

проводить доказательства теорем о формуле площади, стороны правильного многоугольника, радиуса вписанной и описанной окружности и следствий из теорем и применять их при решении задач,

решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур.

«Движения»

Оперировать на базовом уровне понятиями отображения плоскости на себя и движения.

Оперировать на базовом уровне понятиями осевой и центральной симметрии, параллельного переноса, поворота.

Распознавать виды движений,

выполнять построение движений с помощью циркуля и линейки, осуществлять преобразование фигур.

Распознавать по чертежам, осуществлять преобразования фигур с помощью осевой и центральной симметрии, параллельного переноса и поворота.

Применять свойства движения при решении задач.

Применять понятия: осевая и центральная симметрия, параллельный перенос и поворот для решении задач.

«Начальные сведения из стереометрии»

Учащийся получит представления о простейших многогранниках, телах и поверхностях в пространстве; знать формулы для вычисления площадей поверхностей и объёмов тел

«Об аксиомах планиметрии»

Учащийся познакомится с основными аксиомами планиметрии, будет иметь представление об основных этапах развития геометрии.

Повторение курса планиметрии

Применять при решении задач основные соотношения между сторонами и углами прямоугольного и произвольного треугольника.

Применять формулы площади треугольника.

Решать треугольники с помощью теорем синусов и косинусов.

Применять признаки равенства треугольников при решении геометрических задач.

Применять признаки подобия треугольников при решении геометрических задач.

Определять виды четырехугольников и их свойства.

Использовать формулы площадей фигур для нахождения их площади,

выполнять чертеж по условию задачи, решать простейшие задачи по теме «Четырехугольники».

Использовать свойство сторон четырехугольника, описанного около окружности; свойство углов вписанного четырехугольника при решении задач.

Использовать формулы длины окружности и дуги, площади круга и сектора при решении задач.

Решать геометрические задачи, опираясь на свойства касательных к окружности, применяя дополнительные построения, алгебраический и тригонометрический аппарат.

Проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.

Распознавать уравнения окружностей и прямой, уметь их использовать.

Использовать приобретенные знания и умения в практической деятельности для решения практических задач, связанных с нахождением геометрических величин.

Название раздела

Краткое содержание

Количество часов

Повторение курса 8 класса

Свойства треугольников и четырёхугольников (теорема Пифагора, свойство средней линии, свойства и признаки параллелограмма, ромба, прямоугольника, свойства равнобедренного треугольника). Площадь треугольников, четырехугольников. Вписанные и центральные углы.

2

«Векторы»

Определение вектора, начало, конец, нулевой вектор, длина вектора, коллинеарные, сонаправленные, противоположно направленные, равные векторы. обозначение и изображение векторов. Откладывание вектора от данной точки. Сложение и вычитание векторов. Законы сложения, определение суммы, правило треугольника, правило параллелограмма. Построение вектора, равного сумме двух векторов, используя правила треугольника, параллелограмма, многоугольника. Понятие разности двух векторов, противоположных векторов. Определение умножения вектора на число, свойства. Применение векторов к решению задач. Теоремы о средней линии трапеции и алгоритм решения задач с применением этой теоремы.

8

«Метод координат»

Лемма о коллинеарных векторах. Теорема о разложении вектора по двум данным неколлинеарным векторам. Понятие координат вектора, координат суммы и разности векторов, произведения вектора на число. Формулы координат вектора через координаты его конца и начала, координат середины отрезка, длины вектора и расстояния между двумя точками. Уравнение окружности и прямой. Изображение окружности и прямой, заданных уравнениями. Простейшие задачи в координатах. Теорема о скалярном произведении двух векторов и её следствия.

10

«Соотношения между сторонами и углами треугольника. Скалярное

произведение векторов»

Определение синуса, косинуса и тангенса углов от 0º до 180º, формулы для вычисления координат точки, основное тригонометрическое тождество. Формула основного тригонометрического тождества, простейшие формулы приведения. Формула площади треугольника. Теоремы синусов и косинусов. Методы проведения измерительных работ.

12

«Длина окружности и площадь круга»

Определение правильного многоугольника, формула для вычисления угла правильного п - угольника. Теоремы об окружностях: описанной около правильного многоугольника и вписанной в правильный многоугольник. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Формулы длины окружности и длины дуги окружности. Формулы площади круга и кругового сектора. История числа Квадратура круга. Удвоение куба. Построение правильных многоугольников.

11

«Движения»

Понятие отображения плоскости на себя и движения. Свойства движений, осевой и центральной симметрии. Понятие параллельного переноса. Основные этапы доказательства, что параллельный перенос есть движение. Понятие поворота. Доказательство того, что поворот есть движение. Комбинации движений на плоскости и их свойства.

8

«Начальные сведения из стереометрии»

Многогранник и его элементы. Названия многогранников с разным положением и количеством граней. Первичные представления о пирамиде, параллелепипеде, призме, сфере, шаре, цилиндре, конусе, их элементах и простейших свойствах. Представление об объеме и его свойствах. Измерение объема. Единицы измерения объемов. Роль российских ученых в развитии математики: Л. Эйлер. Н.И. Лобачевский, П.Л.Чебышев, С. Ковалевская, А.Н. Колмогоров. Математика в развитии России: Петр I, школа математических и навигацких наук, развитие российского флота, А.Н. Крылов. Космическая программа и М.В. Келдыш.

8

«Об аксиомах планиметрии»

Ознакомление с системой аксиом, положенных в основу изучения курса геометрии. Представление об основных этапах развития геометрии.

2

Повторение курса планиметрии

Начальные геометрические сведения. Параллельные прямые. Окружность. Треугольники. Четырехугольники. Многоугольники. Векторы. Метод координат. Движение.

7

Итого

68

№

п/п

Тема урока

Кол-во

часов

Дата

проведения

Основные виды учебной деятельности

план

факт

1

2

3

4

5

6

Повторение курса геометрии 8 класса – 2 часа

1

Повторение. Свойства четырехугольников.

2

Формулировать определения и иллюстрировать понятия параллелограмма, прямоугольника, ромба, квадрата, трапеции. Формулировать свойства треугольников и четырёхугольников (теорема Пифагора, свойство средней линии, свойства и признаки параллелограмма, ромба, прямоугольника, свойства равнобедренного треугольника) и использовать эти свойства при решении задач. Применять формулы для вычисления площадей треугольников, четырехугольников.

2

Повторение. Свойства треугольников. Теорема Пифагора. Центральные и вписанные углы.

Векторы – 8 часов

3

Понятие вектора. Равенство векторов. Использование векторов в физике.

1

Формулировать определения и иллюстрировать понятия вектора, его длины, коллинеарных и равных векторов; откладывать вектор, равный данному. Строить сумму двух векторов, используя правило треугольника и параллелограмма; строить сумму нескольких векторов, используя правило многоугольника. Строить разность векторов. Формулировать свойства умножения вектора на число.

4

Откладывание вектора от данной точки. Сумма двух векторов. Законы сложения векторов. Правило треугольника и правило параллелограмма.

3

5

Сумма нескольких векторов.

6

Вычитание векторов

7

Умножение вектора на число.

3

8

Умножение вектора на число. Применение векторов в решении задач

9

Средняя линия трапеции.

10

Контрольная работа №1 по теме «Векторы»

1

Метод координат – 10 часов

11

Разложение вектора на составляющие по двум неколлинеарным векторам

2

Объяснять и иллюстрировать понятия прямоугольной системы координат, координат точки и координат вектора. Производить действия над векторами с заданными координатами; уметь определять координаты середины отрезка, вычислять длину вектора, расстояние между точками; формулировать определение скалярного определения векторов. Определять угол между векторами, заданными координатами. Интерпретировать параметры в уравнениях прямой, окружности и строить прямые и окружности, заданные уравнениями.

12

Координаты вектора

13

Действия над векторами . Умножение вектора на число

3

14

Простейшие задачи в координатах. Координаты вектора. Расстояние между точками.

15

Простейшие задачи в координатах. Координаты середины отрезка.

16

Уравнение линии на плоскости.

4

17

Уравнение прямой. Уравнение окружности

18

Решение задач по теме «Уравнение прямой. Уравнение окружности»

19

Применение векторов и координат для решения простейших геометрических задач

20

Контрольная работа №2 по теме «Метод координат»

1

Соотношения между сторонами и углами треугольника. Скалярное произведение векторов – 12 часов

21

Анализ контрольной работы.

Синус, косинус и тангенс угла. Основное тригонометрическое тождество.

5

Формулировать и иллюстрировать определения синуса, косинуса и тангенса углов от 0 до 180°; применять для решения задач основное тригонометрическое тождество и формулы приведения; формулировать теоремы синусов и косинусов, применять их при решении треугольников; объяснять, как используются тригонометрические формулы в измерительных работах на местности.

22

Формулы приведения. Формулы для вычисления координат точки.

23

Теорема о площади треугольника.

24

Теорема синусов.

25

Теорема косинусов

26

Соотношения между углами и сторонами треугольника

5

27

Способы решения треугольников

28

Решение треугольников. Измерительные работы

29

Угол между векторами. Скалярное произведение векторов.

30

Скалярное произведение векторов в координатах и его свойства.

31

Решение задач по теме «Соотношения между сторонами и углами треугольника»

1

32

Контрольная работа №3

по теме «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов»

Длина окружности и площадь круга – 11 часов

33

Анализ контрольной работы. Правильные многоугольники

5

Формулировать определение правильного многоугольника; формулировать теоремы об окружностях, описанной около правильного многоугольника и вписанной в него; знать и использовать формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности; строить правильные многоугольники, в том числе, в виртуальных геометрических конструкторах; объяснять понятия длины окружности и площади круга; знать формулы для вычисления длины окружности и длины дуги, площади круга и площади кругового сектора; применять эти формулы при решении задач.

34

Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник

35

Формулы для вычисления площади правильного многоугольника, его стороны, радиуса вписанной окружности

36

Решение задач на вычисления площади правильного многоугольника, его стороны, радиуса вписанной окружности

37

Решение задач по теме «Правильный многоугольник»

38

Длина окружности

3

39

Решение задач на вычисление длины окружности

40

Площадь круга и кругового сектора. История числа

41

Решение задач на вычисление площади круга и кругового сектора. Квадратура круга. Удвоение куба.

2

42

Построение правильных многоугольников.

43

Контрольная работа №4 по теме

«Длина окружность и площадь круга»

1

Движения – 8 часов

44

Анализ контрольной работы.

Отображение плоскости на себя. Понятие движения .

3

Объяснять, что такое отображение плоскости на себя и в каком случае оно называется движением плоскости. Объяснять, что такое осевая симметрия, центральная симметрия, параллельный перенос и поворот; обосновывать, что эти отображения плоскости на себя являются движениями; объяснять, какова связь между движениями и наложениями. Иллюстрировать основные виды движений, в том числе с помощью компьютерных программ.

45

Свойства движения

46

Осевая и центральная симметрия

47

Параллельный перенос

2

48

Поворот

49

Решение задач по теме «Параллельный перенос. Поворот»

2

50

Решение задач по теме «Движение»

51

Контрольная работа №5 по теме «Движение»

1

Начальные сведения из стереометрии– 8часов

52

Предмет стереометрии. Многогранник и его элементы. Названия многогранников с разным положением и количеством граней.

1

Наглядные представления о пространственных телах: кубе, параллелепипеде, призме, пирамиде, шаре, сфере, конусе, цилиндре. Примеры сечений. Примеры разверток. Определение многогранника. Правильные многогранники. Объем тела. Формулы объема прямоугольного параллелепипеда, куба, пирамиды, шара, цилиндра и конуса.

53

Первичные представления о пирамиде, параллелепипеде, призме, цилиндре. Элементы и простейшие свойства этих фигур.

1

54

Первичные представления о конусе, сфере, шаре. Элементы и простейшие свойства этих фигур.

1

55

Представление об объёме и его свойствах. Измерение объема. Единицы измерения объема.

1

56

Решение простейших задач на вычисление объемов многогранников

1

57

Защита проектных работ по теме «Роль российских ученых в развитии математики: Л.Эйлер, Н.И.Лобачевский, П.Л.Чебышев, С.Ковалевская, А.Н. Колмогоров». «Математика в развитии России: Петр I, школа математических и навигацких наук. Развитие российского флота, А. Н. Крылов ». «Космическая программа и М. В. Келдыш»

3

58

59

«Об аксиомах планиметрии» – 2 часа

60

Об аксиомах планиметрии

2

61

Основные этапы развития геометрии

Итоговое повторение курса геометрии 9 класса – 7 часов

62

Повторение темы «Треугольники», «Окружность»

1

Повторить основные отношения между сторонами и углами треугольника, формулы площади треугольника

63

Повторение темы «Четырехугольники. Многоугольники»

1

Повторить основные формулы дины окружности и дуги, площади круга и кругового сектора.

64

Повторение темы «Векторы. Метод координат», «Параллельные прямые»

1

Повторить основные виды четырехугольников, их свойства, формулы площадей.

65

Итоговая контрольная работа по геометрии

1

Повторить основные операции над векторами, вычисление длины и координаты вектора, угла между векторами

66

Анализ контрольной работы.

Обобщающий урок по все темам геометрии 9 класса

1

Повторить основные свойства и признаки параллельных прямых.

67

Подготовка к ОГЭ. Решение заданий КИМ ОГЭ

1

68

Подготовка к ОГЭ. Решение заданий КИМ ОГЭ

1

Класс

Название раздела, темы

Дата проведения по плану

Причина корректировки

Корректирующие мероприятия

Дата проведения по факту