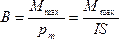Контур с током в магнитном поле. Работа перемещения проводника с током в магнитном поле.
 Закон Ампера. Взаимодействие параллельных токов.
Закон Ампера. Взаимодействие параллельных токов.
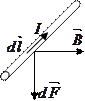
Закон Ампера: сила 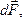 с которой магнитное поле действует на элемент проводника
с которой магнитное поле действует на элемент проводника 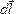 с током
с током 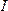 , находящегося в магнитном поле, прямо пропорциональна силе тока
, находящегося в магнитном поле, прямо пропорциональна силе тока 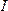 и векторному произведению элемента длины
и векторному произведению элемента длины 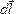 на магнитную индукцию
на магнитную индукцию 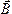 :
:
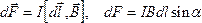
Если  ,
, 
 Направление силы Ампера определяется правилом левой руки.
Направление силы Ампера определяется правилом левой руки.
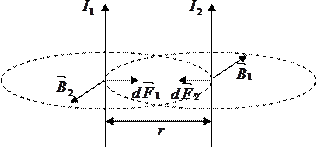
Закон Ампера применяется для определения силы взаимодействия двух бесконечных прямолинейных параллельных проводников с токами 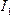 и
и 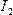 , расположенных в вакууме на расстоянии
, расположенных в вакууме на расстоянии  . Каждый из проводников создает магнитное поле, которое по закону Ампера действует на другой проводник.
. Каждый из проводников создает магнитное поле, которое по закону Ампера действует на другой проводник.
Определим силу, с которой магнитное поле тока 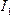 , действует на элемент
, действует на элемент 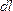 второго проводника с током
второго проводника с током 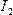
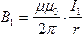
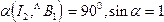
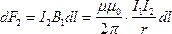
Рассуждая аналогично, можно показать, что
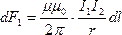 .
.
По III закону Ньютона 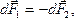 т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой
т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой
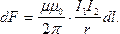
Аналогично можно доказать, что токи противоположного направления отталкиваются с такой же силой.
Если I1 = I2 = 1A, r=1м, l=1м, F1 = F2 = 2×10-7H ® определение 1A.
Контур с током в магнитном поле. Работа перемещения проводника с током в магнитном поле.
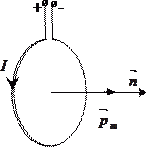 Магнитный момент контура с током - это векторная физическая величина численно равная произведению силы тока на площадь контура.
Магнитный момент контура с током - это векторная физическая величина численно равная произведению силы тока на площадь контура.
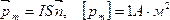
1 А×м2 - это магнитный момент контура с током силой 1А, площадь которого равна 1м2.
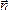 - единичный вектор внешней нормали к поверхности S, ограниченной контуром с током.
- единичный вектор внешней нормали к поверхности S, ограниченной контуром с током.
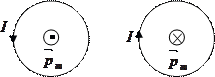 Внешней (положительной) называется нормаль, которая связана с направлением тока в контуре правилом правого винта. Таким образом, направление
Внешней (положительной) называется нормаль, которая связана с направлением тока в контуре правилом правого винта. Таким образом, направление 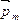 определяется правилом правого винта: если рукоятку винта вращать по току в контуре, поступательное движение винта совпадет с направлением
определяется правилом правого винта: если рукоятку винта вращать по току в контуре, поступательное движение винта совпадет с направлением 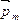 .
.
Поместим в однородное магнитное поле с индукцией 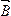 рамку с током
рамку с током 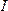 так, чтобы плоскость рамки была параллельна магнитным силовым линиям. При этом на стороны рамки, перпендикулярные силовым линиям (
так, чтобы плоскость рамки была параллельна магнитным силовым линиям. При этом на стороны рамки, перпендикулярные силовым линиям ( 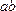 и
и 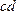 ) будут действовать силы
) будут действовать силы 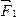 и
и 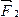 , создающие вращающий момент сил относительно закрепленной оси вращения 00¢.
, создающие вращающий момент сил относительно закрепленной оси вращения 00¢.
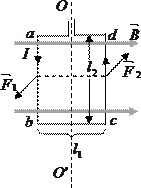
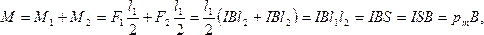
где 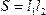 - площадь рамки,
- площадь рамки,
pm - магнитный момент рамки с током.
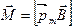
Вращающий момент стремится привести контур в положение устойчивого равновесия, при котором векторы 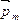 и
и 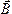 сонаправлены, т.е. ориентированы параллельно друг другу. При этом М=0, силы
сонаправлены, т.е. ориентированы параллельно друг другу. При этом М=0, силы 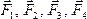 действуют в одной плоскости, они лишь деформируют рамку (растягивают).
действуют в одной плоскости, они лишь деформируют рамку (растягивают).
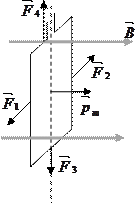 Следовательно, действие однородного магнитного поля на рамку (контур) с током сводится к повороту
Следовательно, действие однородного магнитного поля на рамку (контур) с током сводится к повороту 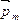 в направлении, параллельном
в направлении, параллельном 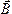 (
( 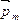 сонаправлено
сонаправлено 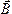 ).
).
Из предыдущей формулы может быть дано определение 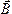 : модуль вектора магнитной индукции в данной точке магнитного поля равен максимальному вращающему моменту сил, действующих на рамку с током, обладающую единичным магнитным моментом:
: модуль вектора магнитной индукции в данной точке магнитного поля равен максимальному вращающему моменту сил, действующих на рамку с током, обладающую единичным магнитным моментом:
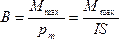
Если поле неоднородно, под действием силы незакрепленный контур с током втягивается в область более сильного магнитного поля.
На проводник с током в магнитном поле действует сила Ампера. Если проводник не закреплен (например, одна сторона контура изготовлена в виде подвижной перемычки), то под действием силы Ампера он будет перемещаться в магнитном поле, т.е. сила Ампера совершает работу по перемещению проводника с током в магнитном поле. Для ее определения рассмотрим проводник длиной 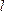 с током I, который может свободно перемещаться в однородном магнитном поле с индукцией
с током I, который может свободно перемещаться в однородном магнитном поле с индукцией 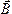 .
.

Под действием этой силы проводник переместится параллельно самому себе на dx из положения 1 в положение 2 . Работа, совершенная при этом:
,
где dS=ldx - площадь, пересекаемая проводником при его движении;
dIm = BdS - магнитный поток, пронизывающий эту площадь.
Полученная формула справедлива и для произвольного направления
вектора 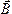 , т.к.
, т.к. 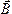 можно разложить на нормальную Bn и тангенциальную (по отношению к плоскости контура) составляющие.
можно разложить на нормальную Bn и тангенциальную (по отношению к плоскости контура) составляющие.
Поскольку Bt в создании F не участвует, то
dA = I Bnldx = I BndS = I dФm
Если 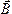 =const, A = I Фm,
=const, A = I Фm,
т.е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
Работа совершается не за счет энергии внешнего магнитного поля, а за счет источника, поддерживающего неизменным ток в контуре, или в перемещаемом проводнике.
Вычислим работу по перемещению замкнутого контура с током в магнитном поле. Для упрощения вычислений рассмотрим контур прямоугольной формы, плоскость которого перпендикулярна 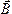 и с которым сцеплен магнитный поток Фm1. Поскольку магнитное поле в общем случае может быть неоднородным, при перемещении контура 1234 в плоскости чертежа в новое положение 1¢ 2¢ 3¢ 4¢ с ним будет сцеплен магнитный поток Фm2. Магнитный поток сквозь площадку 432¢1¢ обозначим Фm.
и с которым сцеплен магнитный поток Фm1. Поскольку магнитное поле в общем случае может быть неоднородным, при перемещении контура 1234 в плоскости чертежа в новое положение 1¢ 2¢ 3¢ 4¢ с ним будет сцеплен магнитный поток Фm2. Магнитный поток сквозь площадку 432¢1¢ обозначим Фm.
Полная работа, совершаемая при перемещении контура, равна алгебраической сумме работ, совершаемых при перемещении 4-х сторон:
A = A12 +A23 +A34 +A41
A23 = A41 = 0 (т.к. F23 и F41 перпендикулярны перемещению)
Т.к. сила  составляет с вектором перемещения 1800, A12
составляет с вектором перемещения 1800, A12
A12 = - I(Фm1 + Фm)
Сила  сонаправлена с вектором перемещения, A340
сонаправлена с вектором перемещения, A340
A34 = I(Фm + Фm2)
А = I(-Фm1-Фm+Фm +Фm2)= I(Фm2-Фm1) = IDФm, (1)
где DФ - изменение магнитного потока через площадку, ограниченную замкнутым контуром.
Работа, совершаемая силами Ампера при перемещении замкнутого контура с током в магнитном поле, равна произведению силы тока на изменение магнитного потока, сцепленного с контуром.
Соотношение (1), полученное для простейшего случая, справедливо для контура любой конфигурации в произвольном магнитном поле при любых его перемещениях (вращении, сминании и т.п.).
В частности, при повороте контура в однородном магнитном поле из положения 1, при котором  в положение 2, при котором
в положение 2, при котором  над контуром совершается работа:
над контуром совершается работа:
Если контур неподвижен, а изменяется значение или направление 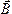 , работа рассчитывается также по формуле (1).
, работа рассчитывается также по формуле (1).
Сила Лоренца. Движение заряженных частиц в магнитном поле.
Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q ,движущийся в магнитном поле 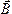 со скоростью
со скоростью  , называется силой Лоренца.
, называется силой Лоренца.
 - установлено опытным путем
- установлено опытным путем
Направление силы Лоренца определяется для положительных зарядов правилом левой руки (т.к. направление 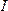 и
и  для
для  совпадают): если ладонь левой руки расположить так, чтобы вектор
совпадают): если ладонь левой руки расположить так, чтобы вектор 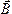 входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца.
входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца.
Для отрицательных зарядов берется противоположное направление.
Сила Лоренца всегда направлена перпендикулярно скорости заряда  и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля действует и электрическое поле напряженностью  , то результирующая сила
, то результирующая сила
 - формула Лоренца.
- формула Лоренца.
1 . Движение заряженной частицы вдоль силовой линии,
. Движение заряженной частицы вдоль силовой линии,  .
.
 ,
,
магнитное поле не действует на частицу.
Заряженная частица движется по инерции равномерно прямолинейно.
2. Движение заряженной частицы перпендикулярно силовым линиям,  .
.
Пусть в однородное магнитное поле с индукцией 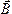 влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью
влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью  .
.
В каждой точке поля на частицу действует  . Т.к.
. Т.к.  , то
, то  . Ускорение
. Ускорение  изменяет только направление скорости,
изменяет только направление скорости,  , значит,
, значит,  . В этих условиях тело (заряженная частица) движется равномерно по окружности.
. В этих условиях тело (заряженная частица) движется равномерно по окружности.
Согласно II закону Ньютона:

(1)
Т.к. все величины, входящие в (1), постоянны, радиус кривизны R будет оставаться постоянным. Постоянный радиус кривизны имеет только окружность. Следовательно, движение заряда в плоскости, перпендикулярной магнитному полю, будет происходить по окружности. Чем больше 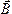 , тем меньше R. При
, тем меньше R. При  , т.е. заряд движется по прямой.
, т.е. заряд движется по прямой.
Важным результатом для приложения является тот факт, что период обращения заряда в однородном магнитном поле не зависит от его скорости.
 если . (2)
если . (2)
Частицы, имеющие бóльшую скорость, движутся по окружности бóльшего радиуса, однако время одного полного оборота будет таким же, что и для более медленных частиц, движущихся по окружности меньшего радиуса. Данный результат положен в основу действия циклических ускорителей элементарных частиц.
3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции.
Вектор скорости можно разложить на 2 составляющие:

В направлении 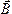 сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с
сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с  . В направлении, перпендикулярном
. В направлении, перпендикулярном 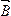 , он движется по окружности со скоростью
, он движется по окружности со скоростью  Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна
Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна 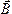 .
.
Радиус витка с учетом (1):
 (3)
(3)
Ш аг винтовой линии (расстояние между соседними витками)
с учетом (2):
.
Если движение происходит в неоднородном магнитном поле, индукция которого возрастает в направлении движения частицы, то R уменьшается с ростом В согласно (3). На этом основана фокусировка пучка заряженных частиц в магнитном поле. Таким образом, с помощью неоднородного магнитного поля можно управлять пучками заряженных частиц, собирать их или рассеивать подобно тому, как управляют поведением пучков световых лучей с помощью оптических линз.
Рассмотренный принцип положен в основу действия электронных микроскопов.
Ускорители заряженных частиц.
Свойство независимости периода от скорости обращения используют для того, чтобы превратить траекторию ускоряемой частицы в спираль и уменьшить размеры ускорителя. Такой принцип положен в основу работы циклотрона - родоначальника целого семейства ускорителей с магнитным полем: синхротрона, синхрофазотрона и т.д.
Ускорительная камера циклотрона представляет собой вакуумную цилиндрическую коробку, помещенную между полюсами сильного электромагнита. Камера состоит из двух металлических половинок - дуантов, между которыми создается с помощью генератора переменное электрическое напряжение с амплитудой порядка  (поле только в зазоре). Частицы вводятся внутрь камера с помощью специального впускного устройства (А).
(поле только в зазоре). Частицы вводятся внутрь камера с помощью специального впускного устройства (А).

При каждом пересечении зазора частица приобретает энергию DE1 = qU. За N оборотов DE = qUN, DEmax~107эВ.
Большая энергия в циклотроне не может быть достигнута: как следует из теории относительности: m = f(V), а при росте массы уменьшается частота обращения.
В синхроциклотронах (фазотронах) медленно уменьшается частота подаваемого напряжения.
Фазотрон - изменяется n.
В синхротронах меняется индукция магнитного поля 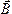 .
.
Синхротрон - изменяется 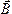
В синхрофазотронах - изменяется n и B.
DE~109 - 1010 эВ.
Ускорители заряженных частиц - устройства, в которых создаются и управляются пучки высокоэнергетических заряженных частиц под действием электрических и магнитных полей.
Принцип автофазировки предложены советским физиком Векслером (1944 г.) и американским Мак-Милланом (1945 г.).
Магнитогидродинамический (МГД) генератор - установка для непосредственного преобразования тепловой энергии в электрическую (создан в 50-х годах).
Это источник тока, принцип действия которого основан на действии магнитного поля на заряженные частицы плазмы электролитов и жидких металлов. Плазма представляет собой поток раскаленного газа, все молекулы которого ионизированы высокой температурой (~2000K).
Поток плазмы, проходя через расширяющееся сопло, ускоряется до 2000-2500 м/с и попадает в сильное магнитное поле, разделяющее положительные и отрицательные заряды, отбрасывая их на электроды. При этом во внешней цепи возникает электрический ток.
 т.к. Tпл Твн.среды, h - велико.
т.к. Tпл Твн.среды, h - велико.
Применение:
1) в ускорителях;
2) в НГД - генераторах;
3) датчиках Холла;
4) для осуществления управляемых термоядерных реакций;
5) при регистрации и исследовании заряженных частиц;
6) в магнетронах.


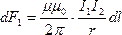 .
.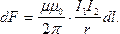

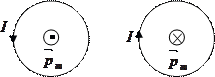

 Следовательно, действие однородного магнитного поля на рамку (контур) с током сводится к повороту
Следовательно, действие однородного магнитного поля на рамку (контур) с током сводится к повороту