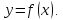Конспект урока алгебры по теме «Применение производной для исследования функций на монотонность и экстремумы». 10 класс
Соколова Ольга Николаевна, учитель математики
Учебник: Мордкович А.Г., Семёнов П.В. «Математика: алгебра и начала математического анализа, геометрия 10-11 классы». В двух частях.
Тип урока: урок-исследование.
Цели урока:
Образовательные:
- вспомнить основные понятия по теме производной, по исследованию функций;
- научиться применять производную для исследования характера монотонности функции на промежутках: по знаку производной определять, убывает или возрастает функция; изучить понятия точек экстремума, достаточные условия экстремума, научиться применять производную для нахождения точек экстремума; научиться решать задачи на нахождение промежутков монотонности и точек экстремума функции; изучить алгоритм исследования непрерывной функции на монотонность и экстремумы.
Развивающие:
- продолжать содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;
- продолжать формировать и развивать общеучебные умения и навыки: исследование, обобщение, поиск способов решения;
Воспитательные:
- вырабатывать умения рассуждать, высказывать предположения по теме, отвечать на вопросы в устной форме, задавать вопросы;
- вырабатывать умения строить правильные речевые высказывания с математическими терминами, устанавливать причинно-следственные связи, грамотно вести дискуссию;
- способствовать формированию активности, максимальной работоспособности, умению отстаивать свою точку зрения, принимать другую, умению сотрудничать с одноклассниками, учителем.
Структура урока:
Ι.Организационный момент.
ΙΙ. Мотивация. Восприятие и осознание проблемы.
ΙΙΙ. Формулировка гипотезы исходя из данных условий. Поиск решений.
ΙV. Доказательство и проверка гипотезы.
V. Нахождение результата.
VΙ. Рефлексия. Запись домашнего задания.
Ход урока
Ι.Организационный момент. Продолжительность: 1-2 минуты.
Задачи этапа: обеспечить внешнюю обстановку для работы на уроке, психологически настроить учащихся к общению.
Содержание этапа:
1. Приветствие.
Учитель: Здравствуйте, садитесь! Запишите сегодняшнее число и тему урока: “Применение производной для исследования функций на монотонность и экстремумы”. Задания по данной теме встречаются в вариантах ЕГЭ. Слайд 1.
2. Проверка готовности учащихся к уроку.
Учитель: Ребята, кто сегодня отсутствует? Все готовы к уроку? Итак, внимание. Начинаем!
3. Озвучивание целей урока и плана его проведения.
Учитель: Я думаю, вам будет интересно сегодня на уроке, так как урок нестандартный, а именно мы проведём урок-исследование. Слайд 2.
Цель нашего урока – не только изучить тему, но научиться исследовать: учиться задавать вопросы, выдвигать предположения , отвечать на вопросы, осуществлять поиск информации, устанавливать причинно-следствееные связи, делать выводы.
В начале урока мы «соберём корзину идей», куда поместим все-все мысли, идеи, слова, которые возникают у Вас при знакомстве с названием темы.
После чего составим круг вопросов, на которые нам предстоит ответить, чтобы понять тему. Исходя из этого, сделаем предположение.
Затем осуществим поиск решений, проверим наше предположение, ответим на все вопросы. Далее обсудим полученные результаты работы на уроке. После чего вы получите домашнее задание.
Согласны с таким планом работы? Хорошо! Итак, приступаем.
ΙΙ. Мотивация. Восприятие и осознание проблемы. Продолжительность: 3-4 минуты.
Задачи этапа: создание условий для возникновения у ученика вопроса или проблемы, формирование круга вопросов изучения и пути поиска решения.
Содержание этапа:
1. Фронтальная устная форма работы. Используется приём «Корзина идей». На доске нарисована мелом корзина, внутри неё учитель записывает слова, мысли, фразы, которые возникают у учащихся при прочтении названия темы.
Учитель: Ребята, давайте соберём «корзину идей». Слайд 3. Для этого ещё раз посмотрите на название темы нашего урока и попробуйте предположить , о чём эта тема, с какими математическими понятиями, элементами она может быть связана. Все слова, фразы или мысли, которые у вас возникли, запишем в нашу корзину.
Учитель опрашивает каждого учащегося, ответы заносит на доску в корзину, корректирует ответы, направляет в нужное русло мысли учащихся, чтобы приблизить их к пониманию смысла темы урока.
Предполагаемые ответы учащихся на доске: Убывание, возрастание, промежутки, график, точки касания, критические, стационарные точки, нахождение производной, касательная, угловой коэффициент, знак производной, существование производной, связь между производной и промежутками монотонности и т.д.
2. Учитель на основе выше сказанных слов подводит учащихся к проблеме.
Учитель: Таким образом, ребята, на какой вопрос мы должны ответить при изучении темы?
Предполагаемый ответ учащихся: Как связана производная функции с монотонностью и эктремумами функции? ( Можно ли с помощью производной найти промежутки возрастания и убывания функции и экстремумы функции?) Слайд 4.
ΙΙΙ. Формулировка гипотезы исходя из данных условий. Поиск решений. Продолжительность: 2-3 минуты.
Задачи этапа: создание условий для поиска решений проблемы учащимися, выдвижения ими предварительных гипотез, установления причинно-следственных связей.
Содержание этапа:
Учитель: Итак, главный вопрос темы сформулирован. Ребята, попробуйте ответить на него на основе вышесказанного, т.е. сделать предположение.
Учащиеся высказывают свои мысли, учитель корректирует, поправляет. Затем учащиеся с помощью учителя приходят к одному предоположению и записывают гипотезу в тетради: «По знаку производной можно установить характер монотонности функции на промежутке и найти точки экстремума функции». Слайд 5
Учитель: Итак, теперь нам предстоит доказать или опровергнуть данную гипотезу.
ΙV. Доказательство и проверка гипотезы. Продолжительность: 20-25 минут.
Задачи этапа: создание условий для возникновения необходимости поиска новых способов объяснения или действий, для потребности в новых знваниях, вырабатывания варианта решения данной проблемы.
Содержание этапа:
1. Учитель: Вспомните, какая существует связь между производной в некоторой точке и касательной, проведенной в этой же точке.
Предполагаемый ответ: если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то угловой коэффициент касательной равен производной в данной точке.
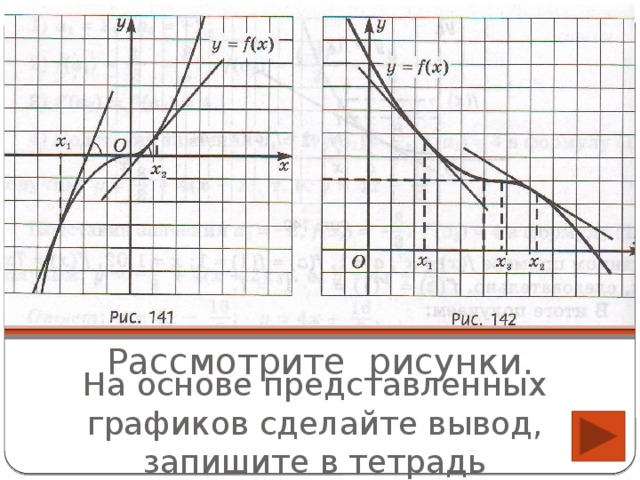
Учитель: Рассмотрите рисунки 141, 142 в учебнике. Слайд 6.
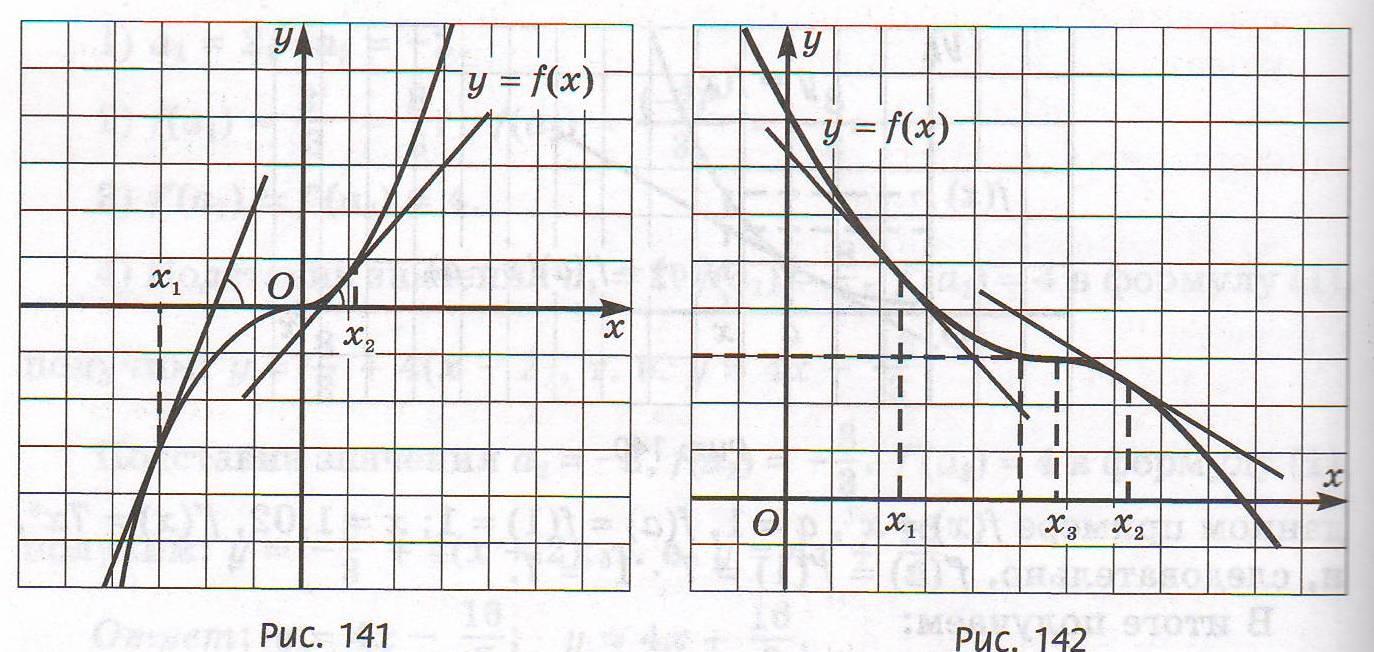
На основе представленных графиков сделайте вывод.
Предполагаемый ответ: если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна; если функция убывает на промежутке и имеет на нём производную, то производная неположительна. Учащиеся делают записи в тетради. Слайд 7 (Дм 13).
Учитель: А как вы думаете, обратные утверждения будут верны? Сформулируйте их и сделайте вывод по всему сказанному. Учитель помогает сформулировать корректное утверждение и сделать правильный вывод. Предполагаемый ответ: по знаку производной можно установить характер монотонности функции на промежутке.
После этого учащиеся записывают теремы 1,2 параграфа 30 учебника:
Теорема 1. Если во всех точках открытого промежутка X выполняется неравенство 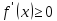 , то функция
, то функция 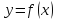 возрастает на промежутке X.
возрастает на промежутке X.
Теорема 2. Если во всех точках открытого промежутка X выполняется неравенство 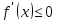 , то функция
, то функция 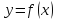 убывает на промежутке X.
убывает на промежутке X.
Учитель: Чтобы убедиться в правильности наших рассуждений, рассмотрим задачу 1 с конретной функцией.
Учащиеся с помощью учителя решают задачу на доске. Слайд 8.
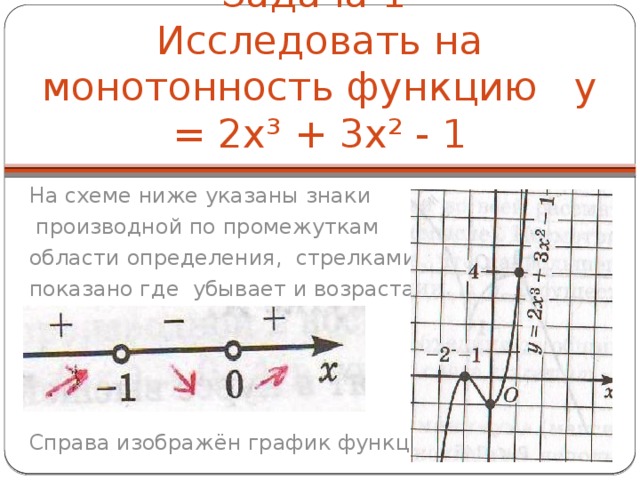
Задача 1. Исследовать на монотонность функцию 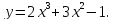
Решение: Исследовать функцию на монотонность - это значит выяснить, на каких промежутках области определения функция возрастает, а на каких – убывает. Согласно сделанными нами выводам, это связано со знаком производной.
Найдём производную данной функции: 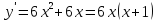 . Найдём знаки производной на промежутках области определения, для этого приравняем к 0:
. Найдём знаки производной на промежутках области определения, для этого приравняем к 0:
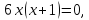 получим стационарные точки
получим стационарные точки 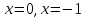 ,
,
изобразим схематически знаки производной, стрелочками возрастание и убывание функций на полученных промежутках: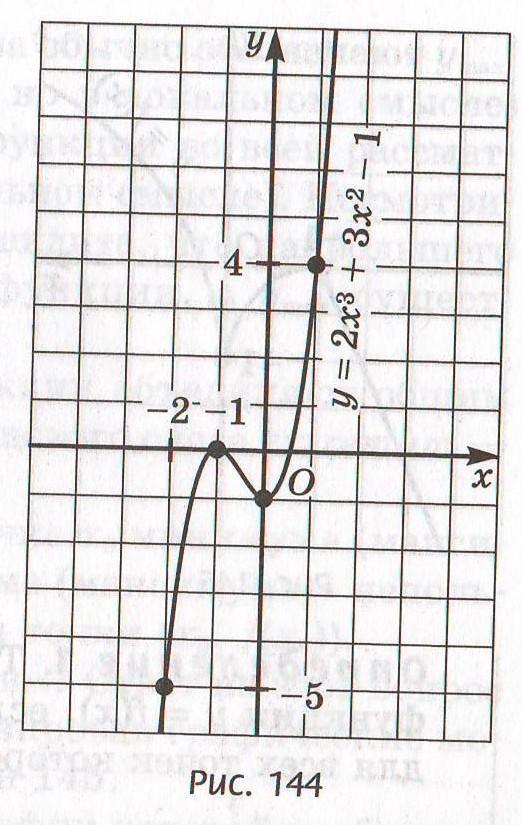
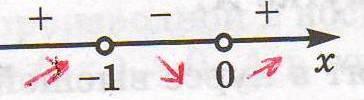
Ответ: функция 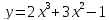 возрастает при
возрастает при 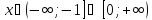 , убывает при
, убывает при 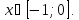
Учитель: в учебнике на рис. 144 построен график данной функции. Убедитесь по рисунку, что всё найдено верно и выполняются все утверждения. Можно сказать, что первая часть гипотезы подтвердилась?
Предполагаемый ответ: да, вывод - по знаку производной можно установить характер монотонности функции на промежутке.
2. Учитель: Итак, первая часть гипотезы выполняется, продолжаем дальше. Осталось проверить, можно ли по знаку производной найти точки экстремума функции. Какое затруднение у Вас возникло?
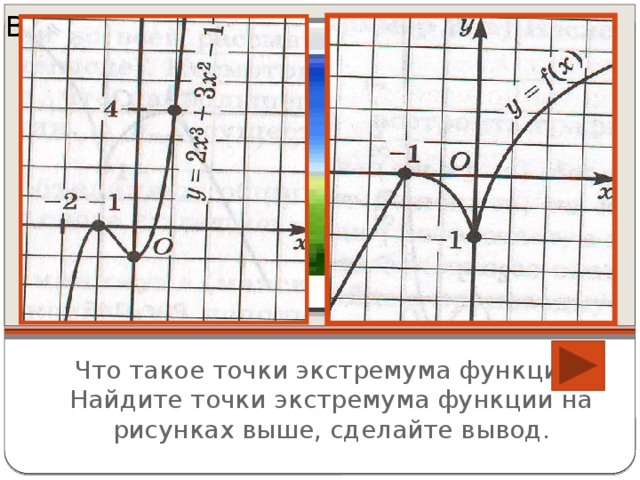
Предполагаемый ответ: неизвестный термин – экстремум. Учитель предлагает узнать значение термина, опираясь на текст пункта 2 параграфа 30 учебника. Учитель поясняет определение по слайду 9 (Дм 14). Далее учитель предлагает найти точки экстремума функции на рис.144, затем на рис.145 в учебнике.

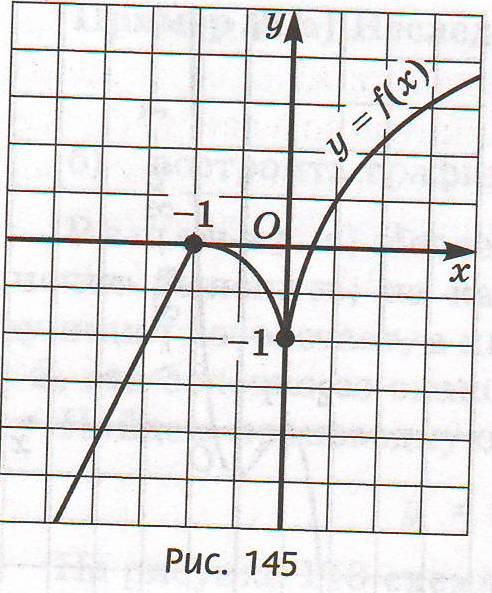
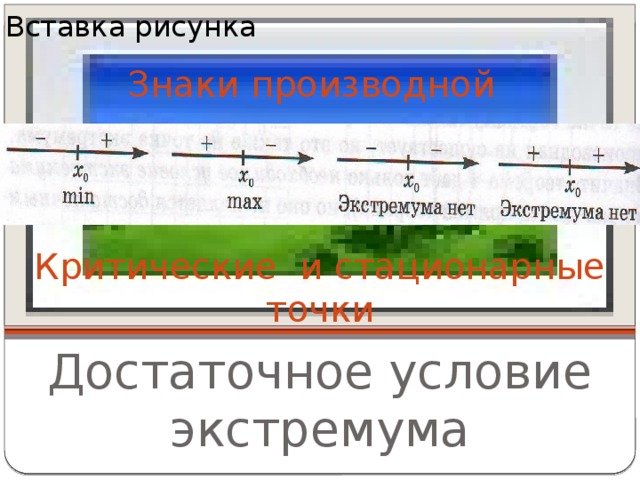
Учитель: на основе представленных рисунков, пользуясь всем выше сказанным, сделайте вывод. Предполагаемый ответ: в точках экстремума производная либо равна нулю (в стационарной точке), либо не существует (в критической точке).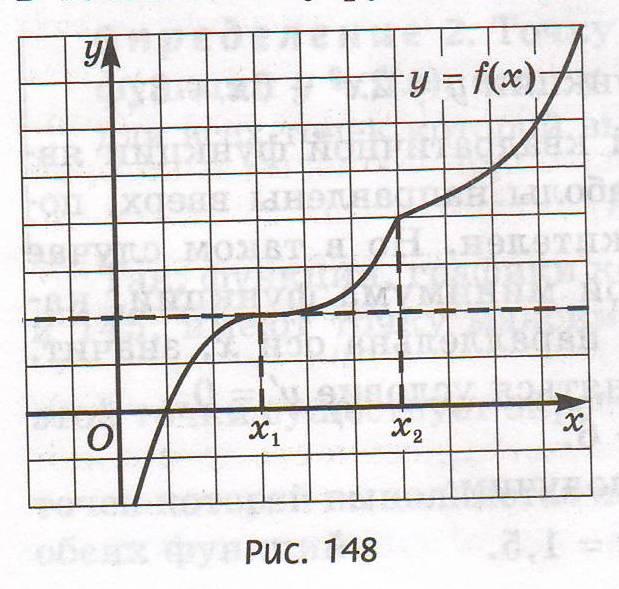
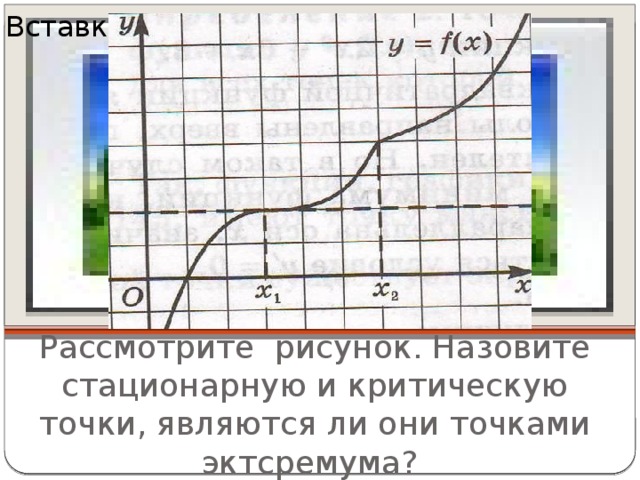
Учитель: А как вы думаете, обратное утверждение верно, т.е. если точка стационарная или критическая, то оня является точкой экстремума? Чтобы ответить на этот вопрос, рассмотрим рис. 148 учебника. Слайд 10. Назовите стационарную и критическую точки, являются ли они точками эктсремума.
Предполагаемый ответ: нет, так как у них нет такой окрестности, в которой выполнялись условия определения для точки эктсремума или на промежутке до этих точек производная положительная, и после тоже положительна.
Учитель: В случае нахождения точек экстремума функции пользуются теоремой, которая называется достаточным условием экстремума, в учебнике теорема 5. Прочитайте эту теорему и изобразите условную схему для знаков производной в тетради (Слайд 11):
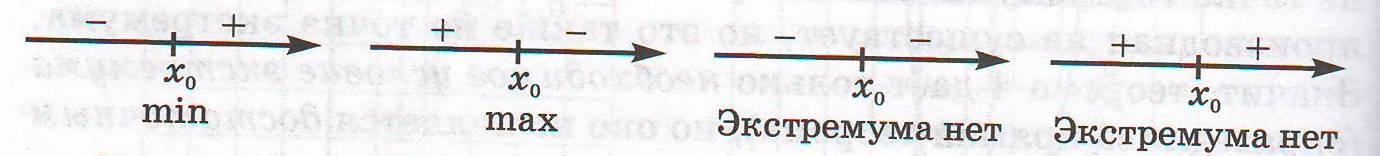
Учитель: Ребята, существует ли связь между производной и точками эктсремума функции? Какая? Сделайте вывод.
Предполагаемый ответ: по знаку производной можно найти точки экстремума. Слайд 12.
Учитель: Чтобы убедиться в правильности наших рассуждений, рассмотрим задачу 2 с конретной функцией. Слайд 13.
Учащиеся с помощью учителя решают задачу.
Задача 2. Найти точки экстремума функции 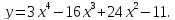
Решение: Сначала найдём производную данной функции:
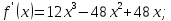
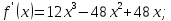
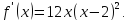
Производная всюду существует, значит критических точек у функции нет. Найдём стационарные точки, т.е. точки, в которых производная равна нулю:
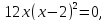 получим
получим 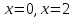 .
.
Изобразим схематически знаки производной по промежуткам области определения:

На промежутки 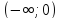 производная отрицательна, на промежутке (0; 2) – положительна, на промежутке (2;
производная отрицательна, на промежутке (0; 2) – положительна, на промежутке (2; 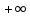 ) – положительна.
) – положительна.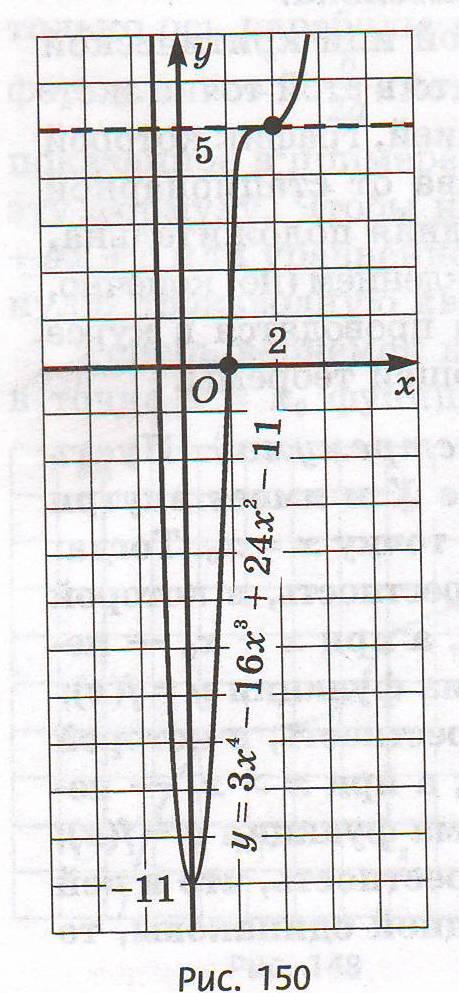
Учитель: Так в какой же точке будет эктсремум функции? Предполагаемый ответ учащихся: на первом промежутке функция убывает, на втором возрастает, на третьем возрастает, значит, 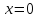 - точка минимума функции, а
- точка минимума функции, а 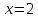 точкой экстремума не является.
точкой экстремума не является.
Ответ: 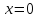 - точка минимума функции
- точка минимума функции 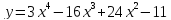 .
.
Учитель: В учебнике на рис. 150 построен график данной функции. Убедитесь по рисунку, что всё найдено верно и выполняются все утверждения. Обратите внимание, что в точке 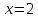 производная равна нулю, но точкой экстремума она не является. Таким образом, можно сказать, что вторая часть гипотезы подтвердилась?
производная равна нулю, но точкой экстремума она не является. Таким образом, можно сказать, что вторая часть гипотезы подтвердилась?
Предполагаемый ответ: да, вывод - по знаку производной можно найти точки экстремума функции.
V. Нахождение результата. Продолжительность: 5-7 минут.
Задачи этапа: создание условий для выработки походящего варианта, формирования учащимися окончательных выводов.
Содержание этапа:
Учитель: Ребята, посмотрите на решение задач 1 и 2. Если сравнить их по шагам между собой, что можно заметить?
Предполагаемый ответ учащихся: решение практически одинаковое, отличие только в заключении задач, при ответе на вопрос задания.
Учитель: Завершая наше исследование, попробуйте выделить этапы решения задач такого типа и выработать алгоритм, записать в тетрадь.
Учащиеся с помощью учителя выделяют шаги, выводят правило, записывают алгоритм в тетрадь, используя текст параграфа 30 учебника на стр.209. Слайд 14.
Алгоритм исследования непрерывной функции 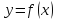 на монотонность и экстремумы
на монотонность и экстремумы
1. Найти производную 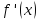 .
.
2. Найти стационарные (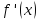 =0) и критические (
=0) и критические (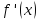 не существует) точки функции
не существует) точки функции 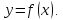
3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4. На основании теорем 1,2 и 5 сделать выводы о монотонности функции и её точках экстремума.
Учитель: Итак, ребята, сегодня вы исследовали важнейшую тему математического анализа, выдвинули гипотезу и её доказали. Предлагаю вам сформулировать окончательный вывод по всей теме.
Предполагаемый ответ учащихся: с помощью знака производной можно исследовать функцию на монотонность и находить точки экстремума.
VΙ. Рефлексия. Запись домашнего задания. Продолжительность: 5-6 минут.
Задачи этапа: создание условий для рефлектирования, синтеза и обобщения понятий и информации.
Содержание этапа:
Учитель: И теперь предлагаю вам составить синквейн к сегоднешней теме. Напомню правила составления синквейна. Слайд 15.
1 строка – одно слово, существительное, отражающее главную идею;
2 строка – два слова, прилагательные, описывающие основную мысль;
3 строка – три слова, глаголы, описывающие действия в рамках темы;
4 строка - фраза из нескольких слов, выражающая отношение к теме;
5 строка – одно слово (ассоциация, синоним к теме, эмоциональное отношение к теме).
Учитель: Откройте дневники, запишите домашнее задание: параграф 30 (учить определения, теоремы, алгоритм), выполнить № 30.8, 30.13(в,г). Слайд 16.
Учитель: Слайд 17. Дорогие ребята! Спасибо вам за работу на уроке. Я благодарю всех, кто принял активное участие в работе. Урок окончен. До свидания!
Список литературы
1. Мордкович А.Г., Семёнов П.В. «Математика: алгебра и начала математического анализа, геометрия 10-11 классы». В двух частях. «Мнемозина», 2014.
2. Бортакивский А.С., Закалюкин В.М., Шапошников В.П. “Экзаменационные задачи и варианты по математике”. М., МАИ-ПРИНТ, 2009.
3. Рурукин А.Н. “Контрольно-измерительные материалы. Алгебра и начала анализа: 10 класс”, М., “ВАКО”, 2011.

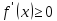 , то функция
, то функция 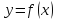 возрастает на промежутке
возрастает на промежутке 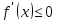 , то функция
, то функция 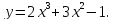
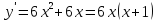 . Найдём знаки производной на промежутках области определения, для этого приравняем к 0:
. Найдём знаки производной на промежутках области определения, для этого приравняем к 0: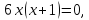 получим стационарные точки
получим стационарные точки 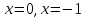 ,
, 

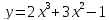 возрастает при
возрастает при 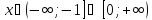 , убывает при
, убывает при 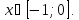


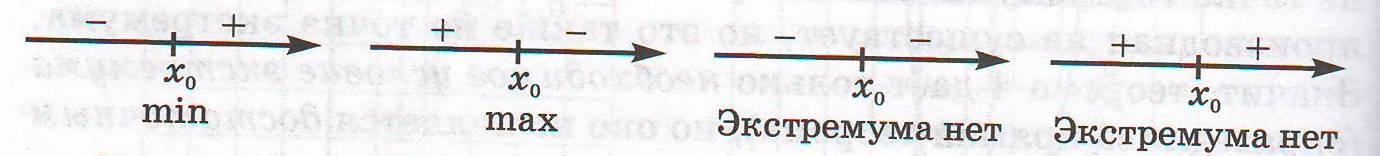
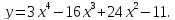
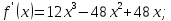
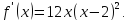
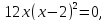 получим
получим 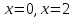 .
.
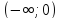 производная отрицательна, на промежутке (0; 2) – положительна, на промежутке (2;
производная отрицательна, на промежутке (0; 2) – положительна, на промежутке (2; 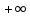 ) – положительна.
) – положительна.
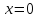 - точка минимума функции, а
- точка минимума функции, а 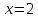 точкой экстремума не является.
точкой экстремума не является.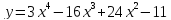 .
.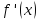 .
.