Рабочая программа по алгебре 8 кл.

Пояснительная записка

Рабочая программа разработана в соответствии с требованиями федерального компонента государственного образовательного стандарта общего образования на основе документов:

• Примерные программы основного общего образования. Математика. – М.: Просвещение, 2011. – (Стандарты второго поколения);

• Фундаментальное ядро содержания общего образования / под ред. В.В.Козлова, А.М.Кондакова. — М.: Просвещение, 2010. – (Стандарты второго поколения);

• Сборник рабочих программ. Алгебра. 7-9 классы / [составитель Т. А. Бурмистрова]. – М. Просвещение, 2012;

• Примерная основная образовательная программа образовательного учреждения. Основная школа / [составитель Е.С.Савинов]. – М.: Просвещение, 2011. – (Стандарты второго поколения);

• Учебный план МКОУ СОШ №12 с. Николина Балка.

• Образовательная программа МКОУ СОШ №12 с. Николина Балка.

• При составлении рабочей программы учтены рекомендации авторского коллектива УМК под редакцией Г.В.Дорофеева, а также основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.

Рабочая программа по алгебре для 8 класса разработана на основе федерального компонента государственного образовательного стандарта общего образования второго поколения. Стандарт первого поколения, утверждённый в 2004 году, по существу был, прежде всего, стандартом содержания образования, поскольку включал перечень тем, которые должен был изучить ученик по каждому предмету. Принципиальное отличие новых стандартов от стандартов первого поколения в том, что целью его реализации является не предметный, а личностный результат. Важна, прежде всего, личность самого ребёнка и происходящие с ним в процессе обучения изменения, а не сумма знаний, накопленная за время обучения в школе. Главной целью школьного образования является развитие ребенка как компетентной личности путем включения его в различные виды ценностной человеческой деятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.

Это определяет цели обучения математике в 8 классе:

• Развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов.

• Усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач.

• Овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин и для продолжения образования.

• Формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе.

• Формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.

Задачи учебного предмета:

• Развитие алгоритмического мышления.

• Овладение навыками дедуктивных рассуждений.

• Получение конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

• Формирование функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах.

• Понимание роли статистики как источника социально значимой информации.

• Приобретение конкретных знаний о пространстве и практически значимых умений.

• Формирование языка описания объектов окружающего мира.

• Развитие пространственного воображения и интуиции, математической культуры.

• Эстетическое воспитание учащихся.

• Развитие логического мышления.

• Формирование понятия доказательства.

Настоящая программа включает материал, создающий основу математической грамотности. Программа ориентирована на фундаментальный характер образования, динамична за счет вариативной составляющей, в нее включена характеристика учебной деятельности учащихся в процессе освоения содержания курса. В данной программе предусмотрено значительное увеличение активных форм работы, направленных на вовлечение учащихся в самостоятельную математическую деятельность, на обеспечение понимания ими математического материала и развития интеллекта, приобретение практических навыков, умений проводить рассуждения, доказательства. Наряду с этим в ней уделяется достаточное внимание использованию информационно-компьютерных технологий для усиления визуальной и экспериментальной составляющей обучения математике. Внедрение компьютерных технологий в учебный процесс преподавания математики в 8 классе позволит индивидуализировать процесс обучения за счет наличия разноуровневых заданий, за счет погружения и усвоения учебного материала в индивидуальном темпе, самостоятельно, используя удобные способы восприятия информации, что вызывает у учащихся положительные эмоции и формирует положительные учебные мотивы.

Рабочая программа по алгебре разработана для обучающихся8 класса. Учащиеся умеют воспринимать и анализировать информацию, представленную в различных формах. Владеют навыками проектной исследовательской деятельности, групповой работы, работы в парах, навыками работы в сети Интернет, на интерактивной доске.

Новизна данной программы определяется тем, что она предназначена для учащихся с разноуровневой подготовкой (обеспечивает уровневую дифференциацию обучения за счёт широкого диапазона заданий), перераспределены часы на изучение отдельных тем, пересмотрен подход к повторению учебного материала в конце года. Причиной перераспределения часов по некоторым темам явилась потребность в сохранении преемственности образования и актуализации знаний, что в первую очередь пригодится в практической жизни.

Формы организации учебного процесса:

индивидуальные, групповые, индивидуально-групповые, фронтальные.

Внеурочные формы: ВЗМШ, участие в работе школьного научного общества, участие в конференциях, конкурсах, олимпиадах и т.п.

Общая характеристика учебного предмета.

Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тен­денции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационноемком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Алгебра нацелена на формирование математического аппарата для решения задач математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира.

Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математическоймодели для описания и исследования разнообразных процессов (равномерных, равноускоренных и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.

Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.

Таким образом, в ходе освоения содержания курса учащиеся получают возможность:

развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;

овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;

изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;

получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;

развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;

сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.

Место учебного предмета «Алгебра-8» в учебном плане.

Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 ч из расчета 5 ч в неделю с V по IX класс.

Для обеспечения учебного процесса взята авторская программа общеобразовательных учреждений составитель Т.А. Бурмистрова .

В 7 классе выбран учебник «Алгебра, 7 класс» под редакцией Г.В. Дорофеева, Москва, «Просвещение»,2012г. По базисному учебному плану на курс «Алгебра, 7 класс» отведено 3 часа в неделю, всего 102 часа.

В 8 классе выбран учебник «Алгебра, 8 класс» под редакцией Г.В. Дорофеева, Москва, «Просвещение»,2014г. По базисному учебному плану на курс «Алгебра, 8 класс» отведено 3 часа в неделю, всего 102 часа.

В 9 классе выбран учебник «Алгебра, 9 класс» под редакцией Г.В. Дорофеева, Москва, «Просвещение»,2014г. Годовой объем учебного времени составляет 102 часа, недельная нагрузка 3 часа.

УМК Дорофеев В.Г.

Учебники соответствуют федеральным компонентам Государственного стандарта общего образования по математике. В курсе продолжается развитие вычислительной культуры школьников в ее современном понимании, активно формируется алгебраический аппарат, причем учащиеся овладевают более широким и практически значимым кругом умений, чем при изучении традиционного курса. При введении буквенного исчисления пересмотрено соотношение алгебраического и функционального подходов в пользу первого, что существенно упрощает трудный для учащихся материал и ускоряет овладение техникой преобразований. Функциональную линию отличает ярко выраженная прикладная направленность, а также постоянная взаимосвязь аналитического и графического аспектов; графические представления по мере их развития естественным образом встраиваются в другие разделы курса. Последовательно проводится содержательно-методическая линия, включающая комбинаторику, элементы теории вероятностей и статистику, которая органично сочетается с традиционными вопросами курса и существенно усиливает его практическое и прикладное значение. Особенностью курса является возможность осуществления в ходе преподавания уровневой дифференциации. Это достигается за счет широкого диапазона уровня сложности заданий, распределенных в группы А и Б. Через все книги проходит сквозная рубрика «Для тех, кому интересно», углубляющая и расширяющая учебный материал. Каждую главу завершают «Задания для самопроверки», отражающие уровень обязательной подготовки по данной теме и тест. Принятые при построении курса методические подходы направлены на обеспечение осознанности при изучении материала, формирование системных знаний, овладение набором разнообразных стратегий решения задач. В соответствии с требованиями личностно ориентированного обучения в учебниках принят живой стиль изложения, приводятся образцы рассуждений, указания и советы, развернутые алгоритмы действий. В результате ученик может самостоятельно получать из них нужную информацию, приобретать навыки работы с книгой.

Результаты освоения учебного предмета и система оценивания.

Изучение алгебры в основной школе даст возможность обучающимся достичь следующих результатов развития:

в личностном направлении:

1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;

2) критичность мышления, умение отличать гипотезу от факта;

3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;

4) креативность мышления, инициатива, находчивость, активность при решении задач;

5) умение контролировать процесс и результат учебной деятельности;

6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

в метапредметном направлении:

1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;

2) умение видеть математическую задачу в других дисциплинах, в окружающей жизни;

3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме;

4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;

6) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;

7) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;

8) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;

в предметном направлении:

1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;

2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;

3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками  устных, письменных, инструментальных вычислений;

4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;

5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;

6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;

7) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.

В результате изучения курса ученик научится:

— выполнять устно арифметические действия: сложение и вы­читание двузначных чисел и десятичных дробей с двумя зна­ками, умножение однозначных чисел, арифметические опера­ции с обыкновенными дробями с однозначным знаменателем и числителем;

— переходить от одной формы записи чисел к другой, представ­лять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты в ви­де дроби и дробь в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;

— выполнять арифметические действия с рациональными числа­ми, сравнивать рациональные и действительные числа; нахо­дить в несложных случаях значения степеней с целыми показа­телями и корней; находить значения числовых выражений;

— округлять целые числа и десятичные дроби, находить при­ближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;

— пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные едини­цы через более мелкие и наоборот;

— решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и про­центами;

— составлять буквенные выражения и формулы по условиям за­дач; осуществлять в выражениях и формулах числовые под­становки и выполнять соответствующие вычисления, осуще­ствлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

— выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; квадратными уравнениями, выполнять разложение многочленов на множители; квадратного трехчлена на множители, выполнять тождественные преобразования рациональных выражений;

— применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

— решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;

— решать линейные и квадратные неравенства с одной переменной и их системы;

— решать текстовые задачи алгебраическим методом, интерпре­тировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

— изображать числа точками на координатной плоскости;

— определять координаты точки плоскости, строить точки с за­данными координатами; изображать множество решений ли­нейного неравенства;

— распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и сум­мы нескольких первых членов;

— находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

— описывать свойства изученных функций, строить их графики;

— проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использо­вать примеры для иллюстрации и контрпримеры для опровер­жения утверждений;

— извлекать информацию, представленную в таблицах, на диа­граммах, графиках; составлять таблицы, строить диаграммы и графики;

— решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;

— вычислять средние значения результатов измерений;

— находить частоту события, используя собственные наблюде­ния и готовые статистические данные;

— находить вероятности случайных событий в простейших слу­чаях;

—использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: 

• решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных мате­риалов, калькулятора, компьютера; устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;

• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследования по­строенных моделей с использованием аппарата алгебры;

• описания зависимостей между физическими величинами при исследовании несложных практических ситуаций;

• интерпретации графиков реальных зависимостей между вели­чинами;

• выстраивания аргументации при доказательстве и в диалоге;

• распознавания логически некорректных рассуждений;

• записи математических утверждений, доказательств;

• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;

• решения практических задач в повседневной и профессио­нальной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;

• решения учебных и практических задач, требующих система­тического перебора вариантов;

• сравнения   шансов   наступления   случайных   событий,   для оценки вероятности случайного события в практических си­туациях, сопоставления модели с реальной ситуацией; понимания статистических утверждений.

Планируемые результаты учебного предмета.

В результате изучения алгебры ученик должен:

• выполнять действия с алгебраическими дробями, действия со степенями с целым показателем; развить навыки решения текстовых задач алгебраическим методом;

• преобразовывать выражения, со­держащие квадратные корни; на примере квадратного и кубиче­ского корней иметь представление о корне п-й степени;

• решать квадратные уравнения и использовать их при решении текстовых задач;

• иметь понятия уравнения с двумя пе­ременными, графика уравнения, системы уравнений;

• уметь ре­шать системы линейных уравнений с двумя переменными, а так­же использовать приемы составления систем уравнений при решении текстовых задач;

• иметь понятие о функции, пользоваться математическим языком, функциональной терминологией и символикой; знать свойства и гра­фики конкретных числовых функций: линейной функции и функции у = k\x; знать значимость функционального аппарата для моделирования реальных ситуаций, в несложных случаях применять полученные знания для решения прикладных и практических задач;

• иметь представление о возмож­ностях описания и обработки данных с помощью различных средних; вычислять вероятности случайного события с помощью классической формулы и из гео­метрических соображений

• существо понятия математического доказательства; примеры доказательств.

• существо понятия алгоритма; примеры алгоритмов.

• как используются математические формулы для решения математических и практических задач;

• как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

• как потребности практики привели математическую науку к необходимости расширения понятия числа;

• вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

• выполнять тождественные преобразования рациональных выражений;

• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

• решать линейные и рациональные уравнения, сводящиеся к ним.

• решать системы линейных уравнений с двумя переменными;

• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу.

• находить значение аргумента по значению функции, заданной графиком или таблицей;

• определять свойства функции по ее графику; применять графические представления при

• описывать свойства изученных функций, строить их графики; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами;

• нахождения нужной формулы в справочных материалах;

• моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.

Курс характеризуется рациональным сочетанием логической строгости и математической наглядности. Увеличивается теоретическая значимость изучаемого материала. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Систематическое изложение курса позволяет начать работу по формированию представлений учащихся о строении математической теории, обеспечивает развитие логического мышления.

Изложение материала характеризуется постоянным обращением к наглядности. Использованием рисунков и чертежей на всех этапах обучения и развитием математической интуиции на этой основе. Целенаправленное обращение к приемам из практики развивает умение учащихся выделять математические факты, формы и отношения в предметах и явлениях действительности, использовать язык математики для их описания.

Оценка письменных контрольных работ.

Ответ оценивается отметкой «5», если:

работа выполнена полностью;

в логических рассуждениях и обосновании решения нет пробелов и ошибок;

в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Оценка устных ответов.

Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

отвечал самостоятельно, без наводящих вопросов учителя;

возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;

имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;

обнаружено незнание учеником большей или наиболее важной части учебного материала;

допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

3. Общая классификация ошибок

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

незнание наименований единиц измерения;

неумение выделить в ответе главное;

неумение применять знания, алгоритмы для решения задач;

неумение делать выводы и обобщения;

неумение читать и строить графики;

неумение пользоваться первоисточниками, учебником и справочниками;

потеря корня или сохранение постороннего корня;

отбрасывание без объяснений одного из них;

равнозначные им ошибки;

вычислительные ошибки, если они не являются опиской;

логические ошибки.

3.2. К негрубым ошибкам следует отнести:

неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

неточность графика;

нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

нерациональные методы работы со справочной и другой литературой;

неумение решать задачи, выполнять задания в общем виде.

3.3. Недочетами являются:

нерациональные приемы вычислений и преобразований; небрежное выполнение записей, чертежей, схем, графиков.

Основное содержание учебного предмета. Алгебра – 7.

1. Алгебраические дроби - 23 часа.

Конструировать алгебраические выражения. Находить область определения алгебраической дроби; выполнять числовые подстановки и вычислять значение дроби, в том числе с помощью калькулятора. Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей. Выполнять действия с алгебраическими дробями. Применять преобразования выражений для решения задач Выражать переменные из формул {физических, геометрических, описывающих бытовые ситуации). Проводить исследования, выявлять закономерности. Формулировать определение степени с целым показателем. Формулировать, записывать в символический формeи иллюстрировать примерами свойства степени с целым показателем применять свойства степени для преобразования выражений и вычислений. Использовать запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивать числа и величины, записанные с использованием степе­ни 10. Выполнять вычисления с реальными данными. Выполнять прикидку и оценку результатов вычислений. Решать уравнения с дробными коэффициентами, решать текстовые задачи алгебраическим методом.

2. Квадратные корни - 21 час.

Формулировать определения квадратного корня из числа. Применять график функции у= х² для нахождёния корней квадратных уравнений, используя при необходимости калькулятор; проводить оценку квадратных корней. Строить график функции у=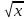,исследовать по графику её свойства. Доказывать свойства арифметических квадратных корней; применять их к преобразованию выражений. Вычислять значения выражений, содержащих квадратные корни; выполнять знаково-символические действия с использованием обозначений квадрат­ного и кубического корня: 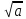, 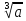.Исследовать уравнение вида х²=а. Находить точные и приближённые значения квадратных и кубических корней при а 0.

Формулировать определение корня третьей степени; находить; значения кубических корней, при необходимости используя калькулятор.

3.Квадратные уравнения - 18 часов.

Распознавать квадратные уравнения, классифицировать их. Выводить формулу корней квадратного уравнения. Решать квадратные уравнения — полные и неполные. Проводить простейшие исследования квадратных уравнений. Решать уравнения, сводящиеся квадратным, путём преобразований, а также с помощью замены переменной. Наблюдать и анализировать связь между корнямии коэффициентами квадратного уравнения. Формулировать и доказывать теорему Виета, а также обратная теорема, применять эти теоремы для решения разнообразных задач. Решать текстовые задачи алгебраическим способом; переходит от словесной формулировки усло­вия задачи к алгебраической мод ели путём состав­ления уравнения; решать составленное уравнение; интерпретировать результат. Распознавать квадратный трёхчлен, выяснять воз­можность разложения на множители, представлять квадратный трёхчлен в виде произведения линейных множителей. Применять различные приёмы самоконтроля при выполнении преобразований. Проводить исследования квадратных уравнений с буквенными коэффициентами, выявлять законо­мерности

4. Системы уравнений - 18 часов.

Определять, является ли пара чисел решением уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными. Решать задачи, алгебраической моделью которых является уравнение с двумя переменными; нахо­дить целые радения путём перебора.

Распознавать линейные уравнения с двумя пере­менными; строить прямые — графики линейных уравнений; извлекать из уравнения вида у=кх+1 информацию о положении прямой в координатной плоскости. Распознавать параллельные и пересе­кающиеся прямые по их уравнениям; конструиро­вать уравнения прямых, параллельных данной пря­мой. Использовать приёмы самоконтроля при построении графиков линейных уравнений. Решать системы двух линейных уравнений с двумя переменными; использовать графические пред­ставления для исследования систем линейных уравнений; решать простейшие системы, в кото­рых одно из уравнений не является линейный. Применять алгебраический аппарат для решения задач на координатной плоскости, решать тексто­вые задачи алгебраическим способом; переходить от словесной формулировки условия задачи к ал­гебраической модели путём составления системы уравнений; решать составленную систему уравне­ний; интерпретировать результат.

5. Функции - 14 часов.

Вычислять значение функций, заданных формулами (при необходимости использовать калькулятор); составлять таблицы значений функции.

Строить по точкам графики функций. Описывать свойства функции на основе ее графического представления.

Моделировать реальные зависимости формулами и графиками. Читать графики реальных зависимо­стей. Использовать функциональную символику для запи­си разнообразных фактов, связанных с рассматри­ваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Использовать компьютерные программы для по- строения графиков функций, для исследования положений на координатной плоскости графиков функций в зависимости от значений коэффициен­тов, входящих в формулу. Распознавать виды изучаемых функций. Показывать схематически расположение на координатной плоскости графиков функций вида у=кх, у=кх + Ь,у =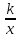, в зависимости от значений коэффициентов, входящих в формулы. Строить графики изучаемых функций; описывать их свойства.

6. Вероятность и статистика - 4 часов.

Характеризовать числовые ряды с помощью раз­личных средних. Находить вероятности событий при равновозможных исходах; решать задачи на вычисление вероятностей с применением комби­наторики. Находить геометрические вероятности.

5. Повторение – 4 часов.

Ключевые темы курса «Алгебра» - 8 класс. Алгебраические дроби, квадратные уравнения, системы уравнений, функции.

Тематическое планирование с определением основных видов учебной деятельности.

Алгебра -8.

№ урока	Дата	Домашнее задание	Тема	Содержание	Деятельность обучающихся на уроке. (Виды, формы, способы деятельности).	Планируемый результат
Алгебраические дроби (23 часа)
1. 2.			Алгебраическая дробь.	Алгебраическая дробь. Множество допустимых значений.	Составление опорного конспекта индивидуально,  коллективная работа с текстом учебника. Формирование у обучающихся умений построения и реализации новых знаний. Проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать алгоритм дейст­вий с алгебраическими дробями. Уметь распознавать алгебра­ическую дробь среди других буквенных выра­жений; приводить примеры алгебраических дробей, в несложных случаях. Вычислять значение алгебраической дроби при указанных значениях переменных; находить множество допустимых значений переменных, входящих в данную дробь.
3. 4. 5.			Основное свойство дроби.	Основное свойство алгебраической дро­би. Сокращение дробей. Приведение дробей к общему знаменателю.	Тест, набор карточек с алгоритмами решений упражнений. Формирование у учащихся способности к рефлекторной деятельности : ответы на вопросы по домашнему заданию (разбор нерешенных задач), контроль усвоения материала (письменный опрос), построение алгоритма действий, выполнение практических заданий из УМК	Знать можно ли обыкновенную дробь представить в виде десятичной. Знать приёмы выполнения действий с числами. Уметь свободно переходить от десятичных дробей к обыкновенным; находить десятичные эквиваленты, десятичные приближения обыкновенных дробей; применять калькулятор.
6. 7. 8. 9. 10.			Сложение и вычитание алгебраических дробей.	Правила сложения и вычитания алгебраических дробей.	Работа с текстом учебника. Интеллект-карта по теме. Формирование у учащихся деятельностных способностей и способностей к структурированию и систематизации изучаемого предметного содержания; индивидуальная работа - составление опорного конспекта по теме урока, фронтальный опрос по готовому конспекту. Проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать правила сложения и вычитания алгебраических дробей и уметь ими пользоваться при выполнении упражнений.
11. 12. 13.			Умножение и деление алгебраических дробей.	Правила умножения и деления алгебраических дробей.	Чтение текста и воспроизведение ключевых моментов. Формирование у учащихся способностей к рефлексии коррекционно-контрольного типа и реализации коррекционной нормы: разбор нерешенных задач, работа по дифференцированным карточкам из УМК, проектирование выполнения домашнего задания, комментирование выставленных оценок. Фронтальная, индивидуальная работа.	Знать правила умножения и деления алгебраических дробей. Уметь применять правила при преобразовании выражений, содержащих алгебраические дроби.
14. 15.	.		Преобразование выражений, содержащих алгебраические дроби.	Сокращение дробей. Сложение, вычитание, умножение и деление алгебраических дробей.	Опросники самодиагностики усвоения материала по теме. Таблица алгоритмов решения разных типов задач. Выполнение творческого задания, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать законы алгебры; какие выражения называются тождественно равными. Уметь выполнять замену одного буквенного выражения другим; упрощать выражения; составлять алгебраическую сумму, уметь определять множество допустимых значений переменных.
16. 17.			Степень с целым показателем.	Степень с целым показателем и ее свойства. Выделение множителя — степени десяти — в записи числа. Стандартный вид числа.	Работа с учебником, дополнительной литературой, демонстрационным материалом. Формирование у учащихся деятельностных способностей и способностей к структурированию и систематизации изучаемого предметного содержания; индивидуальная работа. Контроль и самоконтроль изученных понятий: заполнение вопросника по самодиагностики.	Знать определение степени с целым показателем; стандартный вид числа. Уметь вычислять значе­ния выражений, содер­жащих степени. Уметь пользоваться определением степени для записи выражений более компактно.
18. 19.			Свойства степени с целым показателем.	Свойства степени с целым показателем. Миллиардная часть метра – нанометр.	Работа с текстом учебника - коллективная. Просмотр презентаций (домашнее задание). Формирование у обучающихся умений построения и реализации новых знаний: устный опрос, выполнения практических заданий из УМК, проектирование выполнения домашнего задания, комментирование выставленных оценок. Составление опорного конспекта по теме урока.	Знать свойства степени, уметь записывать свойства с использованием принятых символических обозначений. Уметь использовать свойства при преобразовании комбинированных буквенных выражениях.
20. 21. 22.			Решение уравнений и задач.	Решение линейных уравнений, коэффициентами которых являются обыкновенные или десятичные дроби. Уравнения, составленные из алгебраических дробей. Решение задач с использованием линейных уравнений.	Работа по готовым таблицам. Выполнение нестандартных упражнений по группам. Формирование у учащихся навыков самодиагностирования и взаимоконтроля. Комментирование выставленных оценок. Фронтальная, индивидуальная работа при решении упражнений,  ответы на вопросы.	Уметь решать уравнения; применять алгебраиче­ский метод для решения текстовых задач.
23.			Контрольная работа №1 по теме: «Алгебраические дроби».	Сложение и вычитание, умножение и деление алгебраических дробей. Преобразование выражений, содержащих алгебраические дроби. Свойства степени с целым показателем.	Тест с теоретическими заданиями и практическими упражнениями с 4 ответами на выбор правильного.	Знать основные понятия темы, основное свойство дроби, правила действий с дробями. Уметь преобразовывать алгебраические дроби, находить множество допустимых значений переменной в алгебраической дроби.
Квадратные корни (21 час)
24. 25.			Задача о нахождении стороны квадрата.	Квадратный корень. Площадь квадрата. Символ √	Практическая работа в группах. Составление опорного конспекта,  работа с текстом и книгой. Выполнение творческого задания, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать/понимать как потребности прак­тики привели математи­ческую науку к необхо­димости расширения понятия числа; определение квадрат­ного корня; терминологию. Уметь извлекать квадратные корни; оценивать неизвлекающиеся корни; находить приближен­ные значения корней как с помощью калькуля­тора, так и с помощью оценки значений.
26. 27.			Иррациональные числа.	Иррациональные числа. Действитель­ные числа.	Работа с демонстрационным материалом. Формирование у учащихся умений построение и реализации новых знаний (понятий, способов действий и т.д.): фронтальная беседа с классом, работа у доски и в тетрадях, работа с УМК.	Знать и понимать какие числа иррациональные, какие рациональные, какой вид они имеют. Множество действительных корней. Уметь находить приближенные значения квадратных корней, округлять числа до соответствующего разряда.
28. 29. 30.			Теорема Пифагора.	Теорема Пифагора. Решение задач с применением теоремы Пифагора.	Индивидуальные карточки с дифференцированными заданиями. Формирование у учащихся способности к рефлекторной деятельности : разбор нерешенных задач, построение алгоритма действий, составление опорного конспекта по теме урока, работа с опорным конспектом, выполнение практических заданий в группах. Проектирование выполнения домашнего задания, комментирование выставленных оценок. Групповая, индивидуальная работа. Решение задач.	Знать как потребности прак­тики привели математи­ческую науку к необхо­димости расширения понятия числа; определения квадрат­ного корня. Знать терминологию. Уметь извлекать квадратные корни; оценивать значения корней из числа, результатом которого является иррациональное число. Находить приближен­ные значения корней.
31. 32. 33. 34.			Квадратный корень (алгебраический подход).	Опреде­ление квадратного корня. Арифметиче­ский квадратный ко­рень. Число решений уравнения х2= а.	Составление опорного конспекта,  работа с текстом и книгой. Оценочная шкала. Формирование у учащихся способности к рефлексивной деятельности : разбор нерешенных задач, фронтальный опрос, выполнение практических заданий из УМК, выполнение творческого задания, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать определение квадратного корня, арифметического квадратного корня. Уметь находить приближен­ные значения корней как с помощью калькуля­тора, так и с помощью оценки.
35. 36. 37.			График зависимости y=. Свойства квадратных корней.	Графики зависимостей y= , y = . Симметрия графиков. Свойства зависимостей. Теоремы о корне из произведения и частного.	Презентации, работа с демонстрационным материалом. Заполнение готовых таблиц по теме. Вопросник по темам ранее изученного материала (контроль ЗУН по ранее изученному материалу). Формирование у учащихся умений построения и реализации новых знаний. Групповая, индивидуальная работа. Решение упражнений из УМК.	Знать формулировки свойств. Уметь записывать свойства в символической форме; применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни.
38. 39. 40.			Преобразование выражений, содержащих квадратные корни.	Подобные радикалы. Равенство. Освобождение от иррациональности в знаменателе дроби.	Тесты, таблицы, опросники самодиагностики. Выполнение практических заданий по дифференцированным карточкам.	Знать формулировки свойств. Уметь записывать свойства в символической форме; применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни.
41. 42. 43.			Кубический корень.	Определение кубического корня. Зависимость y=. Кубическая парабола. – корень n-ой степени.	Работа с текстом учебника. Формирование у учащихся способности к рефлексивной деятельности : разбор нерешенных задач, фронтальный опрос, выполнение практических заданий из УМК, выполнение творческого задания, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать определение кубического корня, корня н-ой степени. Уметь находить кубический корень с использованием калькулятора.
44.			Контрольная работа №2 по теме: "Квадратные корни".	Квадратные корни, корни n-ой степени, графики зависимостей: y= , y= .Преобразования выражений, содержащих радикалы. Избавление от иррациональности в знаменателе.	Тест по 4 вариантам. Индивидуальная работа. Формирование у обучающих умений к осуществлению контрольной функции ; контроль и самоконтроль изученных понятий: написание контрольной работы.	Знать основные понятия темы: «Квадратные корни».
Квадратные уравнения (18 часов)
45. 46.			Какие уравнения называются квадратными.	Квадратное уравнение. Коэффициенты. Приведенное квадратное уравнение	Построение алгоритма действий, выполнение практических заданий. Индивидуальные проверочные карточки по пройдённой теме. Просмотр презентаций, подготовленных обучающимися (групповая творческая работа).	Знать определение квадратного уравнения; что первый коэффициент не может быть равен нулю. Уметь записать квадратное уравнение в общем виде; неприведенное квадратное уравнение преобразовывать в приведенное квадратное уравнение, свободно владеть терминологией.
47. 48. 49.			Формула корней квадратного уравнения.	Формула корней квадратного уравнения. Дискриминант. Знак дискриминанта и число корней.	Работа с текстом учебника. Групповая и индивидуальная работа. Решение алгоритмических задач. Решение индивидуальных дифференцированных заданий, с последующей проверкой по таблице ответов.	Распознавать квадратные уравнения, классифицировать их. Выводить формулу корней квадратного уравнения. Решать квадратные уравнения — полные и неполные. Проводить простейшие исследования квадратных уравнений. Решать уравнения, сводящиеся к квадратным, путём преобразований, а также с помощью замены переменной. Наблюдать и анализировать связь между корнями и коэффициентами квадратного уравнения.
50. 51. 52.			Вторая формула корней квадратного уравнения.	Квадратные уравне­ния с четным вто­рым коэффициен­том. Уравнения высших степеней.	Составление опорного конспекта,  работа с текстом учебника. Самостоятельное выполнение практической работы по выводу второй формулы корней квадратного уравнения. Формирование у учащихся навыков самодиагностирования и взаимоконтроля. Комментирование выставленных оценок.	Знать формулу корней квадратного уравнения с четным вторым коэффициентом. Уметь решать квадратные урав­нения по формуле I, II; решать уравнения выс­ших степеней заменой переменной.
53. 54. 55.			Решение задач.	Текстовые задачи с арифметическим, геометрическим, физическим содержа­нием, с экономиче­скими фабулами. Ма­тематическая модель. Применение при решении задач квадратных уравнений.	Тест к главе: « Уравнения». Фронтальная, индивидуальная работа. Решение упражнений,  ответы на вопросы. Формирование у учащихся способности к рефлексивной деятельности : разбор нерешенных задач, выполнение творческого задания, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Решать текстовые задачи алгебраическим способом; переходит от словесной формулировки усло­вия задачи к алгебраической модели путём состав­ления уравнения; решать составленное уравнение; интерпретировать результат.
56. 57.			Неполные квадратные уравнения.	Неполные квадрат­ные уравнения. Приемы решения уравнений.	Индивидуальная работа по готовым карточкам с дифференцированными заданиями. Выполнение проблемных и практических заданий в группах.	Знать термин «неполное квадратное уравнение»; приемы решения неполных квадратных уравнений. Уметь распознавать и решать неполные квад­ратные уравнения.
58. 59.			Теорема Виета.	Теорема Виета. Формулы Виета. Теорема, обратная теореме Виета.	Творческое задание для самостоятельного выведения формул (Теоремы Виета). Просмотр презентации: биография французского математика Франсуа Виета. (коллективная домашняя работа группы). Шкала «настроения». Фронтальная беседа с классом, работа у доски и в тетрадях, работа с УМК.	Формулировать и доказывать теорему Виета, а также обратную теорему, применять эти теоремы для решения разнообразных задач.
60. 61.			Разложение квадратного трёхчлена на множители.	Определение квадратного трехчлена. Дискриминант квадратного трехчлена. Корни квадратного трехчлена. Разложение квадратного трёхчлена на множители.	Дополнительный материал (подборка нестандартных задач). Решение практических и нестандартных заданий в группах, комментирование решения от группы у доски. Формирование у учащихся умений построение и реализации новых знаний (понятий, способов действий и т.д.): фронтальная беседа с классом, работа у доски и в тетрадях, работа с УМК.	Распознавать квадратный трёхчлен, выяснять воз­можность разложения на множители, представлять квадратный трёхчлен в виде произведения линейных множителей. Применять различные приёмы самоконтроля при выполнении преобразований. Проводить исследования квадратных уравнений с буквенными коэффициентами, выявлять законо­мерности.
62.			Контрольная работа №3 по теме: "Квадратные уравнения".	Квадратные уравнения. Теорема Виета. Задачи.	Решение контрольной работы в форме теста. Тесты с двумя частями: теоретическая часть с заданием ответить на 4 вопроса (ответ "да" или "нет") и практическая часть с выбором ответа из четырех предложенных.	Знать определение квадратного уравнения, дискриминанта. Формулы корней квадратного уравнения. Уметь находить корни, используя формулы, а также другие способы для отдельных видов квадратных уравнений. Уметь раскладывать квадратный трехчлен на множители. Уметь применять теорему Виета и теорему, обратную теореме Виета.
Системы уравнений (18 часов)
63. 64. 65.			Линейное уравнение с двумя переменными.	Определение линейного уравнения с двумя переменными. Решение уравнений с двумя переменными. Что называется решением уравнения с двумя переменными.	Формирование у обучающих умений к осуществлению контрольной функции ; контроль и самоконтроль изученных понятий: заполнений карты понятий по пройденной теме: "Квадратные уравнения", после анализа контрольной работы. Индивидуальная работа с текстом учебника, составление опорного конспекта.	Определять, является ли пара чисел решением уравнения с двумя переменными; приводить примеры решений уравнений с двумя переменными. Решать задачи, алгебраической моделью которых является уравнение с двумя переменными; нахо­дить целые радения путём перебора. Распознавать линейные уравнения с двумя пере­менными.
66. 67. 68.			График линейного уравнения с двумя переменными. Уравнения прямой вида: y=kx+l.	График уравнения вида: ax + by = c. Графики зависимостей: y=kx и y=kx+l. Взаимное расположение прямых линейного уравнения в зависимости от коэффициентов.	Модели координатной плоскости». Слайды «Графики». Составление опорного конспекта. Работа с демонстрационным материалом. Формирование у учащихся способностей к рефлексии коррекционно-контрольного типа и реализации коррекционной нормы: выполнение практических заданий из УМК, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать и понимать, что такое уравнение прямой, алгоритм построения прямой. Уметь строить прямые — графики линейных уравнений; извлекать из уравнения вида у=кх+1 информацию о положении прямой в координатной плоскости. Распознавать параллельные и пересе­кающиеся прямые по их уравнениям; конструиро­вать уравнения прямых, параллельных данной пря­мой. Использовать приёмы самоконтроля при построении графиков линейных уравнений.
69. 70. 71.			Системы уравнений. Решение систем способом сложения.	Условия параллельности прямых. Система уравнений. Решение систем уравнений с двумя переменными способом сложения. .	Индивидуальный опрос. Построение алгоритма действий, выполнение заданий. Решение упражнений с комментарием у доски - коллективная работа. Проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать определение системы двух линейных уравнений, что значит решить систему. Уметь решать системы двух линейных уравнений с двумя переменными; использовать графические пред­ставления для исследования систем линейных уравнений; решать простейшие системы, в кото­рых одно из уравнений не является линейный. Знать способ решения системы: способ сложения.
72. 73. 74.			Системы уравнений. Решение систем способом подстановки..	Способ записи сис­тем с помощью фи­гурной скобки. Ре­шение систем спосо­бом сложения и спо­собом подстановки.	Шаблоны решений систем уравнений разного типа. Подбор заданий для групп с разными учебными возможностями. Формирование у учащихся способностей к рефлексии коррекционно-контрольного типа УМК.	Знать и понимать, что если графики имеют общую точку, то система имеет решение, если не имеет, то система не имеет решение. Знать алгоритм решения систем уравнений. Уметь решать систему способом подстановки.
75. 76. 77.			Решение задач с помощью систем уравнений.	Математическая мо­дель задачи. Система уравнений. Решение уравнения или сис­темы уравнения. Соответствие полу­ченного результата условию задачи	Работа с текстом учебника. Презентации : "Решение систем разными способами", работа с демонстрационным материалом, выполнение практических заданий из УМК. Фронтальная, индивидуальная работа. Решение упражнений,  ответы на вопросы.	Уметь применять алгебраический аппарат для решения задач на координатной плоскости, решать тексто­вые задачи алгебраическим способом; переходить от словесной формулировки условия задачи к ал­гебраической модели путём составления системы уравнений; решать составленную систему уравне­ний; интерпретировать результат.
78. 79.			Задачи на координатной плоскости.	Применение алгеб­раического аппарата к решению задач с геометрической тематикой. Коорди­наты точки пересе­чения прямых.	Математический диктант, с последующей проверкой с помощью интерактивной доски. Формирование у обучающих умений к осуществлению контрольной функции ; контроль и самоконтроль изученных понятий.	Знать геометрический смысл коэффициентов; условие параллельно­сти прямых. Уметь свободно решать системы линейных
80.			Контрольная работа №4 по теме: "Системы уравнений".	Линейное уравнение с двумя переменными. Графики уравнений вида: ax+by=c иax=by. Системы уравнений с двумя переменными. Задачи.	Решение контрольной работы по вариантам. Проектирование выполнения домашнего задания, комментирование выставленных оценок	Уметь использовать полученные знания по теме при решении типовых и нестандартных заданий.
Функции (14 часов)
81. 82.			Чтение графиков.	Графики функции. Графические харак­теристики - сравне­ние скоростей, вы­числение скоростей, определение макси­мальных и мини­мальных значений.	Презентация «Графики вокруг нас». Формирование у учащихся деятельностных способностей и способностей к структурированию и систематизации изучаемого предметного содержания; индивидуальная работа; составление опорного конспекта по теме урока.	Уметь находить с помощью графика значение одной из рассматриваемых вели­ чин по значению другой; описывать характер изменения одной вели­чины в зависимости от другой; строить график зависимости, если одна задана таблицей. Строить по точкам графики функций. Описывать свойства функции на основе ее графического представления. Моделировать реальные зависимости формулами и графиками. Читать графики реальных зависимо­стей.
83. 84.			Что такое функция. График функции.	Что такое функция. Зависимые, независимые переменны. Координаты. Абсцисса и ордината. Область определения функции. График функции.	Таблицы с теоретическими вопросами по заполнению пропущенных ячеек. Формирование у учащихся способности к рефлексивной деятельности : разбор нерешенных задач, устный опрос, выполнение практических заданий из УМК. Индивидуальна работа, работа в парах (по заполнению таблиц).
85. 86. 87.			Свойства функции.	Свойства функции. Наибольшее и наименьшее значения функции. Положительные и отрицательные значения функции. Функция возрастает, убывает.	Работа с учебником и дополнительной математической литературой, выполнение заданий на закрепление теоретического материала. Опрос по теоретическому материалу, работа с демонстрационным материалом.	Знать/понимать терми­ны «функция», «аргу­мент», «область опреде­ления функции». Уметь записывать функцио­нальные соотношения с использованием симво­лического языка: у =f(х), f(З),f(х) = х2-2; находить по формуле значение функции, соот­ветствующее данному аргументу.
88. 89. 90.			Линейная функция.	Определение линейной функции. График линейной функции. Свойства линейной функции. График постоянной функции.	Составление опорного конспекта,  работа с текстом и книгой. Формирование у обучающихся умений построения и реализации новых знаний: устный опрос, выполнения практических заданий из УМК, коллективная исследовательская работа, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Уметь строить график линей­ ной функции; определять, возраста­ющей или убывающей является линейная функция; находить с помощью графика промежутки знакопостоянства. Распознавать виды изучаемых функций. Показывать схематически расположение на координатной плоскости графиков функций вида у=кх, у=кх + Ь,у =к\х, в зависимости от значений коэффициентов, входящих в формулы. Строить графики изучаемых функций; описывать их свойства
91. 92. 93.			Функция y=и ее график.	Функция обратной пропорциональности. График функции. Свойства функции.	Презентации (групповая домашняя работа) графики обратной пропорциональности. Формирование у учащихся деятельностных способностей и способностей к структурированию и систематизации изучаемого предметного содержания. Индивидуальная работа по составлению опорного конспекта по теме урока, фронтальный опрос, выполнение практических заданий из УМК, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Знать свойства функции обратной пропорциональности, функциональную сим­волику. Уметь строить график функции обратной пропорциональной зависимости; моделировать ситуацию.
94.			Контрольная работа №5 по теме: "Функция".	Функции. Построение графика функций. Формулировка свойств функций. Чтение графиков.	Решение контрольной работы по вариантам.	Знать основные функции и уметь строить их графики, описывать свойства и применять в практической ситуации.
Вероятность и статистика (4 часа)
95. 96.			Статистические характеристики.	Размах. Среднее арифметическое. Таблица частот. Мода. Медиана ряда.	Карточки с устными заданиями. Работа в парах. Формирование у учащихся способностей к рефлексии коррекционно-контрольного типа. Работа по дифференцированным карточкам из УМК, проектирование выполнения домашнего задания, комментирование выставленных оценок.	Понимать, как с помо­щью различных средних проводятся описание и обработка данных. Знать определение веро­ятности. Уметь составлять и анализи­ровать таблицу частот; находить медиану; распознавать равнове­роятные события; решать задачи на пря­ мое применение опреде­ления статистических характеристик.
97. 98.			Вероятность равновозможных событий.	Классическое опре­деление вероятно­сти. Способ вычис­ления вероятности события.	Фронтальный опрос, выполнение дифференцированных тестов. Индивидуальные тесты. Формирование у обучающих умений к осуществлению контрольной функции ; контроль и самоконтроль изученных понятий, заполнение тестов.	Характеризовать числовые ряды с помощью раз­личных средних. Находить вероятности событий при равновозможных исходах; решать задачи на вычисление вероятностей с применением комби­наторики. Находить геометрические вероятности.
Повторение (4 часа)
99.			Повторение. Алгебраические дроби. Квадратные уравнения.	Основное свойство дроби. Преобразование выражений, содержащих алгебраические дроби. Степень с целым показателем. Формула дискриминанта квадратного уравнения, формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена.	Составление карточек с правилами действий с алгебраическими дробями для их лучшего запоминания. Таблицы с пропущенными ячейками. Формирование у обучающихся умений систематизации ранее изученных знаний: составление опорных конспектов, фронтальный опрос, выполнение практических заданий из УМК, проектирование выполнения домашнего задания, комментирование выставленных оценок. Составление опорных карточек с алгоритмом решения задач с помощью уравнений.	Систематизировать полученные знания , знать и уметь составлять карты понятий по ключевым темам. Уметь применять знания при решении типовых и нестандартных заданий.
100.			Повторение. Системы уравнений. Функции.	Решение систем линейных уравнений с двумя переменными. График линейной функции.	Опорные карточки: применение способа сложения и способа подстановки для решения систем уравнений. Формирование у учащихся способностей к рефлексии коррекционно-контрольного типа Комментирование выставленных оценок.	Систематизировать полученные знания , знать и уметь составлять карты понятий по ключевым темам. Уметь применять знания при решении типовых и нестандартных заданий.
101.			Итоговая контрольная работа.	Основной теоретический материал за курс 8 класса.	Итоговый тест по ключевым темам курса алгебры 8 класса. Формирование у обучающих умений к осуществлению контрольной функции ; контроль и самоконтроль изученных понятий: написание контрольной работы
102.			Анализ контрольной работы Подведение итогов за год

Учебно – методическое и материально – техническое обеспечение образовательного процесса.

1.Основной список для учителя:

• Дорофеев Г.В. Алгебра, 8 кл., учебник для общеобразовательных учреждений/ Г.В. Дорофеев, С.Б. Суворова и др. – М.: Просвещение, 2014. Рекомендовано Министерством образования и науки Российской Федерации, соответствует обязательному минимуму содержания основного общего образования по математике.

• Минаева С. С. Алгебра, 8 кл.: рабочая тетрадь / С. С. Минаева, Л. О. Рослова.- М.: Просвещение, 2014.

• Евстафьева Л.П. Алгебра, 8 кл.: дидактические материалы / Л.П. Евстафьева, А. П. Карп .- М.: Просвещение, 2014.

• Кузнецова Л.В. Алгебра, 7-9 кл.: контрольные работы/ Л. В. Кузнецова, С. С. Минаева, Л.О. Рослова. - М.: Просвещение, 2011.

• Кузнецова Л. В. Алгебра, 8 кл.: тематические тесты. / Л. В. Кузнецова, С. С. Минаева, Л.О. Рослова. - М.: Просвещение, 2011.

• Дорофеев Г.В. Алгебра, 8 кл., книга для учителя / Г.В. Дорофеев, С. С. Минаева, С.Б. Суворова.- М.: Просвещение, 2011.

Дополнительный список для учителя:

• Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре для 8 класса. 6-е изд., стер. - СПб.: 2011.

• Федеральный центр информационно – образовательных ресурсов (ФЦИОР) http://fcior.edu.ru

• Единая коллекция цифровых образовательных ресурсов (ЕК) http://school-collection.edu.ru

• Федеральный портал «Российское образование» http://www.edu.ru

• Российский общеобразовательный портал http://www.school.edu.ru

• Федеральный портал «Информационно - коммуникационные технологии в образовании» http://www.ict.edu.ru

• Российский портал открытого образования http://www.openet.edu.ru

• Алгебра 8 под ред. Дорофеева Г.В. http://www.mathsolution.ru/books/99

• Математические этюды www.etudes.ru

• База данных задач по всем темам школьной математики www.problems.ru

• Фестиваль ученических работ «Портфолио» («Первое сентября») https://portfolio.1september.ru

• Интернет-журнал «Эйдос». Основные рубрики журнала: «Научные исследования», «Дистанционное образование», «Эвристическое обучение». www.eidos.ru/journal/content.htm

• Математика на портале «Открытый колледж» www.college.ru/mathematics

• Головоломки для умных людей. На сайте можно найти много задач (логических, на взвешивание и др.), вариации на тему кубика Рубика, электронные версии книг Р. Смаллиана, М. Гарднера, л. Кэрролла. www.golovolomka.hobby.ru

• Большая библиотека, содержащая как книги, так и серии брошюр, сборников по математике www.math.ru/lib

• Электронная версия журнала «Квант» www.kvant.mccme.ru

• Математические олимпиады и олимпиадные задачи для школьников. www.zaba.ru

• Сайт поддержки Международной математической игры «Кенгуру» www.kenguru.sp.ru

• Московский центр непрерывного математического образования www.mccme.ru

Список основной литературы для обучающихся:

• Дорофеев Г.В. Алгебра, 8 кл., учебник для общеобразовательных учреждений/ Г.В. Дорофеев, С.Б. Суворова и др. – М.: Просвещение, 2014. Рекомендовано Министерством образования и науки Российской Федерации, соответствует обязательному минимуму содержания основного общего образования по математике.

• Минаева С. С. Алгебра, 8 кл.: рабочая тетрадь / С. С. Минаева, Л. О. Рослова.- М.: Просвещение, 2014.

• Евстафьева Л.П. Алгебра, 8 кл.: дидактические материалы / Л.П. Евстафьева, А. П. Карп .- М.: Просвещение, 2011.

• Кузнецова Л. В. Алгебра, 8 кл.: тематические тесты. / Л. В. Кузнецова, С. С. Минаева, Л.О. Рослова. - М.: Просвещение, 2013.

Список дополнительной литературы для обучающихся:

• Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре для 8 класса. 6-е изд., стер. - СПб.: 2011.

• Алгебра 8 под ред. Дорофеева Г.В. http://www.mathsolution.ru/books/99

• Математические этюды www.etudes.ru

• База данных задач по всем темам школьной математики www.problems.ru

• Фестиваль ученических работ «Портфолио» («Первое сентября») https://portfolio.1september.ru

• Интернет-журнал «Эйдос». Основные рубрики журнала: «Научные исследования», «Дистанционное образование», «Эвристическое обучение». www.eidos.ru/journal/content.htm

• Головоломки для умных людей. На сайте можно найти много задач (логических, на взвешивание и др.), вариации на тему кубика Рубика, электронные версии книг Р. Смаллиана, М. Гарднера, л. Кэрролла. www.golovolomka.hobby.ru

• Электронная версия журнала «Квант» www.kvant.mccme.ru

• Математические олимпиады и олимпиадные задачи для школьников. www.zaba.ru

• Сайт поддержки Международной математической игры «Кенгуру» www.kenguru.sp.ru

2. Печатные пособия

1. Таблицы по математике

3. Учебно-практическое и учебно-лабораторное оборудование:

1. Доска с координатной сеткой.

2. Комплект чертежных инструментов (классных и раздаточных): линейка, транспортир, угольник (30°, 60°, 90°), угольник (45°, 90°), циркуль.

3. Шаблоны графиков различных зависимостей.