Методическая разработка для подготовки к сдаче ОГЭ
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
Неравенства и их системы
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Неравенства и их системы»
Введение
Основные типы преобразований неравенств...................................................4
Содержание и организация обучения решению неравенств и систем...........12
Методические особенности изучения основных классов неравенств и их систем.....................................................................................................................18
ГЛАВА 2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ФОРМИРОВАНИЮ УЧЕБНЫХ НАВЫКОВ ПРИ РЕШЕНИИ НЕРАВЕНСТВ И ИХ СИСТЕМ В ОСНОВНОЙ ШКОЛЕ...........................................................................................18
Пояснительная записка к элективному курсу «Неравенства и их системы в основной школе» 19
Особенности обучения решению неравенств и систем неравенств в рамках элективного курса 31
ЗАКЛЮЧЕНИЕ 40
БИБЛИОГРАФИЧЕСКИЙ СПИСОК..................................................................41
Учебное пособие для элективного курса «Неравенства и их системы в основной школе» 46
| | |
|
|
|
| | |
Значительную часть школьного курса математики составляет материал, который связан с неравенствами . Неравенства используются при решении важных прикладных задач, с их помощью математическим языком записываются различные задачи, связанные с реальной действительностью, используют при решении текстовы х задач ,при изучении свойств функций.
Цель: разработать методические рекомендации при подготовке к ОГЭ в рамках темы неравенств и их систем.
Задачи :
Определить основные типы преобразований неравенств и их систем.
Описать методические особенности изучения основных классов неравенств .
3.Разработать методику подготовки и программу по изучению данной темы в рамках подготовки к ОГЭ.
Большое значение имеет выяснение вопросов при выполнении преобразований: являются ли они равносильными или логическим следованием, требуется ли рассмотрение нескольких случаев, нужна ли проверка?
В основе решения неравенств с одной переменной лежит понятие равносильности.
Определение. Два неравенства называются равносильными, если их множества решений равны.Например, неравенства 2x + 7 10 и 2x 3 равносильны, так как их
множества решений равны и представляют собой промежуток (2 ; +∞).
3
Теоремы о равносильности неравенств и следствия из них аналогичны соответствующим теоремам о равносильности уравнений. При их доказательстве используются свойства истинных числовых неравенств [34].
Теорема 3. Пусть неравенство f(х) g(х) задано на множестве X и h(x)
выражение, определенное на том же множестве.
Тогда неравенства f(х) g(х) и f(х) + h(x) g(х) + h(x) равносильны на множестве X.
Из этой теоремы вытекают следствия, которые часто используются при решении неравенств:
Если к обеим частям неравенства f(х) g(х) прибавить одно и то же число d, то получим неравенство f(х) + d g(х) + d, равносильное исходному.
Если какое-либо слагаемое (числовое выражение или выражение с переменной) перенести из одной части неравенства в другую, поменяв знак слагаемого на противоположный, то получим неравенство, равносильное данному.
Теорема 4. Пусть неравенство f(х) g(х) задано на множестве X и h(х) - выражение, определенное на том же множестве, и для всех х из множества X выражение h(х) принимает положительные значения. Тогда неравенства f(х) g(х) и f(х)∙h(x) g(х)∙h(x) равносильны на множестве X.
Из этой теоремы вытекает следствие: если обе части неравенства
f(х) g(х) умножить на одно и то же положительное число d, то получим неравенство f(х)∙d g(х)∙d, равносильное данному [14].
Теорема 5. Пусть неравенство f(х) g(х) задано на множестве X и h(х) - выражение, определенное на том же множестве, и для всех х их множества X выражение h(х) принимает отрицательные значения. Тогда неравенства f(х) g(х) и f(х)∙h(x) g(х)∙h(x) равносильны на множестве X.
Из этой теоремы вытекает следствие: если обе части неравенства
f(х) g(х) умножить на одно и то же отрицательное число d и знак неравенства поменять на противоположный, то получим неравенство f(х)∙d g(х)∙d, равносильное данному [14].
Рассмотрим решение неравенств с одной переменной.
Решим неравенство 5х – 5 2х – 16, и обоснуем все преобразования, которые мы будем выполнять в процессе решения (табл.1).
Таблица 1
Преобразование неравенства 5х – 5 2х – 16
| Преобразования | Обоснование преобразования |
| 1. Перенесем выражение 2x в левую часть, а число –5 в правую, поменяв их знаки на противоположные: 5x – 2x | Воспользовались следствием 2 из теоремы 3, получили неравенство, равносильное данному. |
| 2. Приведем подобные члены в левой и правой частях неравенства: 3х | Выполнили тождественные преобразования выражений в левой и правой частях неравенства - они не нарушили равносильности неравенств: данного и исходного. |
| 3. Разделим обе части неравенства на 3: x | Воспользовались следствием из теоремы 4, получили неравенство, равносильное исходному. |
Решением неравенства х х – 5 х + 16 является промежуток (– ∞, 7).
Сложности, которые приходится преодолевать в данном случае, связаны с тем, что далеко не всегда возможно привести равносильность одного и того же преобразования однозначно: в некоторых случаях оно может оказаться, например, равносильным, в других равносильность будет нарушена [23].
Решением неравенства называется значение переменной (неизвестного), при котором неравенство превращается в правильное числовое неравенство. Например, число 5 является решением неравенства
x2 – 6х 2 – 6∙5
Решить неравенство – означает найти все его решения или доказать, что их нет. Решениями неравенства является некоторое подмножество действительных чисел.
Рассмотрим общепринятые обозначения и изображения множеств чисел (табл.2):
Решить неравенство – означает найти все его решения или доказать, что их нет. Решениями неравенства является некоторое подмножество действительных чисел.
Рассмотрим общепринятые обозначения и изображения множеств чисел (табл.2):
Таблица 2
| Название | Обозначение | Изображение | Запись в виде неравенства |
| Числовая прямая | (−∞;+∞),R |
| −∞ |
| Закрытый промежуток (отрезок) | [a;b] |
| а≤ х ≤b |
| Открытый промежуток (интервал) | (a;b) |
| а |
| Полуоткрытый промежуток | [a;b) |
| а≤ х |
| (a;b] |
| а | |
| Бесконечный промежуток (луч) | (−∞;а] |
| х ≤ а |
| (−∞;а) |
| х | |
| (а;+∞) |
| х а | |
| [а;+∞) |
| х ≥ а |
Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств. Неравенства, входящие в систему, объединяются фигурной скобкой.
Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет. Чтобы решить систему неравенств с одной переменной, надо:
отдельно решить каждое неравенство;
найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств
[22].
Основные виды решения линейных неравенств покажем схематично
(рис. 5, рис. 6):
Рис. 5. Рис.6.
Схема решения линейного Схема решения линейного
неравенства ах + b 0 неравенства ах + b 0
.
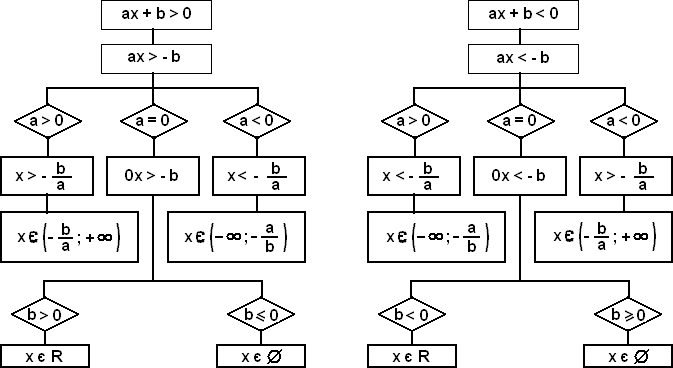
Рассмотрим алгоритмы решения неравенств и систем неравенств, рассматриваемых в курсе основной школы.
Алгоритм решения линейного неравенства.Раскрыть скобки (если нужно);
Неизвестные перенести в левую часть неравенства, известные в правую часть. (При переносе знаки перед слагаемыми изменить на противоположные «–» на «+»;«+» на «–»; знак неравенства сохраняется);
В каждой части привести подобные слагаемые, получаем неравенство вида: ax b, ax b, ax b, ax b;
Чтобы найти x, число b, стоящее в правой части разделить на коэффициент при x(a), причём, если a 0, то знак неравенства сохраняется, если a 0, то знак меняется на противоположный («» на «»; «» на
«»;«» на «»;«» на «»);
Решение изобразить на числовой прямой и ответ записать промежутком [16].
Решить первое неравенство, найти его решение;
Решить второе неравенство, найти решение второго неравенства;
Найти пересечение двух множеств значений х [26].
Рассмотреть функцию, заданную формулой y = ах² + bх + с и определить куда направлены ветви параболы (а 0 – вверх, а вниз);
Найти координаты точек пересечения параболы с осью Х, решив уравнение y = ах² + bх + с, т.е. определить нули функции.
Отметить нули функции на координатной плоскости, используя обозначения точек при решении неравенств.
Схематично построить параболу согласно описанию (см. п.1 данного алгоритма).
Записать ответ в виде промежутка(промежутков), применяя обозначения скобок [18].
тип
Записать неравенство в виде: (x–x1)(x–x2)(x–x3)…(x–xn)0;
Рассмотреть функцию, заданную формулой:
f(x)= (x–x1)(x–x2)(x–x3)…(x–xn);
Выписать нули функции: x1, x2, x3, …, xn;
Отметить нули функции на числовой прямой, используя соответствующие обозначения точек;
Отметить интервалы на числовой прямой;
Проверить знаки функции на каждом полученном интервале;
Записать ответ в виде числового промежутка(промежутков), используя соответствующие обозначения скобок.
тип
Найти область определения функции y = f(x);
Найти нули функции y = f(x);
На числовую прямую нанести область определения и нули функции. Нули функции разбивают ее область определения на промежутки, в каждом из которых функция сохраняет постоянный знак;
Найти знаки функции в полученных промежутках, вычислив значение функции в какой-либо одной точке из каждого промежутка;
Записать ответ [18].
Строим график функции y = f(x), который разбивает плоскость на две области.
Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. приближения, пересечение и объединение множеств, числовые промежутки, решение неравенств с одной переменной, решение систем квадратных и рациональных неравенств с одной переменной, а так же в блоке «Для тех, кто хочет знать больше» показана тема доказательства неравенств.
- Методические особенности изучения основных классов неравенств и их систем
В ходе изучения неравенств становится все более заметной роль общих, универсальных средств решения и исследования. Такие обобщенные средства, приемы можно разделить на три группы.
Первая группа состоит из логических методов обоснования решения. Используя эти методы (например, равносильные преобразования или логическое следование), переходят от исходных неравенств к новым. Такие переходы делаются до тех пор, пока не получаются задания, относящиеся к известным классам [26].
Вторая группа состоит из вычислительных приемов, посредством которых производятся упрощения одной из частей данного неравенства, проверка найденных корней при помощи подстановки вместо неизвестного, различные промежуточные подсчеты в т.д. [26].
В третью группу входят наглядно-графические приемы. Большинство этих приемов используют в качестве основы координатную прямую либо координатную плоскость. Использование координатной прямой позволяет решать некоторые неравенства и системы неравенств с одним неизвестным, а также неравенства с модулями. Например, прием решения систем линейных неравенств с одним неизвестным состоит в том, что на координатную прямую наносятся множества решений каждого неравенства, а потом выделяется их общая часть. Решение неравенств с модулями связывается с геометрической интерпретацией модуля разности чисел [26].
Использование координатной плоскости позволяет применить графические методы к решению и исследованию неравенств и их систем как с одним, так и с двумя неизвестными. Графические приемы эффективно применяются для изображения результатов исследования там, где чисто аналитическая запись громоздка [35]. Характерным примером служит схема, на которой приведены различные случаи решения неравенства ax² + bx + c 0, помещенная на рис.7. В результате определенной тренировки учащиеся привыкают пользоваться такой схемой, а затем ее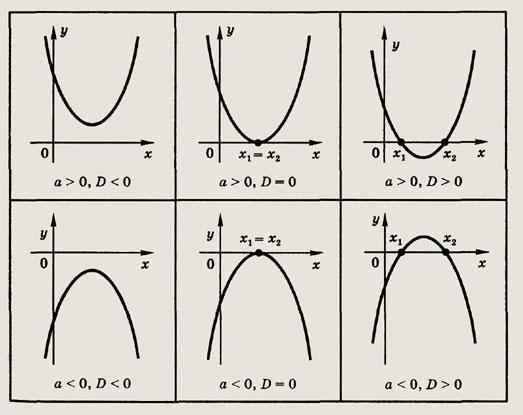 
мысленным образом.
Рис. 7.
Случаи решения неравенства ax² + bx + c 0
Классы неравенств можно разбить на две группы. Первая группа – рациональные неравенства и системы. Вторая группа – иррациональные и трансцендентные неравенства и системы (нами не рассматриваются). В состав этой группы входят иррациональные, показательные, логарифмические и тригонометрические неравенств
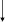
Последовательность изучения различных классов неравенств и систем различна в разных учебниках. Однако количество возможных вариантов для последовательности их введения не слишком велико – классы находятся в определенной логической зависимости друг от друга, которая предписывает порядок их появления в курсе.
Наличие такого разнообразия подходов затрудняет методическое описание, поскольку принятие того или иного пути требует различных приемов изучения материала.
Отметим ряд особенностей в изучении неравенств:
как правило, навыки решения неравенств, за исключением квадратных, формируются на более низком уровне, чем уравнений соответствующих классов;
большинство приемов решения неравенств состоит в переходе от
данного неравенства a b к уравнению а = b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Пожалуй, такого перехода не производится лишь при рассмотрении линейных неравенств, где в нем нет необходимости из-за простоты процесса решения таких неравенств. Эту особенность необходимо постоянно подчеркивать, с тем, чтобы переход к уравнениям и обратный переход превратились в основной метод решения неравенств, в старших классах он формализуется в виде «метода интервалов»;
в изучении неравенств большую роль играют наглядно-графические средства. Указанные особенности могут быть использованы для обоснования расположения материала, относящегося к неравенствам, количества заданий, необходимых для усвоения программного минимума.
Первая особенность может быть истолкована так: при выполнении одного и того же числа упражнений, техника решения неравенств какого- либо класса будет ниже, чем уравнений соответствующего класса. Следовательно, если имеется необходимость формирования прочных навыков решения неравенств, то для этого требуется большее число заданий [32].
Вторая особенность объясняет то, что темы, относящиеся к неравенствам, расположены после тем, относящихся к соответствующим классам уравнений. В соответствии с третьей особенностью изучение неравенств зависит от качества изучения функциональной линии школьного курса (построение графиков и графическое исследование функций) [32].
Перечисленные особенности показывают, что изучение предшествующего материала сильно влияет на изучение неравенств. Поэтому роль этапа синтеза в изучении неравенств особенно возрастает [20].
Из числа типов заданий, в которых проявляется прикладная роль неравенств в курсе алгебры, отметим нахождение области определения функции и исследование корней уравнений в зависимости от параметров.
Общая последовательность изучения материала линии неравенствпредставляет собой соблюдение следующих процессов [25]:
необходимо учитывать два противоположных направленных процесса, сопровождающие обучение.
Первый процесс – постепенное возрастание количества классов неравенств и приемов их решения, различных преобразований применяемых в решении. За счет увеличения объема материал как бы дробится, изучение его новых фрагментов затрудняется наличием уже изученных.
Второй процесс – установление разнообразных связей между различными классами уравнений, выявление все более общих классов, закрепление все более обобщенных типов преобразований, упрощение описания и обоснования решений.
в результате взаимодействия этих процессов изученный материал должен представляться учащимся в сравнительно компактном виде, не затрудняющем, а, наоборот, облегчающем усвоение нового. Необходимость установления такого взаимодействия обусловливает применяемые в линии уравнений и неравенств методические приемы, в частности распределение материала обучения по ступеням.
Введение каждого нового основного класса неравенств сопровождается введением новой области числовых выражений, входящих в стандартную форму записи ответа. Вместе с тем, когда материал усвоен, целесообразно изредка предлагать и такие задания, в которых могут возникать нестандартные для данного класса неравенств ответы.
Каждый из основных классов неравенств и их систем требует проведения исследования зависимости результата от коэффициентов, поскольку множества решений у заданий, входящих в один и тот же класс, могут существенно различаться. Для неравенств и их систем в качестве меры различия обычно берутся простейшие особенности геометрических фигур, изображающих их множества решений на координатной прямой или плоскости. Изредка требуется выяснить положительность или
отрицательность корней (если неизвестное одно), принадлежность решений уравнений с двумя неизвестными одной из координатных четвертей [46].
На основании изложенного материала можно сделать вывод, что отдельные вопросы методики обучения решению неравенств и их систем в школьном курсе математики освещены достаточно полно.
Несмотря на значительный положительный опыт в методике преподавания темы «Неравенства», как показывает анализ результатов тестов, контрольных, выпускных экзаменационных работ, учащиеся основной школы недостаточно полно владеют основными знаниями и умениями по решению неравенств.
ГЛАВА 2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПОФОРМИРОВАНИЮ УЧЕБНЫХ НАВЫКОВ ПРИ РЕШЕНИИ НЕРАВЕНСТВ И ИХ СИСТЕМ
Ученик обязан знать формулы решения основных типов простейших неравенств и применять их на практике; применять простейшие тождественные преобразования для приведения неравенств к стандартному виду. Данная тема выбрана мной, исходя из актуальности и сложности изучения решения неравенств. Неравенства применяются как при решении алгебраических, так и геометрических задач. Для успешного усвоения этой важной темы применяется алгоритм решения неравенств. Знания, умения, навыки решения неравенств необходимы при подготовке к ОГЭ, ЕГЭ. Неравенства встречаются на протяжении всего курса математики. С точки зрения математической логики неравенство является высказыванием. С помощью неравенства задаются основные числовые множества, на языке неравенств нередко формулируется постановка задачи во многих
приложениях математики.
Областям функционирования и возникновения понятия неравенств в алгебре соответствуют следующие основные направления раскрытия темы неравенств в школьном курсе математики [28]:
а) главным образом при изучении алгебраического метода решения задач, в том числе текстовых. Этот метод широко применяется в школьной математике.
б) математическое моделирование. Прикладное значение неравенств и их систем определяется их значимостью при данном направлении.
в) теоретико-математическая раскрывается в двух аспектах:
изучении наиболее важных классов неравенств;
изучении обобщенных понятий и методов в целом.
Использование обобщенных понятий и методов задает упорядоченное изучение линии неравенств и их систем в целом, в свою очередь эти понятия
опираются на такие основные понятия, как неравенство, равносильность, логическое следование, что имеет важное значение при изучении темы.
г) направленность на установление связей с предыдущим и последующим содержанием курса математики. Это направление тесно связано с числовой линией. Основная идея, которая реализуется в процессе установления данной взаимосвязи этих линий, – идея последовательного расширения числовой системы. Например, числовые промежутки выделяются линиями неравенств или их системами.
Обратное же влияние состоит в том, что каждая вновь введенная числовая область расширяет возможности составления и решения различных неравенств.
Процесс изучения неравенств тесно связан с функциональной линией.
Одна из важнейших связей – приложение методов к исследованию (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т.д.).
С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем.
- Пояснительная записка к элективному курсу «Неравенства и их системы в основной школе»
Программа рассчитана на 9часов. Элективный курс предназначен для повышения эффективности подготовки учащихся 9-го класса к сдаче ОГЭ.
Цель курса: совершенствовать математическую культуру и творческие способности учащихся; обобщить и систематизировать, расширить и углубить, развить умение анализировать и сопоставлять знания по теме, повысить уровень математической подготовки на основе коррекции базовых
математических знаний. Курсу отводится 1 час в неделю (вторая – третья четверть учебного года). Всего 10 часов.
Умения и навыки учащихся, формируемые курсом:навык самостоятельной работы с таблицами и справочной литературой;
составление алгоритмов решения уравнений, неравенств и систем уравнений;
умение анализировать, сравнивать, систематизировать и обобщать;
уметь решать нестандартные уравнения различными методами.
Краткость изучения материала.
Практическая значимость для учащихся.
Контрольно-самостоятельная работа.
Тематический контроль-тест.
Итоговая работа.
Подбор индивидуальных заданий осуществляется с учетом уровневой дифференциации, причем выбор делают сами ученики, оценивая свои возможности и планируя перспективу развития. Учащимся, ориентированным на выполнение заданий более высокого уровня сложности, предлагается самостоятельный подбор задач на изучаемую тему курса из дополнительной математической литературы.
Ожидаемый результат в результате прохождения курса:раскрытие способностей обучающихся;
возможность приобрести навыки самообразования;
самореализация своих возможностей;
умение обращаться к дополнительным источникам;
возможность применения полученных знаний при решении задач повышенной сложности.
| № п/п | Тема | Количе ство часов | Из них лекцио нные | практ ическ ие |
| 1 | Линейные и квадратные неравенства | 2 | 1 | 1 |
| 3 | Составление математической модели по условию задачи | 1 | 0 | 1 |
| 4 | Неравенства с одной переменной и системы неравенств | 4 | 1 | 3 |
| 5 | Итоговое занятие (контрольный тест) | 2 | 0 | 2 |
|
| Итого часов | 9 | 2 | 8 |
- Особенности обучения решению неравенств и систем неравенств в рамках элективного курса
Разработанное нами пособие представляет собой сборник заданий для повторения темы неравенств и их систем для учащихся 9-х классов основной школы. Содержит краткий теоретический материал по теме, информацию для запоминания, образцы решения типовых заданий и задания для самостоятельной работы, соответствующие требованиям государственной итоговой аттестации, итоговую работу, предназначенную для самопроверки или проверки знаний, в зависимости от плана преподавателя, а так же рекомендации учителю.
В методике даны ответы к каждому примеру для самостоятельного решения и итоговому тесту.
Цель пособия – научить выпускников основной школы ориентироваться в незнакомой математической ситуации, опираясь на основы теоретических знаний.
Если обучающийся запомнит теорию, алгоритм выполнения заданий такого типа, обратит внимание на рекомендации, ему будут посильны любые задания по данной теме [20].
В краткой форме в пособии представлены следующие теоретические сведения.
Решением неравенства называется значение переменной (неизвестного), при котором неравенство превращается в правильное числовое неравенство.
Решить неравенство – означает найти все его решения или доказать, что их нет. Решениями неравенства является некоторое подмножество действительных чисел.
Выражения вида а(в) в(а), а(в) в(а), а(в) ≥ в(а), а(в) ≤ в(а)
называются неравенствами.
Неравенства вида а(в) в(а) являются строгими неравенствами, а а(в) ≥ в(а) – нестрогими.
При решении любого неравенства необходимо привести его к более простому путем равносильных преобразований. Все произведения проводятся с учетом свойств числовых неравенств.
1. Если а в, то а − в 0; если а в, то а − в .
2. Если а в, то в а.
3. а в, в с ,то а с; а в, в с, то а с.
К двум частям неравенства можно прибавить (или вычесть) равные числа или выражения
Два неравенства одинакового смысла можно почленно складывать
Из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак первого неравенства
Если две части неравенства умножить или разделить на положительное число, то смысл (знак) неравенства не изменится.
Если две части неравенства умножить или разделить на отрицательное число, то смысл (знак) неравенства изменится на противоположный.
Неравенства вида ах + в 0 или ах + в 0 (а ≠ 0) называются
линейными неравенствами.
Практическое применение преобразований неравенств рассмотрим на примерах.
Решить неравенство:
№ 1. 3(х – 2) – 4(х + 1) х – 3) – 2
Упростим левую и правую части неравенства:
3х – 6 – 4х х – 6 – 2
–х – 10 х – 6 – 2
–3х
х – 2
3
Множество чисел х, удовлетворяющих конечному неравенству, на
числовой оси изображается лучом, а точка х = –
не принадлежит этому
3
лучу (отмечается не закрашенной точкой на числовом луче), сам луч изображен штриховкой.
− 2
3
Ответ: х∈(–
x
2 ;+∞).
3
№ 2. 3,5(х + 1) ≤ 4х − 2х−1
2
Умножим обе части неравенства на 2:
7х + 7 ≤ 8х − 2х + 1
7х − 6х ≤ 1 − 7
𝑥х≤ −6
x
−6
Ответ: х∈(– ∞;–6].
Задачи для самостоятельного решения № 1[45]:Решите неравенства: 1. −2х
2. х − 8 ≤ 3х + 6
3. 4(х + 1) − 6(2 − х) 2
4. 3х − 5(0,6х − 1)
5. 3х −9
6. −0,3х
7. 2(х + 3) ≥ 2х
8. 3(х + 2) − 2(5 − х)
9. 6х − 3(0,2х + 3) 2х
10. х+1 − 4х+1 ≤ 7−3х
4 5 10
При объяснении этой темы учителю необходимо обратить внимание на то, что два неравенства одинакового смысла нельзя вычитать друг из друга, так как в результате можно получить как верное, так и неверное неравенство.
Неравенства вида ах2 +bх + с 0 (0 ≠ 0) называются квадратными.
При решении квадратных неравенств используется свойство знакопостоянства квадратичной функции
Р(х) = ах2 + bх + с 0, а ≠ 0:
| 1. а 0,
+ – + x x1 x2 | 2. а ,
– + – x x1 x2 |
План решения квадратного неравенства:
Если D 0, трехчлен имеет два различных корня.
Найдите корни квадратного трехчлена, то есть решите квадратное уравнение вида ax2 + bx + c = 0, a≠ 0. Нанесите числа x1 и x2 на числовую ось: x
x1 x2
Поставьте знаки квадратного трехчлена в полученных интервалах соответственно знаку коэффициенту при x2.
| a 0, + – + x x1 x2 | a , – + – x x1 x2 |
Выберите интервалы:
со знаком «+», если дано неравенство ax2 + bx+ c 0
со знаком «–», если дано неравенство ax2 + bx + c 0.
Если данное неравенство нестрогое, то x1иx2принадлежат выбранным интервалам.
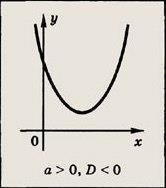Если D ,трехчлен имеет следующие решения (см. рисунок ниже):
|
|
| |
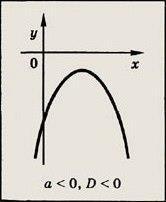
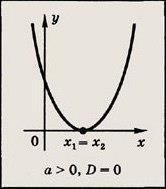Если D= 0, трехчлен имеет следующие решения (см. рисунок далее):
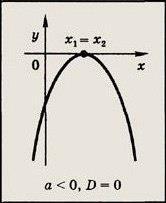
Рассмотрим примеры решения квадратных неравенств. Решите неравенства:
№ 1. (4 − 3x)(3x + 4) ≥ (2 + 9x)(x + 8)
Раскроем скобки и перенесем все члены неравенства в левую часть
16 − 9x2 − (74x + 9x2 + 16) ≥ 0.
Приведем подобные члены: −18x2 − 74x ≥ 0 ∶ (−2); 9x2 + 36x ≤ 0
(знак неравенства меняем на противоположный).
Найдем корни квадратного трехчлена:
9x2 + 36x = 0 ⇒ x1=0 , x2= -4
Нанесем корни на числовую прямую
+ – +
− 4 0
x ⇒х∈ [−4; 0 ]
Ответ: х ∈ [-4;0]
№ 2. 8х2 + 11х + 4 ≤ 0
Найдем корни квадратного трехчлена 8х2 + 11х + 4 = 0.
D = −7 ,значит уравнение не имеет действительных корней, коэффициент при x2 положительный, парабола находится в верхней полуплоскости. Значит, нет таких значений x, при которых данный трехчлен равен нулю или принимает отрицательные значения. Следовательно, решений нет.
Ответ: Ø
№ 3. 5x2 + 6x + 2 0
Аналогично предыдущему примеру, найдем корни квадратного трехчлена. Получим x1 = −1 0, нет действительных корней. Коэффициент при x2 положительный, парабола находится в верхней полуплоскости. Значит, 5x2 + 6x + 2 принимает только положительные значения. Следовательно, x – любой.
Ответ: x ∈ R.
§4. Метод интерваловЕсли левая часть неравенства с переменной y 0 (y разложена на линейные множители, то есть (x1 - x2)(x - x2) … (x - xn), (1)
то такое неравенство можно решить методом интервалов (его иногда
называют еще методом промежутков).
Метод интервалов основан на свойствах функции и заключается в следующем:
Пусть дано неравенство y 0 (y , где y имеет вид (1).
Найдем корни уравнения y = 0
k
x b1 ; x
b2
; ...; x
bn
1 2 n
1 2 n
k
k
Нанесем корни уравнения на числовую прямую
х1 х2
0 хk хk+1 хn х
Эти корни разбивают числовую прямую на n + 1 промежуток, на каждом из которых левая часть неравенства y 0 (y сохраняет знак (то есть во всех точках промежутка либо y 0, либо y , поскольку, по свойствам функции, изменить знак она может только при переходе через корни ее множителей.
y0 y 0 y 0
x1 x2
0 xk xk+1 xn x
Найдем знак левой части неравенства на каждом из полученных интервалов. Для этого на каждом из интервалов выберем какое-то значение
x = x0 и, подставив это значение в левую часть неравенства, определим ее знак (метод пробных точек).
Выберем те промежутки, где выполняется это неравенство.
Замечание 1. Неравенство y 0 (y 0) тоже можно решать методом интервалов. В этом случае корни уравнения y = 0, где y имеет вид (1), являются решениями и неравенства.
Замечание 2. В п.2, предложенного выше алгоритма, достаточно было найти знак левой части неравенства на промежутке (xn; +), а потом учесть, что она меняет знак при переходе от одного промежутка к соседнему и нарисовать «кривую знаков».
x
Там, где кривая расположена выше оси, левая часть неравенства положительна, а там, где эта кривая расположена ниже оси, левая часть неравенства отрицательна. Однако метод «кривой знаков» годится без дальнейших оговорок лишь в случае, когда все множители в левой части имеют первую степень.
Рассмотрим примеры решения неравенств методом интервалов.
№ 1. (x – 6)(x + 3) 0
Найдем корни уравнения
x 6 0
(x – 6)(х + 3)=0 x 3 0
x 6
x -3
или
Нанесем полученные корни на числовую прямую, причем, так как неравенство нестрогое и эти корни являются решениями и неравенства, изобразим их черными точками.
+ – +
–3 0 6 х
Найдем знак левой части на каждом из полученных промежутков 1) [6; +)
х = 7, y (7) = (7 – 6)(7 + 3) = 110 = 10 0 y 0;
2) [–3; 6]
x = 0, y (0) = (0 – 6)(0 + 3) = −63 = −18 y ;
3) (–; –3]
x = −4, y (–4) = (–4 – 6)(–4 + 3) = −10(–1) = 10 0 y 0.
Нашему неравенству удовлетворяют два промежутка: (–; –3] и [6; +), поэтому
Ответ: (–; –3] [6; +).
№ 2. –х2 – 2х + 48
1. Разложим левую часть неравенства на множители
–х2 – 2х + 48 = 0 х2 + 2х – 48 = 0
Для решения этого квадратного уравнения воспользуемся теоремой Виета.
x1 x2
2, x 8; x 6
x x
48; 1 2 .
1 2
Разложим квадратный трехчлен –х2 – 2х + 48 на множители:
–х2 – 2х + 48 = − (х + 8)(х – 6), таким образом имеем неравенство:
– (х + 8)(х – 6)
Умножим обе части неравенства на (–1), при этом поменяется и знак неравенства: (х + 8)(х – 6) 0
Решим его методом интервалов:
корни уравнения (х + 8)(х – 6) = 0 мы нашли: х1 = −8, х2 = 6.
нанесем их на числовую прямую
определим знак неравенства на промежутке (6; +)
х = 7, y (7) = (7 + 8)(7 – 6) = 151 = 15 0 и проведем кривую знаков. Ответ: (–; –8)(6; +).
№ 3.
x 12
5
x 4
6
2x 2
3
Приведем неравенство к виду y 0
Для этого, все члены из правой части перенесем в левую с противоположным знаком и приведем все дроби к общему знаменателю
6x 12 5x 4102x 2
0
30
Домножим обе части неравенства на 30 (так как 300, знак неравенства не изменится), раскроем скобки и приведем подобные члены
6x 2 12x 6 5x 20 20x 20 0
6x2 37x 6 0
Разложим левую часть полученного неравенства на множители
6x2 37x 6 0
x1,2 12 12
x 37 35 72 6 ; x 37 35 2 1
1 12 12
2 12
12 6
6x2 37x 6 6x 6 x 1
6
Методом интервалов решим полученное неравенство, которое равносильно первоначальному.
6(х – 6)(х –
1 )
6
Нанесем на числовую прямую корни уравнения y = 0
Найдем знак левой части на промежутке (6; +):
x = 7, y (7) = 6(7 – 6)(7 – 1 ) = 6 41 = 41 0 y 0.
6 6
Проведем кривую знаков.
6
1 ;6
Ответ: .
6
Метод интервалов применим и к неравенствам, левая часть которых – дробь, у которой числитель и знаменатель разложены на линейные множители, например, к неравенству
4x 52x 6 0
6 3xx 8
В этом случае находим значения х, которые обращают в нуль и числитель и знаменатель (то есть решаем уравнения (х – 5)(2х + 6) = 0 и
(6 – 3х)(х + 8) = 0), а затем, действуем по алгоритму приведенному выше, учитывая, что значения х, обращающие в нуль знаменатель не являются решениями неравенства (изображаем их «дырками»).
Решим записанное неравенство:
1. (х – 5)(2х + 6) = 0 х = 5 или х = −3;
(6 – 3х)(х + 8) = 0 х = 2 или х = −8.
Нанесем полученные значения х на числовую прямую
–8 –3 0 2 5 х
Определим знак левой части неравенства на интервале [5; +).
х = 6,
y (6) 4(6 5)(2 6 6)
(6 3 6)(6 8)
32 0
1214
и проведем кривую знаков.
Ответ: ;
8 3;
25;
№ 4. Найти при каких значениях х выражение имеет числовое значение
.
Так как арифметический квадратный корень вычисляется только из неотрицательного числа, то для того, чтобы выражение имело числовое
значение, нужно чтобы выполнялось неравенство 2x 10 0
5x 15
Найдем значения х, при которых это неравенство выполняется, то есть решим это неравенство. Для решения воспользуемся методом интервалов.
Решим уравнения
–2х – 10 = 0 х = 5
5х + 15 = 0 х = 3
Нанесем полученные значения на числовую прямую, найдем знак
левой части неравенства на промежутке (5; +), проведем кривую знаков.
х = 6,
y(6) 2 6 10 22 0 на (5; +) y
5 6 15 45
Решением неравенства является промежуток [3; 5).
Ответ: выражение
имеет числовое значение при 3 х
Решите квадратное неравенство (в том числе методом интервалов): 1. (х + 5)(х − 3) 0;
2. (х − 2)(х + 1) 0;
3.(х − 1)(х − 8) ≥ 0;
4.(х + 5)(х + 7) ≤ 0;
5. 2х2 ≥ 4х;
6. 3х2 ≤ 12х;
7. х2 − 16 0;
8. х2 − 9х 0;
9. х2 25;
10. х2 4;
11. х2 − 3х − 4 ≤ 0;
12. х2 + 3х − 4 ≥ 0;
13. х2 − 6х + 9 ≥ 0;
14. х2 + 10х + 25 ≤ 0;
15. −х2 + 2х − 1 ≥ 0;
16. −х2 + 4х − 4 ;
17. 4х2 + 4х + 1 0;
18. х2 − 2х + 1 ;
19. −5х2 + х − 2 0;
20. −6х2 − 2х + 1 .
При повторении этой темы учителю необходимо сделать акцент на том, что нельзя умножать и делить две части неравенства на 0 или выражение, равное 0, а так же нельзя умножать или делить (сокращать) неравенства на выражение, содержащее переменную величину, так как неизвестен знак этого выражения (и не известно, меняется или нет смысл неравенства).
Важно указать и на то, что квадратный трехчлен можно разложить на множители ах2 + bx + c = a(x − x1)(x − x2), где x1 и x2 – корни квадратного трехчлена, x ≠ 0, x ≥ 0, а затем решить его методом интервалов.
§5. Системы неравенств
Система неравенств – это несколько неравенств с одной переменной.
Решение системы неравенств – это значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство.
Рассмотрим системы линейных уравнений с одной переменной, их виды и методы решения.
Система неравенсив с одной переменной - совокупность нескольких неравенств с одной и той же переменной.
Система линейных неравенств - совокупность нескольких линейных неравенств.
Чтобы решить систему неравенств, надо каждое неравенство системы решить отдельно, а потом найти решение системы как пересечение множеств решений полученных неравенств.
№ 1. Решите системы неравенств:
{ 3х ≥ 45 .
2х + 12
Решение: после преобразований получим: { х ≥ 15.
х
Перенесем эти значения на числовую прямую. Пересечений данных множеств нет. Следовательно, решений нет.
Ответ: ∅.
Часто встречаются задания, рассматривающие двойные неравенства, например:
№ 2. Решите двойное неравенство: – 4 х
Решение: преобразуем левую и правую части неравенства, прибавив к каждой части (–2) (и к центральной части тоже), а далее разделим все части неравенства на коэффициент при неизвестном и получим:
–6 х
–2 х 1 2 Отсюда следует, что значения х∈ (–2; 1 2 ).
3 3
Ответ: х = –1 – наименьшее целое значение, х = 1 – наибольшее целое значение.
Приходится решать системы неравенств, содержащие дробные неравенства, но и здесь, путем дополнительных преобразований (приведение к общему знаменателю, умножение каждого слагаемого на общий знаменатель) учащиеся находят требуемое решение без особых затруднений.
Система неравенств может содержать не два, а три и более неравенств. Необходимо произвести с ними типичные преобразования, предусмотренные данной темой, что позволит опять прийти к стандартному ответу.
х– 4
№ 3. Решите систему неравенств: {2х + 5 .
3– х 1
Решив каждое неравенство, получим новую систему:
х
{ х .
3– х 1
Построив числовую прямую с пересечением решений данных неравенств, получим х
Ответ: x∈ (-∞;2)
Доказательство неравенств сводится к тому, что сначала преобразуется его левая или (и) правая часть, далее их сравнивают. Если полученный знак неравенства верен, данное неравенство считают доказанным.
Задания с неравенствами и их системами находят применение в геометрии. Например: оцените длину средней линии треугольника АВС, которая параллельна стороне АВ, если 10,4 АВ
При решении задачи, необходимо вспомнить формулу вычисления средней линии треугольника, далее получим новое неравенство:
10,4:2 АВ : 2
5,2 АВ : 2
Задачи для самостоятельного решения № 3 [45]: Решите системы неравенств:
;
1.
х 3{
х ≥ 7
2. {х −3 ;
х
;
3. { 2х 5−3х ≥ 9
4. { −5х ;
6х − 5 х
5. 5х 5х − 3 ;
{ −3х 2
;
6.
3х + 2 0{
5х − 3 ≤ 0
;
7.
5 − 3х ≤ 0{ 4 − х
;
8.
2х − 3 0{
4х − 7 ≤ 0
;
9.
12х − 5 ≤ 0{
3х + 14 0
10.
4х + 2 0 ;
{
3х − 6 ≤ 0
11.
5 + 2х ;
{ х − 7 ≤ 4
12.
−х 3
;
{ 2х ≤ 513. {х2 + 5х − 6 ;
−3х ≤ 12
14. {3х2 − 3х − 36 ≥ 0 .
х − 5 0
Во время прохождения этой темы учителю необходимо обратить внимание учащихся на то, что система неравенств с одной переменной может иметь как конечное, так и бесконечное множество решений, и если хотя бы одно из неравенств системы не имеет решений, то и вся система не имеет решений, а пересечение непустого и пустого множеств дает в результате пустое множество.
Вариант 1.
Решите систему неравенств: { 3х 4 .
−2х 1,8
Решите неравенство: 3х − 4 2(х + 1).
Решите неравенство: х2 − 5х − 6 ≥ 0.
При каких значениях c выражение х + 18 принимает положительные значения?
Укажите неравенство, решением которого является любое число. Запишите номер правильного ответа.
1) х2 − 86 0; 2) х2 + 86 0;
3) х2 − 86 0; 4) х2 + 86 0.
Решите систему неравенств: { (х + 2)(х − 3) 0 .
2(х + 5) − 3(х − 7)
Решите систему неравенств: {х2 + 7х + 10 0.
−21 − 7х ≤ 0
Решите систему неравенств: { х2 ≥ 81 .
х2 + 10х
Вариант 2.Решите систему неравенств:{ 2х 5 .
−3х 1,2
Решите неравенство: 6х + 1 ≤ 2х .
Решите неравенство: х2 + 3х − 4 ≥ 0 .
При каких значениях k выражение 15 − 2х принимает отрицательные значения?
Укажите неравенство, решением которого является любое число. Запишите номер правильного ответа.
1) −х2 + 93 0; 2) −х2 − 93 0;
3) −х2 + 93 0; 4) −х2 − 93 0.
Решите систему неравенств: { (х + 5)(х − 6) ≥ 0 .
6(х + 1) х − 3(2 − х)
Решите систему неравенств: {2х2 + 3х − 20 0 .
х + 5 ≥ 0
Решите систему неравенств: { х2 ≤ 16 .
х2 + 5 0
Справочные материалы представлены в виде алгоритма решения полных и неполных квадратных уравнений.
Рекомендации для учащихся включают в себя советы при выполнении заданий и повторении темы.
Учитель проверяет правильность написания самостоятельных работ учащихся с помощью ключей (ответов), представленных далее.
Ответы к заданиям для самостоятельного решения.
1. х −2 2. х ≥ −7 3. х 1 4. нет решений 5.х −3
6. х −32 7. х ≥ 8 8. любое число 9. х 1 10. х 2 11
17
Задачи для самостоятельного решения № 21.−5 х 3 2. х −1, х 2 3. х ≤ 1, х ≥ 8 4. −7 ≤ х ≤ −5
5. (−∞; 0] ∪ [2; +∞) 6. [0; 4] 7. х −4, х 4 8. 0 х 9
9. −5 х 5 10. х −2, х 2 11.−1 ≤ х ≤ 4 12. х ≤ −4, х ≥ 1
13. любое число 14. −5 15. 1 16. (−∞; 2) ∪ (2; +∞)
17. х −0,5, х −0,5 18. нет решений 19. нет решений 20. любое число
Задачи для самостоятельного решения № 3 1. х ≥ 7 2. −3 х 6,5 3. х ≤ −3 4. 0,2 х 2,5 5. х − 2
3
6. (− 2
3
; 0,6] 7. [5
3
; +∞) 8. (1 1
2
; 1 ] 9. (− 14
3
4 3; 5 ] 10. (−
12
1 ; 2]
2
Вариант 1. 1. х −0,9 2. х 6 3. х ≤ −1, х ≥ 6 4. При х −18
5. 2 6. (25; +∞) 7. [−3; −2) 8. (−10; −9]
Вариант 2. 1. х −0,3 2. х −12 3. −4 ≤ х ≤ 2 4. При х 7,5
5. 4 6. [6; +∞) 7. [−5; −4) ∪ (2,5; +∞) 8. (0; 4]
Получены следующие результаты:
Описаны методические особенности изучения основных классов неравенств в рамках обучения в школе.
Разработана программа элективного курса
«Неравенства и их системы» для учащихся 9-х классов
На основе полученных результатов исследования можно сделать вывод, что введенная методическая разработка при повторении темы
«Неравенства и их системы» за курс основной школы в рамках прохождения элективного курса демонстрирует положительный результат ее апробации.
Это демонстрирует практическую значимость выпускной квалификационной работы, материалы которой могут быть использованы учителями математики, преподающими в основном звене школы, с целью подготовки учащихся к итоговой государственной аттестации.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Алгебра: учебник для 7-х классов общеобразовательный учреждений
/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под. ред. С.А. Теляковского.–М. : Просвещение, 2008. – 240 с.
Алгебра. 7 класс: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений / А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина, Е.Е. Тульчинская; под. ред. А.Г. Мордковича.– М. : Мнемозина, 2008. – 223 с.
Алгебра: учебник для 8-х классов общеобразовательный учреждений
/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под. ред. С.А. Теляковского.–М. : Просвещение, 2005. – 238 с.
Алгебра: учебник для 8 класса общеобразовательных учреждений/ С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др. – 3-е изд.– М. : Просвещение, АО «Московские учебники», 2006. – 287 с.
Алгебра. 8 класс. В 2ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (повышенный уровень)/ А.Г. Мордкович, Н.П. Николаев. – 10-е изд., доп. – М.: Мнемозина, 2013. – 256 с.
Алгебра. 8 класс. Учебник для учащихся общеобразовательных учреждений/ Г.К. Муравин, К.С. Муравин, О.В. Муравина. – 15-е изд., стереотип. – М. : Дрофа, 2013. – 254 с.
Алгебра. 8 класс. Учебник для учащихся общеобразовательных учреждений/ Ш.А. Алимов, Ю.М. Колягин и др. – 18-е изд. – М. : Просвещение, 2011. – 255 с.
Алгебра. 8 класс. Учебник для учащихся общеобразовательных учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др. – 17-е изд. – М. : Просвещение, 2009. – 271 с.
Алгебра. 8 класс. Учебник для учащихся общеобразовательных учреждений/ Н.Я. Виленкин, А.Н. Виленкин, Г.С. Сурвилло и др. – 9-е изд., дораб. – М. : Просвещение, 2010. – 303 с.
Алгебра 8 класс: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений / А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина, Е.Е. Тульчинская; под. ред. А.Г. Мордковича.– М. : Мнемозина, 2008. – 255 с.
Алгебра: учебник для 9-х классов общеобразовательный учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под. ред. С.А. Теляковского.–М. : Просвещение, 2008. – 272 с.
Алгебра. Нестандартные задачи. Экспресс-репетитор для подготовки к ГИА. 9 класс / Г. В. Сычева, Н.Б. Гусева, В.А. Гусев – М. : Астрель, 2010. – 128 с.
Алгебра. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе. ГИА / / Кузнецова Л.В., Суворова С.Б., Бунимович Е.А., Колесникова Т.В., Рослова Л.О./М. : Просвещение, 2011 – 147 с.
Больше - меньше (неравенства множеств) / Г. П. Шалаева — М. : АСТ, Слово, 2010.– 64 с.
Вавилов В.В. Задачи по математике. Уравнения и неравенства / В.В. Вавилов. – М. : Книга по Требованию, 2012. – 237 c.
Вавилов В.В. Задачи по математике. Уравнения и неравенства. Справочное пособие / В.В. Вавилов, И.И. Мельников, С.Н. Олехник, и др. – М. : Машиностроение, 1997. – 240 с.
ГИА-9класс. Математика. Тематические тестовые задания / Л.Д. Лаппо, М.А. Попов /М. : Экзамен, 2011. – 98 с.
Гилемханов Р.Г. Об одном способе решения неравенства второй степени с одной переменной //Математика в школе. – 2014. – №8. – с. 69
Государственная итоговая аттестация выпускников 9 классов в новой форме. Математика / Кузнецова Л.В., Суворова С.Б., Бунимович Е.А., Колесникова Т.В., Рослова Л.О./М. : Интелект-Центр, ФИПИ, 2011. – 189 с.
Гусев В.А. Теория и методика обучения математике: психолого- педагогические основы / В.А. Гусев. – М. : Бином, 2013. – 456 c.
Давыдов В.В. и др. Обучение математике/ В.В. Давыдов, С.Ф. Горбов и др. – М. : Мирос, 1994. – 192 с.
Денищева Л.О. Теория и методика обучения математике в школе: Учебное пособие / Л.О. Денищева, А.Е. Захарова, И. Зубарева. – М. : Бином, 2011. – 247 c.
Денищева Л.О. Теория и методика обучения математике в школе: Учебное пособие / Л.О. Денищева, А.Е. Захарова, И. Зубарева. – М. : Бином, 2014. – 247 c.
Задачи по математике. Уравнения и неравенства / В.В. Вавилов и др. – М. : Физматлит, 2010. – 240 с.
Имранов Б. О системе изучения неравенств //Математика в школе. – 2012. – №7. – с. 38
Козловский С.Н. Методика обучения математике: Учебное пособие / С.Н. Козловский. – СПб.: Лань, 2015. – 512 с.
Кипнис И.М. Задачи на составление уравнений и неравенств: Пос. для учит-й/ И.М. Кипнис. – М. : Просвещение, 1980. – 68 с.
Левитас Г.Г. Современный урок математики. Методика преподавания/ Г.Г. Левитас. – М. : Высшая школа, 1989. – 88 с.
Математика. 9 класс. Неравенства. Системы неравенств. Экспресс- репетитор для подготовки к ГИА / Г.В. Сычева, Н.Б. Гусева, В.А. Гусев – М. : Астрель, 2012 . – 128 с.
Математика. Уравнения и неравенства. Экспресс-репетитор для подготовки к ЕГЭ / И.С. Слонимская, Л. И. Слонимский – М. : Астрель, 2010
– 160 с.
Математика. 9 класс. Экспериментальная экзаменационная работа
/ Л.Д. Лаппо, М.А. Попов /М. : Экзамен, 2011. – 74 с.
Медведева Т.В. Психолого-педагогические основы обучения математике. Теория, методика, практика / Т.В. Медведева. – М. : Бином. Лаборатория знаний, 2011. – 204 с.
Методика преподавания математики в средней школе: Общая методика: Уч. пос. для студ. пед. инст-в по спец.2104 «Математика» и 2105
«Физика» / А.М. Блох, Е.С. Канин и др. Сост. Е.С. Черкасов, А.А. Столяр. – М.: Просвещение, 1985. – 336 с.
Методика преподавания математики в средней школе: Частная методика: Уч. пос. для студ. пед. инст-в по физ-мат. спец–м/ А. Блох, В.А. Гусев, Г.В. Дорофеев и др. Сост. В.И. Мишин. – М. : Просвещение, 1987. – 416 с.
Методика преподавания математики в средней школе/ В.А. Ованесян и др. – М. : Просвещение, 1980. – 368 с.
Мордкович А.Г. Алгебра 7 класс: В двух частях. Ч. 1: Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – М. : Мнемозина, 2008. – 160 с.
Мордкович А.Г. Алгебра 7 класс: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – М. : Мнемозина, 2008. –223 с.
Мордкович А.Г. Алгебра 8 класс: В двух частях. Ч. 1: Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – М. : Мнемозина, 2008. – 215 с.
Мордкович А.Г. Алгебра 8 класс: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – М. : Мнемозина, 2008. –255 с.
Мордкович А.Г. Алгебра: учебник для 9 кл. общеобразоват. учреждений/ А.Г.Мордкович. – 4-е изд. – М. :Мнемозина, 2002. – 192 с.
Мордкович А.Г. Алгебра: задачник для 9 кл. общеобразовательных учреждений/ А.Г. Мордкович. – 4-е изд. – М. :Мнемозина, 2002. – 143 с.
Мордкович А.Г. Алгебра 9 класс: В двух частях. Ч. 1: Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – М. : Мнемозина, 2004. – 192 с.
Мордкович А.Г. Алгебра 9 класс: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская. – М. : Мнемозина, 2004. –144 с.
Никольский С.М. Алгебра: учебник для 9 кл. общеобразоват. учреждений/ С.М.Никольский. – 5-е изд.– М.: Просвещение, 2008.– 255 с.
Открытый банк заданий ОГЭ по математике 2019. – Режим доступа: http://mathege.ru/or/ege/Main. – Темы № 36–41, 48–53 (тест).
Садовничий Ю.В. ЕГЭ 2015. Математика. Решение уравнений и неравенств. Преобразование алгебраических выражений. Практикум / Ю.В. Садовничий. – М. : Экзамен, 2015. – 128 с.
Садовничий Ю.В. ЕГЭ. Практикум по математике. Решение уравнений и неравенств. Преобразование алгебраических выражений/ Ю.В. Садовничий. – М. : Экзамен, 2014. – 128 с.
Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс / Кузнецова Л.В., Бунимович Е.А., Пигарев Б.П., Суворова С.Б. – М. : Дрофа, 2010 . – 148 с.
Приложение 2. Учебное пособие для элективного курса «Неравенства и их системы »
Решением неравенства называется значение переменной (неизвестного), при котором неравенство превращается в правильное числовое неравенство.
Решить неравенство – означает найти все его решения или доказать, что их нет. Решениями неравенства является некоторое подмножество действительных чисел.
Выражения вида a(b) b(a), a(b) b(a), a(b) ≥ b(a), a(b) ≤ b(a)
называются неравенствами.
Неравенства вида a(b) b(a) являются строгими неравенствами, а a(b) ≥ b(a) – нестрогими.
При решении любого неравенства необходимо привести его к более простому путем равносильных преобразований. Все произведения проводятся с учетом свойств числовых неравенств.
§1. Свойства числовых неравенств
1. Если a b, то a − b 0; если a b, то a − b .
2. Если a b, то b a.
3. Если одно число больше другого, а третье больше второго, то первое число больше первого.
К двум частям неравенства можно прибавить (или вычесть) равные числа или выражения
Два неравенства одинакового смысла можно почленно складывать
Запомните! Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как в результате можно получить как верное, так и неверное неравенство.
Из одного неравенства можно почленно вычесть другое неравенство противоположного смысла, оставляя знак первого неравенства
Если две части неравенства умножить или разделить на положительное число, то смысл (знак) неравенства не изменится.
Если две части неравенства умножить или разделить на отрицательное число, то смысл (знак) неравенства изменится на противоположный.
Практическое применение преобразований неравенств рассмотрим на примерах.
Решить неравенство:
№ 1. 3(х–2) – 4(х+1) х–3) – 2
Упростим левую и правую части неравенства:
3х – 6 – 4х х – 6 – 2
–х – 10 х – 6 – 2
–3х
х – 2
3
Множество чисел х, удовлетворяющих конечному неравенству, на
числовой оси изображается лучом, а точка х = –
2 не принадлежит этому
3
лучу (отмечается не закрашенной точкой на числовом луче), сам луч изображен штриховкой.
− 2
3
Ответ: х∈ (–
x
2 ;+∞).
3
№ 2. 3,5(х + 1) ≤ 4х − 2х−1
2
Умножим обе части неравенства на 2:
7х + 7 ≤ 8х − 2х + 1
7х − 6х ≤ 1 − 7
х ≤ −6
−6
Ответ: х∈ (– ∞;–6].
x
§3. Квадратные неравенства Неравенства вида ax2 + bx + c 0 (a ≠ 0) называются квадратными.
При решении квадратных неравенств используется свойство знакопостоянства квадратичной функции
y = ax2 + bx + c 0 , a ≠ 0:
| 1. a 0
+ – + x x1 x2 | 2. a
– + – x x1 x2 |
План решения квадратного неравенства:
Если D 0, трехчлен имеет два различных корня.
Найдите корни квадратного трехчлена, то есть решите квадратное уравнение вида ax2 + bx + c = 0, a ≠ 0. Нанесите числа x1 и x2 на числовую ось: x
x1 x2
Поставьте знаки квадратного трехчлена в полученных интервалах соответственно знаку коэффициенту при x2.
| a 0, + – + x x1 x2 | a , – + – x x1 x2 |
Выберите интервалы:
со знаком «+», если дано неравенство ax2 + bx + c 0
со знаком «–», если дано неравенство ax2 + bx + c 0.
Если данное неравенство нестрогое, то x1 и x2 принадлежат выбранным интервалам.
Если D , трехчлен имеет следующие решения (см. рисунок ниже):
Если D = 0, трехчлен имеет следующие решения (см. рисунок ниже):
|
|
|
|
|
|
Запомните! Нельзя умножать и делить две части неравенства на 0 или выражение, равное 0.
Нельзя умножать или делить (сокращать) неравенства на выражение, содержащее переменную величину, так как неизвестен знак этого выражения (и не известно, меняется или нет смысл неравенства).
Рассмотрим примеры. Решите неравенства:
№ 1. (4 − 3x)(3x + 4) ≥ (2 + 9x)(x + 8)
Раскроем скобки и перенесем все члены неравенства в левую часть
16 − 9x2 − (74x + 9x2 + 16) ≥ 0.
Приведем подобные члены: −18x2 − 74x ≥ 0 ∶ (−2); 9x2 + 36x ≤ 0
(знак неравенства меняем на противоположный!).Найдем корни квадратного трехчлeна:
9x2 + 36x = 0 ⇒ x1 = 0
x= − 4
Нанесем корни на числовую прямую
+ – +
− 4 0
x ⇒ х∈ [− 4;0]
Ответ: х∈ [− 4;0]
№ 2. 8x2 + 11x + 4 ≤ 0
Найдем корни квадратного трехчлена 8x2 + 11x + 4 = 0. D = −7 0, значит уравнение не имеет действительных корней, коэффициент при 𝑥2 положительный, парабола находится в верхней полуплоскости. Значит, нет таких значений x, при которых данный трехчлен равен нулю или принимает отрицательные значения ⇒ решений нет.
Ответ: Ø
№ 3. 5x2 + 6x + 2 0
Аналогично предыдущему примеру, найдем корни квадратного трехчлена. Получим x1 = −1 0, нет действительных корней. Коэффициент при x2 положительный, парабола находится в верхней полуплоскости. Значит, 5x2 + 6x + 2 принимает только положительные значения ⇒
⇒ x – любой.
Ответ: x ∈ R.
Запомните! Квадратный трехчлен можно разложить на множители
ax𝟐 + bx + c = a(x − x1)(x − x2), где x1 и x2 – корни квадратного трехчлена, a ≠ 0, D ≥ 0, а затем решить его методом интервалов.
§4. Метод интервалов
Если левая часть неравенства с переменной y 0 (y разложена на линейные множители,
то такое неравенство можно решить методом интервалов (его иногда
называют еще методом промежутков).
Метод интервалов основан на свойствах функции и заключается в следующем:
Пусть дано неравенство y 0 (y , где y имеет вид (1).
Найдем корни уравнения y=0
k
x b1 ; x
b2
; ...; x
bn
1 2 n
1 2 n
k
k
Нанесем корни уравнения на числовую прямую
х1 х2
0 хk хk+1 хn х
Эти корни разбивают числовую прямую на n+1 промежуток, на каждом из которых левая часть неравенства y 0 (y сохраняет знак (то есть во всех точках промежутка либо y 0, либо y , поскольку, по свойствам функции, изменить знак она может только при переходе через корни ее множителей.
Найдем знак левой части неравенства на каждом из полученных
y 0 y 0 y 0
x1 x2
0 xk xk+1 xn x
интервалов. Для этого на каждом из интервалов выберем какое-то значение x=x0 и, подставив это значение в левую часть неравенства, определим ее знак (метод пробных точек).
Выберем те промежутки, где выполняется это неравенство. Замечание 1. Неравенство y 0 (y 0) тоже можно решать методом
интервалов. В этом случае корни уравнения y = 0, где y имеет вид (1), являются решениями и неравенства.
Замечание 2. В п.2, предложенного выше алгоритма, достаточно было найти знак левой части неравенства на промежутке (xn; +), а потом учесть, что она меняет знак при переходе от одного промежутка к соседнему и нарисовать
«кривую знаков».
x
Там, где кривая расположена выше оси, левая часть неравенства положительна, а там, где эта кривая расположена ниже оси, левая часть неравенства отрицательна. Однако метод «кривой знаков» годится без дальнейших оговорок лишь в случае, когда все множители в левой части имеют первую степень.
Рассмотрим примеры решения неравенств методом интервалов.
№ 1. (x – 6)(x + 3) 0
Найдем корни уравнения
(x – 6)(х + 3) = 0
x 6 0
x 3 0
x 6
x -3
или
Нанесем полученные корни на числовую прямую, причем, так как неравенство нестрогое и эти корни являются решениями и неравенства,
+ – +
–3 0 6 х
изобразим их черными точками.
Найдем знак левой части на каждом из полученных промежутков 1) [6; +)
х = 7, y (7) = (7 – 6)(7 + 3) = 110 = 10 0 y 0;
2) [–3; 6]
x = 0, y (0) = (0 – 6)(0 + 3) = −63 = −18 y 0;
3) (–; –3]
x = −4, y (–4) = (–4 – 6)(–4 + 3) = −10(–1) = 10 0 y 0.
4. Нашему неравенству удовлетворяют два промежутка:
(–; –3] и [6; +), поэтому
Ответ: (–; –3] [6; +).
№ 2. – х2 – 2х + 48
2. Разложим левую часть неравенства на множители
–х2 – 2х + 48 = 0 х2 + 2х – 48 = 0
Для решения этого квадратного уравнения воспользуемся теоремой Виета.
x1 x2
2,
x 8; x 6
x x
48; 1 2 .
1 2
Разложим квадратный трехчлен –х2 – 2х + 48 на множители:
–х2 – 2х + 48 = −(х + 8)(х – 6), таким образом имеем неравенство
–(х + 8)(х – 6)
Домножим обе части неравенства на (–1), при этом поменяется и знак неравенства: (х + 8)(х – 6) 0
Решим его методом интервалов:
корни уравнения (х + 8)(х – 6) = 0 мы нашли: х1 = −8, х2 = 6.
нанесем их на числовую прямую
определим знак неравенства на промежутке (6; +)
х = 7, y (7) = (7 + 8)(7 – 6) = 151 = 15 0 и проведем кривую знаков.
Ответ: (–; –8)(6; +).
№ 3.
x 12
5
x 4
6
2x 2
3
Приведем неравенство к виду y
Для этого, все члены из правой части перенесем в левую с противоположным знаком и приведем все дроби к общему знаменателю
6x 12 5x 4102x 2
0
30
Домножим обе части неравенства на 30 (так как 300, знак неравенства не изменится), раскроем скобки и приведем подобные члены
6x 2 12x 6 5x 20 20x 20 0
6x2 37x 6 0
Разложим левую часть полученного неравенства на множители
6x2 37x 6 0
x1,2 12 12
x 37 35 72 6 ; x 37 35 2 1
1 12 12
2 12
12 6
6x2 37x 6 6x 6 x 1
6
Методом интервалов решим полученное неравенство, которое равносильно первоначальному.
6(х – 6)(х –
1 )
6
Нанесем на числовую прямую корни уравнения y = 0
0 1 6 х
6
Найдем знак левой части на промежутке (6; +):
6
x = 7, y (7) = 6(7 – 6)(7 – 1 ) = 6 41 = 41 0 y 0.
6 6
Проведем кривую знаков.
1 ;6
Ответ: .
6
Метод интервалов применим и к неравенствам, левая часть которых – дробь, у которой числитель и знаменатель разложены на линейные множители, например, к неравенству
4x 52x 6 0
6 3xx 8
В этом случае находим значения х, которые обращают в нуль и числитель и знаменатель (то есть решаем уравнения (х – 5)(2х + 6) = 0 и
(6 – 3х)(х + 8) = 0), а затем, действуем по алгоритму приведенному выше, учитывая, что значения х, обращающие в нуль знаменатель не являются решениями неравенства (изображаем их «дырками»).
Решим записанное неравенство:
1. (х – 5)(2х + 6) = 0 х = 5 или х = −3;
(6 – 3х)(х + 8) = 0 х = 2 или х = −8.
Нанесем полученные значения х на числовую прямую
–8 –3 0 2 5 х
Определим знак левой части неравенства на интервале [5; +).
х = 6,
y(6) 4(6 5)(2 6 6)
(6 3 6)(6 8)
32 0
1214
и проведем кривую знаков.
Ответ: ; 8 3; 25;
№ 4. Найти при каких значениях х выражение имеет числовое значение
.
Так как арифметический квадратный корень вычисляется только из неотрицательного числа, то для того, чтобы выражение имело числовое
значение, нужно чтобы выполнялось неравенство
2x 10 0
5x 15
Найдем значения х, при которых это неравенство выполняется, то есть решим это неравенство. Для решения воспользуемся методом интервалов.
Решим уравнения
–2х – 10 = 0 х = 5
5х + 15 = 0 х = 3
Нанесем полученные значения на числовую прямую, найдем знак левой части неравенства на промежутке (5; +), проведем кривую знаков.
х = 6,
y(6) 2 6 10 22 0
на (5; +) y
5 6 15 45
Решением неравенства является промежуток [3; 5).
Ответ: выражение
имеет числовое значение при 3 х
Система неравенств – это несколько неравенств с одной переменной.
Решение системы неравенств – это значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство.
Общее решение неравенств – это множество всех решений системы неравенств.
Рассмотрим системы линейных уравнений с одной переменной, их виды и методы решения.
. (Вместо знаков ,
Частные случаи показаны в таблице 3.
Таблица 3
Возможные случаи решения систем линейных неравенств
| Системы линейных неравенств (ab) | Решение и его геометрическая иллюстрация | Пример |
| xa, xb |
x ∈ (a;+∞) |
x ∈ (3;+∞) |
| x |
x ∈ (-∞;b) |
x ∈ (-∞;2) |
| xb |
x ∈ (b;a) |
x ∈ (1;4) |
| xa, x | Решений нет
| Решений нет
|
Чтобы решить систему неравенств, надо каждое неравенство системы решить отдельно, а потом найти решение системы как пересечение множеств решений полученных неравенств.
№ 1. Решите системы неравенств:
{ 3х ≥ 45 2х + 12
Решение: после преобразований получим: { х ≥ 15
х
Перенесем эти значения на числовую прямую. Пересечений данных множеств нет ⇒ решений нет.
Ответ: Ø
Часто встречаются задания, рассматривающие двойные неравенства, например:
№ 2. Решите двойное неравенство: – 4 х
Решение: преобразуем левую и правую части неравенства, прибавив к каждой части (–2) (и к центральной части тоже), а далее разделим все части неравенства на коэффициент при неизвестном и получим:
–6 х
–2 х 1 2 Отсюда следует, что значения х ∈ (–2; 1 2 ).
3 3
Ответ: х = –1 – наименьшее целое значение, х = 1 – наибольшее целое значение.
Часто приходится решать системы неравенств, содержащие дробные неравенства, но и здесь, путем дополнительных преобразований (приведение к общему знаменателю, умножение каждого слагаемого на общий знаменатель) учащиеся находят требуемое решение без особых затруднений.
Система неравенств может содержать не два, а три и более неравенств. Необходимо произвести с ними типичные преобразования, предусмотренные данной темой, что позволит опять прийти к стандартному ответу.
х– 4
№ 3. Решите систему неравенств: {2х + 5
3– х 1
Решив каждое неравенство, получим новую систему:
х
{ х
3– х 1
Построив числовую прямую с пересечением решений данных неравенств, получим х 2.
Ответ: x ∈ (-∞;2)
Доказательство неравенств сводится к тому, что сначала преобразуется его левая или (и) правая часть, далее их сравнивают. Если полученный знак неравенства верен, данное неравенство считают доказанным.
Задания с неравенствами и их системами находят применение в геометрии. Например: оцените длину средней линии треугольника АВС, которая параллельна стороне АВ, если 10,4 АВ
При решении задачи, необходимо вспомнить формулу вычисления средней линии треугольника, далее получим новое неравенство:
10,4:2 АВ : 2
5,2 АВ : 2
Решите неравенства: 1. −2х
2. х − 8 ≤ 3х + 6
3. 4(х + 1) − 6(2 − х) 2
4. 3х − 5(0.6х − 1)
5. 3х −9
6. −0,3х
7. 2(х + 3) ≥ 2х
8. 3(х + 2) − 2(5 − х)
9. 6х − 3(0,2х + 3) 2х
10. х+1 − 4х+1 ≤ 7−3х
4 5 10
Решите квадратное неравенство (в том числе методом интервалов): 1. (х + 5)(х − 3) 0
2. (х − 2)(х + 1) 0
3. (х − 1)(х − 8) ≥ 0.
4. (х + 5)(х + 7) ≤ 0
5. 2х2 ≥ 4х
6. 3х2 ≤ 12х
7. х2 − 16 0
8. х2 − 9х 0
9. х2 25
10. х2 4
11. х2 − 3х − 4 ≤ 0
12. х2 + 3х − 4 ≥ 0
13. х2 − 6х + 9 ≥ 0
14. х2 + 10х + 25 ≤ 0
15. −х2 + 2х − 1 ≥ 0
16. −х2 + 4х − 4 0
17. 4х2 + 4х + 1 0
18. х2 − 2х + 1
19. −5х2 + х − 2 0
20. −6х2 − 2х + 1
Задачи для самостоятельного решения № 3:Решите системы неравенств:
1.
х 3{
х ≥ 7
2. {х −3
х 6,5
3. { 2х 5
−3х ≥ 9
4. { −5х
6х − 5 4х
5. 5х 5х − 3
{ −3х 2
6.
3х + 2 0{
5х − 3 ≤ 0
7.
5 − 3х ≤ 0{ 4 − х
8.
2х − 3 0{
4х − 7 ≤ 0
9.
12х − 5 ≤ 0{
3х + 14 0
10.
11.
12.
4х + 2 0
{
3х − 6 ≤ 0
5 + 2х 0
{ х − 7 ≤ 4
−х 3
{ 2х ≤ 5
13. {х2 + 5х − 6
−3х ≤ 12
14. {3х2 − 3х − 36 ≥ 0
х − 5
Вариант 1.
Решите систему неравенств: { 3х 4
−2х 1,8
Решите неравенство: 3х − 4 2(х + 1)
Решите неравенство: х2 − 5х − 6 ≥ 0
При каких значениях c выражение х + 18 принимает положительные значения?
Укажите неравенство, решением которого является любое число.
Запишите номер правильного ответа. 1) х2 − 86 0 2) х2 + 86 0
3) х2 − 86 0 4) х2 + 86 0
Решите систему неравенств: { (х + 2)(х − 3) 0
2(х + 5) − 3(х − 7)
Решите систему неравенств: {х2 + 7х + 10 0
−21 − 7х ≤ 0
Решите систему неравенств: { х2 ≥ 81
х2 + 10х
Вариант 2.Решите систему неравенств: { 2х 5
−3х 1,2
Решите неравенство: 6х + 1 ≤ 2х
Решите неравенство: х2 + 3х − 4 ≥ 0
При каких значениях х выражение 15 − 2 х принимает отрицательные значения?
Укажите неравенство, решением которого является любое число. Запишите номер правильного ответа.
1) −х2 + 93 0 2) −х2 − 93 0
3) −х2 + 93 0 4) −х2 − 93 0
Решите систему неравенств: { (х + 5)(х − 6) ≥ 0
6(х + 1) х − 3(2 − х)
Решите систему неравенств: {2х2 + 3х − 20 0
х + 5 ≥ 0
Решите систему неравенств: { х2 ≤ 16
х2 + 5х 0
Решайте сначала простые задачи, тем самым у вас останется больше времени на более сложные задания.
Внимательно читайте условие задачи, прежде чем приступить к ее выполнению!
Самая распространенная ошибка – в ответах и их записи. Выполнение пункта 2 рекомендаций поможет Вам избежать подобной ситуации.
Перед работой по данной теме рекомендуется повторить такие темы, как: решение уравнений (особое внимание уделить квадратным уравнениям), решение систем уравнений, решение неравенств и изображение этих решений на числовой прямой.
Полное квадратное уравнение
Неполные квадратные уравнения и их решение
3
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1410 руб.
2350 руб.
1380 руб.
2300 руб.
1180 руб.
1960 руб.
1570 руб.
2620 руб.
Курсы ПК и ППК для учителей!
800 руб.
4000 руб.
600 руб.
3000 руб.
800 руб.
4000 руб.
800 руб.
4000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства