Тема урока: Решение системы линейных неравенств с одной переменной
Тип урока: изучение нового материала и первичное закрепление.
Дидактическая цель: создать условия для осознания и осмысления блока новой учебной информации.
Цели: 1) Образовательная: ввести понятия: решение систем неравенств, равносильные системы неравенств и их свойства; научить применять эти понятия при решении простейших систем неравенств с одной переменной.
2) Развивающая: способствовать развитию элементов творческой, самостоятельной деятельности учащихся; развивать речь, умение мыслить, анализировать, обобщать, высказывать свои мысли четко, лаконично.
3) Воспитательная: воспитание уважительного отношения друг к другу и ответственного отношения к учебному труду.
Задачи:
- повторить теорию по теме числовые неравенства и числовые промежутки;
- привести пример задачи, которая решается системой неравенств;
- рассмотреть примеры решения систем неравенств;
- выполнить самостоятельную работу.
Формы организации учебной деятельности: - фронтальная – коллективная - индивидуальная.
Методы: объяснительно – иллюстративный.
План урока:
1. Организационный момент, мотивация, постановка цели
2. Актуализация изучения темы
3. Изучение нового материала
4. Первичное закрепление и применение нового материала
5. Выполнение самостоятельной работы
6. Домашнее задание и рекомендации по его выполнению
7. Подведение итогов урока. Рефлексия.
Ход урока:
1. Организационный момент
Неравенство может быть хорошим помощником. Только надо знать, когда к нему необходимо обратиться за помощью. На языке неравенств нередко формулируется постановка задач во многих приложениях математики. Например, многие экономические задачи сводятся к исследованию систем линейных неравенств. Поэтому важно уметь решать системы неравенств. А что же значит – «решить систему неравенств»? Это мы и разберем сегодня на уроке.
2. Актуализация знаний.
Устная работа с классом, три ученика работают по индивидуальным карточкам.
Для повторения теории темы «Неравенства и их свойства», проведем тестирование с последующей проверкой и беседой по теории данной темы. Каждое задание теста предполагает ответ «Да» - фигура ? , «Нет» - фигура ____
В результате выполнения теста должна получиться какая-то фигура.
- Верно ли утверждение: если х>2 и у>14, то х+у >16?
- Верно ли утверждение: если х>2 и у>14, то х·у<28?
- Является ли число 0 решением неравенства 3х-1<11?
- Является ли неравенство 3х+ 12>2х – 2 строгим?
- Существует ли целое число, принадлежащее промежутку [-2,5;-2,3]?
- Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число, знак неравенства не меняется?
Установить соответствие между неравенством и числовым промежутком
1. (– ∞; – 0,3)
2. (3; 18)
3. [12; + ∞)
4. (– 4; 0]
5. [4; 12]
6. [2,5; 10)
Х ≥ 12
– 4 < Х ≤ 0
Х < – 0,3
2,5 ≤ Х < 10
3 < Х < 18
4 ≤ Х ≤ 12
«Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните, почему допущена ошибка, запишите в тетрадь правильное решение.
6+2х > 8 2-3х <5
2х > 8+6 -3х <5-2
2х >14 -3х <3
х > 7 ошибка: 2х<8-6 х < -1 ошибка:х>-1
3. Изучение нового материала.
Задача: Автомобиль по горной дороге за 7 часов проезжает больше 210 км, а по шоссе за 5 часов – не более 400 км. В каких пределах может изменяться его скорость?
Составление системы неравенств по условию задачи
Постановка проблемы: требуется найти такие значения х, при которых верны оба неравенства, т.е. найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют следующую запись
{ 7х > 210,
5х ≤ 400.
- Как вы думаете, что называется решением системы неравенств?
(Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы)
- Что значит « Решить систему неравенств»?
(Решить систему неравенств– значит найти все её решения или доказать, что решений нет)
- Что надо сделать, чтобы ответить на вопрос « является ли заданное число
решением системы неравенств?»
(Подставить это число в оба неравенства системы, если получатся верные неравенства, то заданное число является решением системы неравенств, если получатся неверные неравенства, то заданное число не является решение системы неравенств)
Решить самостоятельно систему к задаче на движение автомобиля и ответить на вопрос задачи.
Сформулировать алгоритм решения систем неравенств
1. Решить каждое неравенство системы.
2. Изобразить графически решения каждого неравенства на координатной прямой.
3. Найти пересечение решений неравенств на координатной прямой.
4. Записать ответ в виде числового промежутка.
Рассмотреть примеры:
{3х-2 >25 {1-5х >11
1-х <0 6х-18 >0
Ответ: (9;+ ∞) Ответ: нет решений
4. Закрепление темы.
Работа с учебником № 1574 (2,4,6) , № 1575 (1,3,5)
5. Самостоятельная работа по вариантам (Карточки- задания для учащихся на столах)
Самостоятельная работа
Вариант 1
Решите систему неравенств:
а) { х + 3 > 2,
2x ≤ 5;
б) { х -4 > 5 – 2x,
3 – 2x < 7 + x;
Вариант 2
Решите систему неравенств:
а) { х - 1 < 0,
2x ≤ 1;
б) { х -3 > 3x - 5,
2x + 7 > 3;
6. Домашнее задание: с. 376 п. 8.6 читать, № 1574 (1,3,5), №1575 (2,4,6) доп. №1576 (1,2)
7. Подведение итогов урока (выставляются оценки)
- Проанализируйте свою работу на уроке и поставьте себе оценку «5» - все понимаю; «4»- понимаю, но есть вопросы; «?» -затрудняюсь решать системы неравенств.
Рефлексия: - Какую тему рассмотрели сегодня на уроке?
- В чем испытали затруднения?
- Над чем необходимо еще поработать?
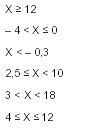
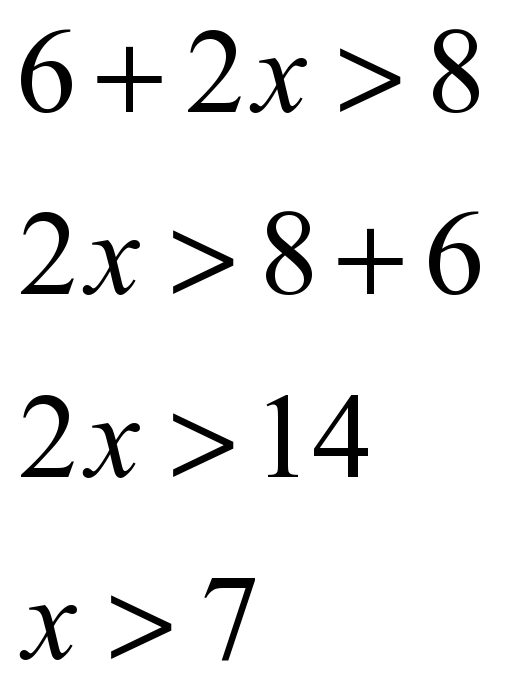
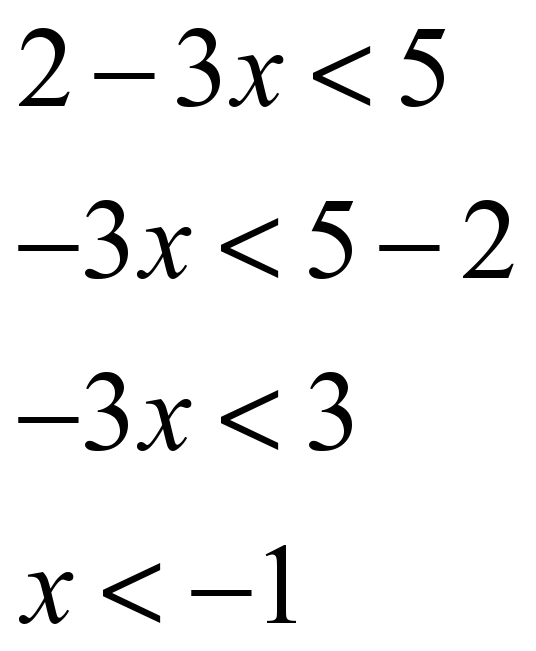 Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните, почему допущена ошибка, запишите в тетрадь правильное решение.
Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните, почему допущена ошибка, запишите в тетрадь правильное решение.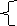 Постановка проблемы: требуется найти такие значения х, при которых верны оба неравенства, т.е. найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют следующую запись
Постановка проблемы: требуется найти такие значения х, при которых верны оба неравенства, т.е. найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют следующую запись 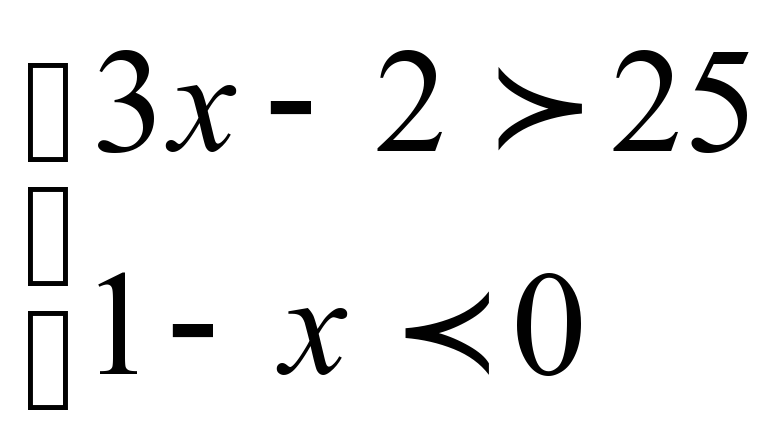 Ответ:
Ответ: 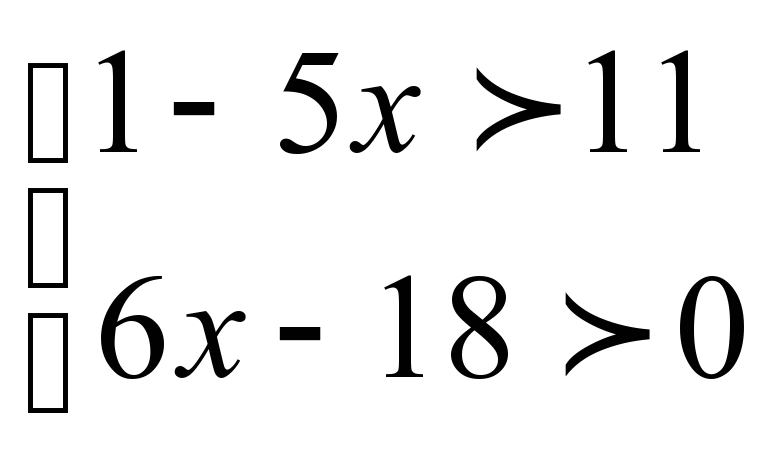 Ответ: нет решений
Ответ: нет решений